|
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
|
Fourier Series
for Open Ends
In class, we derived the normal modes for a string of length L tied down at both ends and showed that any continuous smooth function that vanished at both ends could be expanded in a Fourier series using the basis functions
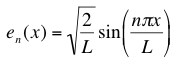 .
.
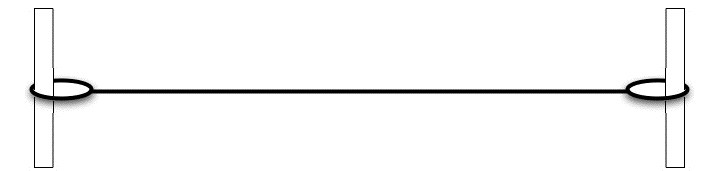
Now let's consider the physical situation of a string tied tautly to two rings and stretched between two fixed, frictionless vertical poles a distance L apart, as shown in the figure below.
- Starting from the wave equation for the string and the boundary conditions at the end, find an orthonormal set of normal modes, fn(x) that can serve as a basis for the set of motions for this string.
- If a known function f(x) is expanded in the basis fn(x), find an expression that would allow you to determine the coefficients of the expansion.
- If you have correctly determined the lowest mode of this series, you will find that it is dramatically different from any of the other solutions we have found either in this case or in the case of both ends tied down: it does not oscillate. Discuss why this mode is possible in this case but not in the ends-tied-down case and determine what its time dependence is from using the original wave equation.
This page prepared by
Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu
Last revision 13. November, 2005.


 .
.