|
ICPE NEWS
ICPE Chair Reports on Activities
and Trends on Physics Education
New ICPE Chair Members
Turning the
Challenge into Opportunities
A Physics Education Project in Africa
A Physics Problem Based on an Actual Experiment
Physics in Stamps
Physics Posters
Teaching and Learning Physics in a Cultural Context
Anamorphic Images - A Combination of Art, Physics
and Mathematics
Physics Education Conferences
Physics Education Publications
Physics Websites
|
A Physics Problem Based on an Actual Experiment
Yohtaro UENO and Toshiaki
SHIBATA
Department of Physics, Tokyo Institute of Technology
Oh-okayama, Meguro, Tokyo Japan
Most problems on physics of the university entrance
examinations in Japan are certainly appropriate for evaluating
calculating ability when only limited understanding of physics
is needed. However, it is difficult to evaluate to what extent
applicants understand basic physical ideas through these exams.
We have confirmed this via the 1999 Spring entrance examination
by including in one of such problems as above a question that
asks why there occurs a physical process for which you have calculated.
In recent days most university teachers of natural
sciences have seen a strong tendency of their students to show
less academic improvement than in the past; students are deficient
in the ability to think logically by themselves. In view of the
strong influence of entrance examinations on high school and junior
high school education in Japan, the fact that the conventional
type of problems have persisted dominantly for a long time is
without doubt a major factor that has brought about such serious
matters.
In order to get over this difficulty we have also
tried to pose problems based on or strongly related to experiments
and observations. These kinds of problems involve questions that
require understanding of basic physical ideas and are favorable
to those who have experimental and observational experience.
The problem given below is the only one that we
made by doing an experiment. We hope that this type of problems
would encourage high school teachers and students who have spent
time in doing a lot of experiments. Finally, it is worth noting
that one can complement to some extent the shortage of the conventional
type of problems by adding questions that require reasoning and
explanations.
Problem:
In order to study the force between two electric
currents running in parallel lead wires, an experiment was performed
using the apparatus as shown in Fig. 1. Although each of the lead
wires 1 (abcdef) and 2 (gh) is a part of a different closed circuit,
the remaining part of the circuit is abbreviated in Fig. 1. 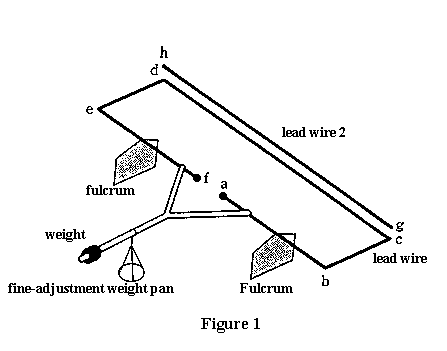 Lead wire 2 (hereafter abbreviated as LW2) is positioned
horizontally, and its length is equal to segment cd of LW1. LW1
is attached to a Y-shaped insulator between a and b between e
and f. These connected parts are supported by two insulated fulcrums
at the midpoint of segments ab and ef, so that the system is balanced.
Segments ab and ef are co-linear and serve as the axis of the
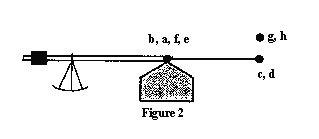
balance. (Fig. 2 shows the apparatus viewed along the axis). When
the balance is in balance, the plane of LW1 is horizontal and
cd lies directly under gh. The force exerted on segment cd of
LW1 can be measured by the adjusting the weights on the fine-adjustment
weight pan. The abbreviated parts of the circuits in Fig. 1 are
designed so that their influence on measuring the force be negligible.
The quadrilateral bcde is a rectangle where bc is 0.1[m] and cd
is 0.3[m]. Lead wire 2 (hereafter abbreviated as LW2) is positioned
horizontally, and its length is equal to segment cd of LW1. LW1
is attached to a Y-shaped insulator between a and b between e
and f. These connected parts are supported by two insulated fulcrums
at the midpoint of segments ab and ef, so that the system is balanced.
Segments ab and ef are co-linear and serve as the axis of the
balance. (Fig. 2 shows the apparatus viewed along the axis). When
the balance is in balance, the plane of LW1 is horizontal and
cd lies directly under gh. The force exerted on segment cd of
LW1 can be measured by the adjusting the weights on the fine-adjustment
weight pan. The abbreviated parts of the circuits in Fig. 1 are
designed so that their influence on measuring the force be negligible.
The quadrilateral bcde is a rectangle where bc is 0.1[m] and cd
is 0.3[m].
- We want to pass electric currents of up to
5[A] through LW1 and LW2. What is the most
 important thing we have to know for the purpose,
in addition to the electromotive force V[V] of the battery and
the electric resistance R[W ] of the lead wire?
Write also the equation which shows how it affects the electric
currents. important thing we have to know for the purpose,
in addition to the electromotive force V[V] of the battery and
the electric resistance R[W ] of the lead wire?
Write also the equation which shows how it affects the electric
currents.
- Firstly, we sent electric current I1=5[A]
in LW1 and no current in LW2, and balance the system by adjusting
the weight. Next, keeping 11=5[A], we sent electric
current I2[A] in the direction opposite to 11.
Varying the value of I2[A], we measured the force
exerted on segments cd and gh which was caused by the electric
current 12[A]. The distance between segments cd and
gh was kept at 0.01[m] all the time. The force was repulsive
and we obtained the result shown in Table 1. Plot this data
on the graph on the examination answer sheet, choosing appropriate
coordinates.
- Next, by moving LW2 upwards vertically while
keeping it horizontal, we varied distance r[m] between segments
cd and gh. Following the same steps as in (b), we measured the
force exerted on segments cd due to electric current I2[A],
while keeping I1=I2=5[A]. The results
are shown in Table 2. Plot this data on the graph on the examination
answer sheet, choosing appropriate coordinates.
- Let us denote by F[N] the force which acts
between segment cd in WL1 and segment gh in WL2. Taking into
account the principle of action and reaction of a force and
making use of plots obtained in (b) and (c), derive an equation
which expresses F[N] in terms of electric currents I1[A]
I2[A] and distance r[m]. Note that the derivation
should be logically done step by step. What is the value of
the proportionality constant in the equation?
- The proportional constant obtained in (d) turned
out to bw smaller than the value obtained by the formula applicable
to (d). let us consider the qualitative influence of each one
of the following items on the experiment. If it makes the constant
smaller, write S on the answer sheet. F it makes the constant
larger n other cases, write SL. If I has no influence, write
N.
- The electric current is passing through segments
ab and ef.
- Segments cd and gh are not sufficiently long.
- Geomagnetic fields are acting on segment
cd and gh.
- Although segments cd and gh are parallel,
they may not be completely in a vertical plane.
- The force acting between the lead wires, observed
in (b) and (c), can be regarded as working via the magnetic
flux density existing around one of the lead wires. In (d),
the equation for the force which acts between the lead wires
with r=0.3[m] was derived. Use that equation to derive an equation
which expresses the magnitude of magnetic flux density B[T]
at the position of LW2, generated by I1[A] running
ins segment cd with r[m]. Using the derived equation, obtain
the value of B[T] when I1=5[A] and r=0.01[m].
|
Table 1
|
Table 2
|
|
Electric Current I2[A]
|
Force [N]
|
Distance r [m]
|
Force =[N]
|
|
0.0
|
0.0
|
0.010
|
10 x 10-5
|
|
0.5
|
1.2 x 10-5
|
0.015
|
7.0 x 10-5
|
|
1.5
|
3.6 x 10-5
|
0.020
|
5.0 x 10-5
|
|
2.0
|
3.8x 10-5
|
0.025
|
4.2 x 10-5
|
|
2.5
|
5.6 x 10-5
|
0.30
|
3.7 x 10-5
|
|
 Lead wire 2 (hereafter abbreviated as LW2) is positioned
horizontally, and its length is equal to segment cd of LW1. LW1
is attached to a Y-shaped insulator between a and b between e
and f. These connected parts are supported by two insulated fulcrums
at the midpoint of segments ab and ef, so that the system is balanced.
Segments ab and ef are co-linear and serve as the axis of the
balance. (Fig. 2 shows the apparatus viewed along the axis). When
the balance is in balance, the plane of LW1 is horizontal and
cd lies directly under gh. The force exerted on segment cd of
LW1 can be measured by the adjusting the weights on the fine-adjustment
weight pan. The abbreviated parts of the circuits in Fig. 1 are
designed so that their influence on measuring the force be negligible.
The quadrilateral bcde is a rectangle where bc is 0.1[m] and cd
is 0.3[m].
Lead wire 2 (hereafter abbreviated as LW2) is positioned
horizontally, and its length is equal to segment cd of LW1. LW1
is attached to a Y-shaped insulator between a and b between e
and f. These connected parts are supported by two insulated fulcrums
at the midpoint of segments ab and ef, so that the system is balanced.
Segments ab and ef are co-linear and serve as the axis of the
balance. (Fig. 2 shows the apparatus viewed along the axis). When
the balance is in balance, the plane of LW1 is horizontal and
cd lies directly under gh. The force exerted on segment cd of
LW1 can be measured by the adjusting the weights on the fine-adjustment
weight pan. The abbreviated parts of the circuits in Fig. 1 are
designed so that their influence on measuring the force be negligible.
The quadrilateral bcde is a rectangle where bc is 0.1[m] and cd
is 0.3[m]. important thing we have to know for the purpose,
in addition to the electromotive force V[V] of the battery and
the electric resistance R[W ] of the lead wire?
Write also the equation which shows how it affects the electric
currents.
important thing we have to know for the purpose,
in addition to the electromotive force V[V] of the battery and
the electric resistance R[W ] of the lead wire?
Write also the equation which shows how it affects the electric
currents.