It's easy to use Newton's law to calculate the force components, but it's also easy to use Lagrangians, and this will warm you up for when we have to do the double pendulum.
We take the coordinate origin $(0,0)$ to be the point where the pivot is connected to the support. Then from the diagram, the cartesian coordinates of the mass $m$ are given by:
$$(x,y) = [L\sin\theta,-L\cos\theta]\nonumber$$
The derivatives, which will be needed later, are given by
$$[\dot x,\dot y] = [L\dot\theta\cos\theta,L\dot\theta\sin\theta]\nonumber$$
The total kinetic energy $KE$ and gravitational potential energy $PE$ is:
$$KE = \frac{1}{2} m (\dot x^2 + \dot y^2) = \frac{1}{2}mL^2\dot{\theta^2}\nonumber$$
$$PE = mgy = -mgL\cos\theta\nonumber$$
The motion is totally described by the angle $\theta$. This gives us a Langrangian:
$$\mathcal{L} = \frac{1}{2} mL^2\dot{\theta^2} + mgL\cos\theta\nonumber$$
To calculate the motion, we then solve the differential equation
$$\frac{d}{dt}\frac{\partial \mathcal{L}}{\partial \dot\theta} - \frac{\partial \mathcal{L}}{\partial\theta} = 0\nonumber$$
to get:
$$\ddot\theta = -\omega_0^2\sin\theta\label{epen}$$
where $\omega_0 \equiv g/L$ is the natural resonant frequency of oscillation.
The constants of the motion are: $$\theta(0) = \theta_0\nonumber$$ $$\dot\theta(0) = 0\nonumber$$
Equation $\ref{epen}$ cannot be solved analytically due to the non linearity of the $\sin$ function. Typically, what people do is to expand the $\sin\theta$ in powers of $\theta$ using a Taylor expansion: $$\sin\theta = \sum_{n=0}^\infty \frac{(-1)^n\theta^{2n+1}}{(2n+1)!} = \theta - \frac{1}{3!}\theta^3 + \frac{1}{5!}\theta^5 - ...\label{esin}$$ where $!$ means factorial, and $0!=1$. For small angles, $\theta\sim 0$, we can drop all but the lowest order term and get $\sin\theta\to\theta$ as $\theta\to 0$. Using this small angle approximation where the amplitude of the oscillation is small, equation $\ref{epen}$ becomes $$\ddot\theta = -\omega_0^2\theta$$ which describes simple harmonic motion, with $$\theta(t) = \theta_0\cos\omega t\nonumber$$ with initial conditions that $\theta(t=0)=\theta_0$.
The small angle approximation, however, is sometimes not appropriate, which leaves us with having to employ numerical techniques to be able to plot the motion $\theta(t). The techniques we will consider are the Euler method, the modified Euler-Cromer, and the Runge-Kutta (2nd order, RK2). They are pretty much based on the same concepts, the latter just being more accurate.
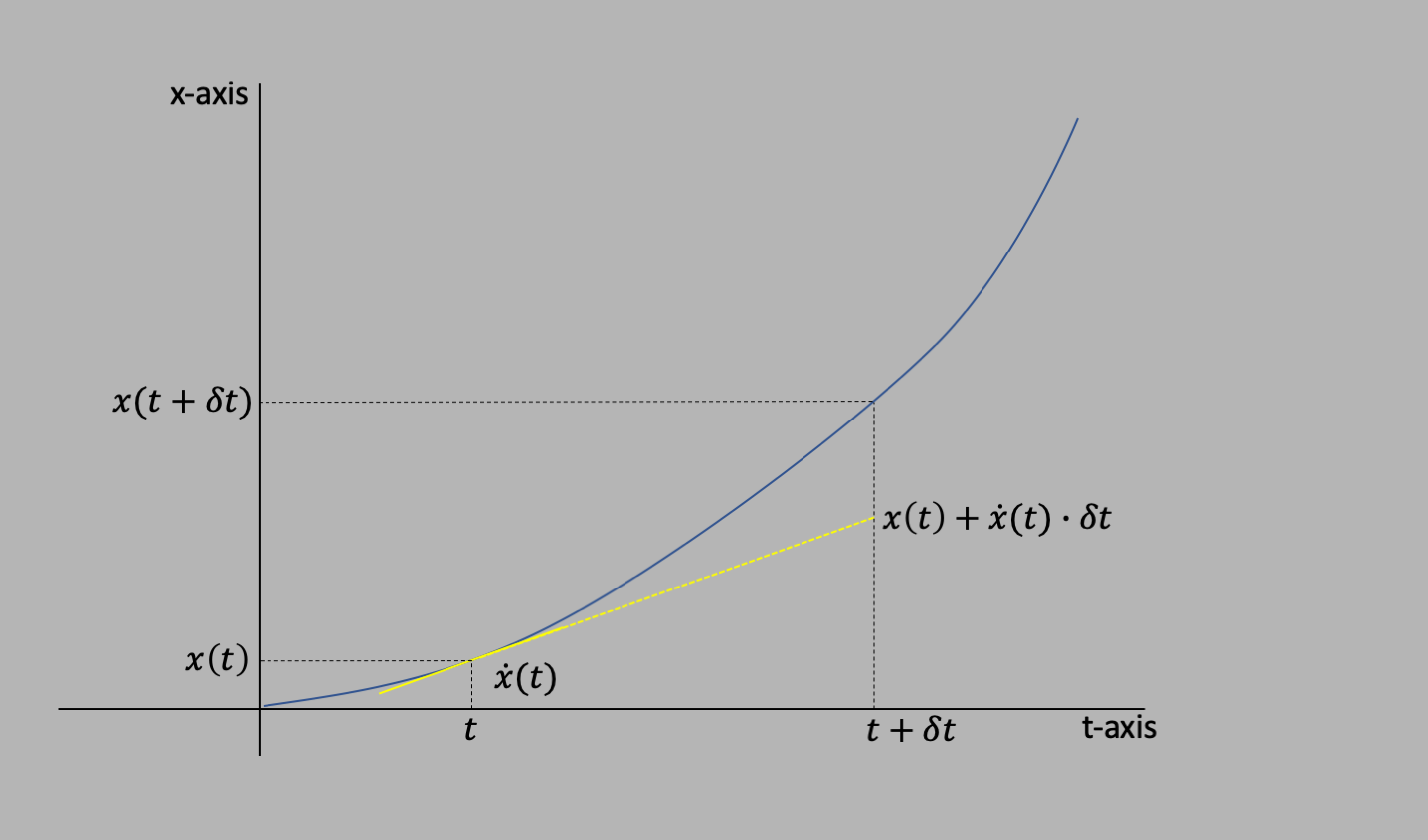
As described in the chapter on numerical integration, these 3 techniques are all based on the definition of derivatives: $$\dot x \equiv\frac{dx}{dt} = \lim_{\delta t\to 0}\frac{x(t+\delta t)-x(t)}{\delta t}\nonumber$$ If the step size in a numerical integration is small enough (that means, if you make it small enough!), we can unravel this formula and use:
$$x(t+\delta t) = x(t) + \delta t\cdot \dot x(t)\nonumber$$
This formula is the basis of the Euler approximation, and tells you how you can figure out the value of $x$ when starting from $x(t)$ after a time $\delta t$: you start at $x(t)$, and use the slope $\dot x(t)$ (slope at time $t$) to find $x(t+\delta t)$ (the value of $x$ at time $t+\delta t$). The difference in the 3 numerical integration techniques has to do with how you propagate the curve from $x(t)$ to $x(t+\delta t)$, and specifically whether you use the slope at the beginning of the interval ($\dot x(t)$), the slope at the end of the interval ($\dot x(t+\delta t)$), or the slope at the halfway time $t+\delta t$ ($\dot x(t+\frac{1}{2}\delta t)$).
You can see the situation clearly in the following plots. The solid yellow line is the slope of the $x$ v $t$ curve, and the dotted yellow line is the extrapolation from $x(t)$ to $x(t+\delta t)$ using that slope. It's clear that (for this curve, with an increasing slope) the Euler approximation underestimates extrapolation, the Euler-Cromer overestimates, and the Runge-Kutta (2) is the closest. This is because RK2 is really a second order approximation, because you need to use the Euler to get the slope at $x+\half\delta t$, so RK2 is an approximation to an approximation (aka order 2). See numerical integration for more on the details.

Note that our differential equation $\ref{epen}$ for the motion of the pendulum is 2nd order in the derivative, not first order. This is discussed in detail in the numerical integration link just mentioned, with more on the 3 different techniques: Euler; Euler-Cromer; Runge-Kutta (2).
In the simulation of the simple pendulum below, we are not making the small angle approximation that $\sin\theta\sim\theta$), and you can choose which of the 3 numerical methods discussed to see how it works. The first box below the pendulum shows the energy (somewhat arbitrary units), where the curve (color coded to the numerical integration choice) shows the energy using the values for $\dot\theta$ and $\theta$. Deviations between the curve and the yellow line give you an idea of the accuracy of the simulation, and how well the numerical method chosen works.
The 2nd plot is the "phase space" plot of $\omega\equiv\dot\theta$ vs $\theta$, and the bottom plot is just $\theta(t)$ vs $t$. The open circle (and the oscillation path) is what we would get if we used the small angle approximation $\sin\theta\sim\theta$.
| Euler Euler-Cromer Runge-Kutta |
| Energy (arbitrary units): |
All rights reserved. No part of this publication may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the publisher, except in the case of brief quotations embodied in critical reviews and certain other noncommercial uses permitted by copyright law.