Statistics is one of those subjects that has the potential to be the most obscure thing you will ever see. Yet without it, you can't really do an experiment or make an observation and come up with a meaningful conclusion.
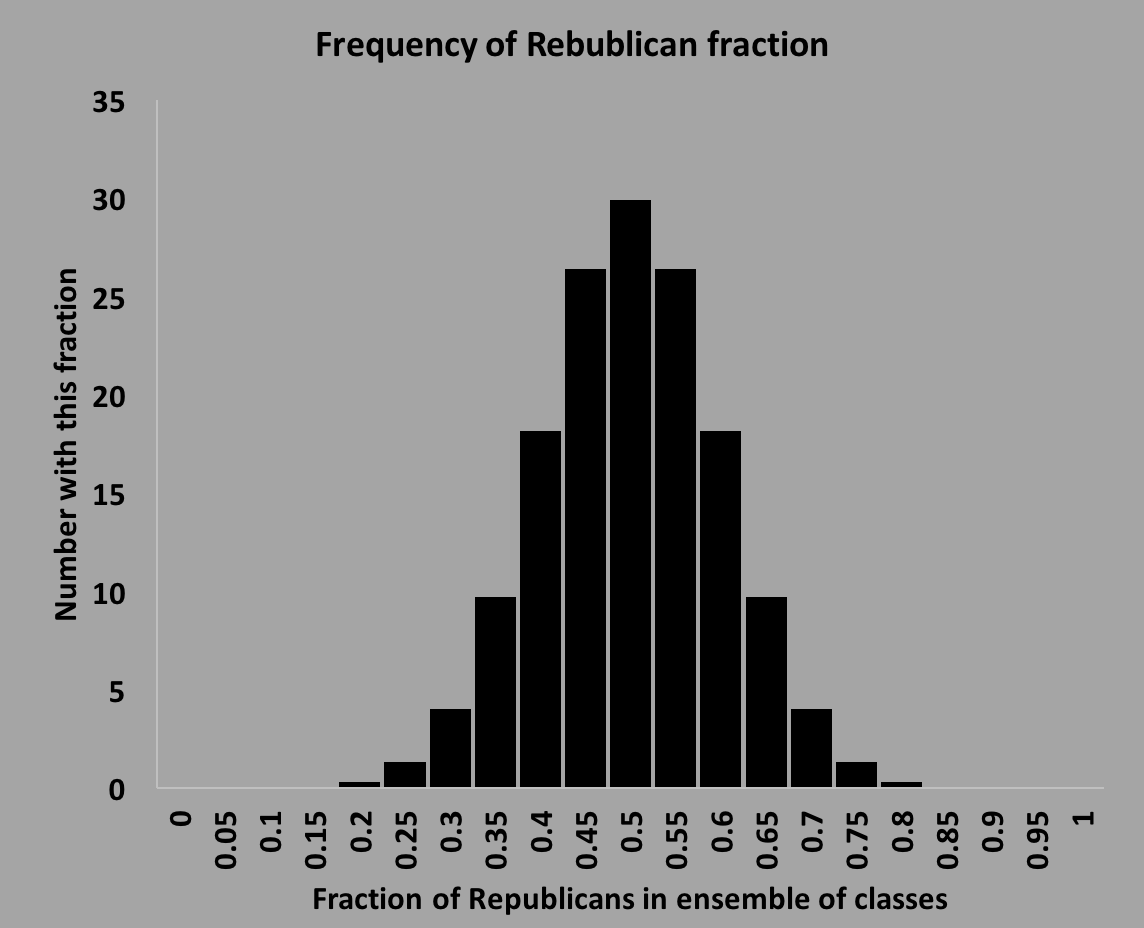
The core concept of classical statistics has to do with the idea of an ensemble of experiments, or measurements. Statistics concerns how to use the results of the ensemble to make conclusions, and to understand aspects of probability. For instance, you might want to know the probability that someone in your class is a Republican. You can count the number of Republicans, and divide by the total number of students, but that won't give you a probability - it will only give you the fraction of students in this class that are Republican. What we mean by probability is something else: if we had an ensemble of classes, and all classes are equal, then we can count the number of Republicans in each class, divide by the total to get a percentage, then make a histogram (frequency plot) of how many times we see 1%, 2%, etc. The histogram might look like the one below:

If we divide the number in each bin by the total number of classes sampled in the ensemble, we can then extract the probability distribution. If we used the fraction that had the greatest probability (the mean, or the value at the peak), when we could say that that is the probability for a class to have Republicans. Be careful here - the probability is only defined for an ensemble, and it leaves out information because it tells you nothing about how the number of Republicans are distributed. In other words you need to know now only the value at the peak, but also the shape of the distribution (a distribution that has only values at the peak will have the same mean as the one above but will have a very different distribution, and tells you a lot!).
The science of statistics tell you a lot more than just probability and probability distribution. It also tells you how to understand and characterize the twin concepts of accuracy, and precision. For example, let's start with a simple question, like "what time is it?". The answer is "12:05". Here the question is well defined, and so is the answer. But is it really? It could be 12:05, but then maybe that came from looking at one of those electric clocks that use a small AA battery that drives a small motor that drives the seconds, minute, and hour hands around. Then you read off the time by observing the position of the hands. Or maybe you are looking at some digital readout of some device that has an oscillator, counting seconds and displaying the time relative to some offset. Each of these methods ("experiments") are equally capable of delivering an answer ("result"), but you have to admit that one of them might be a lot closer to being correct than the other (more accurate). In addition, the digital readout gives a time as displayed, whereas by reading the hands of a clock you could easy be off by a minute (so the digital clock is more precise).
So here are two experiments, but the results might have very different accuracies, as well as different precision. You will find that most people in science tend to think that this added information (precision and accuracy) are important when reporting the result. Of course, in our world, knowing the time to less than a minute or two is usually not important. But in the world of science it is amazingly important, for a very simple reason: we often do experiments to find out something that we do not already know! In which case we would get a result, and compare it to what was already believed. For instance, if we drop two balls of different weight off the Tower of Pisa, and we want to see if they do hit the ground at the same time, we would make 2 measurements, $t_1$ and $t_2$, take the difference $\Delta t = t_1 - t_2$, and compare to what we expect, which is that $\Delta t=0$, also known as the "null" result ("null" meaning "nothing new"). What we want to be able to know, and to report in a systematic way, is the uncertainty in $t_1$ and $t_2$: $\delta t_1$ and $\delta t_2$. If we know these uncertainties, we can form the uncertainty in the difference, and report $\Delta t \pm \delta\Delta t$ where $\delta\Delta t$ is the uncertainty in $\Delta t$, defined in some reasonable manner (but surely a function of $\delta t_1$ and $\delta t_2$). And given these quantities, we want to understand whether the measurements yield any significant new information. And typically, we use the concepts of probability, and looking at an ensemble of measurements, to understand how to do this. Anyway the goal here is to give you some understanding and tools so that you can do just this, for this simple situation but also in general.
This is what "statistics", in the sciences, is really about: how do we characterize and understand probability, and when we make a measurement, what are the uncertainties, how do you calculate and report them, and how do you use them to understand the significance of a measurements, especially relative to the "null" hypothesis.
We start with the definitions that are most useful to know in order to understand statistics:
The mean is also sometimes called the "first moment" due to its analog with mechanics. To see this, imagine you have a collection of identical masses, $m$, you place them all at different distances from a pivot, and calculate the torque about the pivot. The picture looks like this:
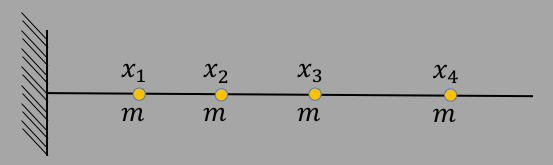
| $\tau$ | $=$ | $x_1\cdot mg + x_2\cdot mg + x_3\cdot mg + x_4\cdot mg$ |
| $=$ | $mg\cdot (x_1+x_2+x_3+x_4)$ |
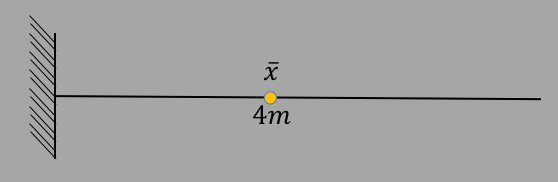
You could also place a mass that is the sum of all the other masses at some distance $\bar{x}$ from the pivot, and find $\bar{x}$ such that the torque was the same, as in the following picture:
In considering the mean, one can also consider the probability for any particular $x_i$ to occur. In the case of the average age of a group of people, when you add the ages together, you are assuming that each age is equally likely to occur, or equivalently, that one age is no more likely to occur than any other. We can calculate the probability for any age to occur in the sample easily by requiring that the sum of all probabilities should add up to 1. So in our case above, we can write $P_i$ as a shorthand for $P(x_i)$, and impose: $$\sum_{i=0}^N P_i=1\label{eprob}$$ The sum of all probabilities adds to 1 because given a set of probabilities, if they describe all possibilities, then since something has to happen, the sum of all probabilities have to add to 1. This is a key formula not only in statistics, but also in quantum mechanics.
So, if we assume that all of the $P_i$ are equal (all ages equally probable, so $P_i$ is a constant), then this sum evaluates to: $$\sum_{i=0}^N P_i=P_i\sum_{i=0}^N =P_iN=1\nonumber$$ Note that $\sum_{i=0}^N$ can be written as $\sum_{i=0}^N 1$, which is clearly just $N$.
So combining the two equations above gives us: $$P_i = \frac{1}{N}\nonumber$$ Now, we can go back to equation $\ref{emean}$ and write it a little differently: $$\bar x = \frac{1}{N}\sum_{i=0}^N x_i\nonumber=\sum_{i=0}^N \frac{1}{N}x_i =\sum_{i=0}^N P_ix_i\nonumber$$ Now we have an equation which is even more general than equation $\ref{emean}$, that tells us how to calculate the mean even if all of the measurements are not equally likely: $$\bar x = \sum_{i=0}^N P_ix_i\label{emean2}$$ This formula says something more than what's in equation \ref{emean}: it says that the mean is given by the sum of each $x_i$ "weighted" by some probability $P_i$ that tells you how likely it is that that particular $x_i$ is seen. This is very different than equation $\ref{emean}$, which tell us how to take all of the data and form the mean. In equation $\ref{emean2}$, if each of the $P_i$ are equal, then the sum is over all of the data. However, if instead we sum over all of the data that are distinctly unique, then it's an entirely different (but equally valid) equation.
To illustrate, let's calculate the $P_i$ for the two sets ${1,3,6,2,10}$ and $4,4,5,5,4$. For the first set, $P_1$ would be the probability that we see the number $1$ in the set, $P_3$ would be the probability we see the number $3$, and so on. We only have 5 numbers, and each is distinct (not repeated), so we would have $P_i \equiv P = 1/5 = 0.2$. The mean is then given by
$\bar{x}=P_1\cdot 1+P_3\cdot 3+P_6\cdot 6+P_2\cdot 2+P_{10}\cdot 10 = P\cdot (1+3+6+2+10)=0.2\cdot 22=4.4$
as before.
For the second set, we see the number $4$ occur 3 times, so $P_4=3/5=0.6$, and the number $5$ occurs twice, so $P_5=2/5=0.4$. Notice that $P_4+P_5=1$ as required. Then the mean is given by
$\bar{x}=P_4\cdot 4+P_5\cdot 5=0.6\cdot 4+0.4\cdot 5=2.4+2.0=4.4$.
Voila. This way of looking at means and variances will come in handy later.
To finish the analogy, let's go back to our example where we find the torque about a pivot point with a set of 4 masses at different locations. In that example, all of the masses were equal. Now let's imagine that they are not equal, and we have masses $m_1, m_2, m_3, m_4$ at positions $x_1, x_2, x_3, and x_4$. The torque will be given by:
$\tau=x_1\cdot m_1g + x_2\cdot m_2g + x_3\cdot m_3g + x_4\cdot m_4g$
We want to place a mass $M=m_1+m_2+m_3+m_4$ at some location $\bar x$, with resultant torque given by
$\tau=\bar xMg$
Equating the two torques give:
| $\bar x$ | $=$ | $\frac{x_1\cdot m_1 + x_2\cdot m_2 + x_3\cdot m_3 + x_4\cdot m_4} {m_1+m_2+m_3+m_4}$ |
| $=$ | $\frac{m_1}{m_1+m_2+m_3+m_4}x_1 + \frac{m_2}{m_1+m_2+m_3+m_4}x_2 + \frac{m_3}{m_1+m_2+m_3+m_4}x_3 + \frac{m_4}{m_1+m_2+m_3+m_4}x_4$ | |
| $=$ | $P_1x_1 + P_2x_2 + P_3x_3 + P_4x_4$ | |
| $=$ | $\sum P_ix_i$ |
where $P_i = m_i/(m_1+m_2+m_3+m_4)$. Here, the weights are truly weights!
Equation $\ref{emean2}$ is extremely important, especially when it comes to histograms, and what is known as "binned data". To illustrate, imagine we have a population of $N$ students, and we tabulate the age $Y_i$ of each, for example $Y_0=15.32, Y_1=12.42$, etc. Note that we use real numbers, with units in years. We can measure the mean $\bar Y$ using equation $\ref{emean}$: $$\bar{Y}=\sum_{i=0}^NY_i/N\nonumber$$ However, we also might want to look at the population distribution, to visualize the average, and how the various values are distributed about the average. To do this, we would make a histogram, which would tell us how many students have the "same" age. Histograms are all about counting, and is nothing more than a frequency distribution: how many times you see the value of some data come up. However, when we say "counting", what we mean is that we want to count the number of times we see a particular value within some range.
To make the concept of "same age" well defined, we first have to decide on the "binning", which in our example means that we need to decide on the interval of ages. For instance, we could count the number of students who are between 9 and 10, 10 and 11, 11 and 12, and so on. In this example, the bin size $\delta b$ would be 1 year. Or we could instead decide to count the number between 9 and 9.5, 9.5 and 10, and so on: bin size $\delta b=0.5$ years. This bin size is a crucial parameter in a histogram.
Then, we will want to decide on the number of bins, and the range: 0-20, or 5-15, etc. And lastly, we want to know where the bin boundaries are. For instance, if we have bins of size $\delta b=1$, then we would need to decide whether someone who is 9 years old appear in the 8-9 bin, or the 9-10 bin, or even the 9.5-10.5 bin. The standard thing to do is to decide on the bin range, and include the low edge of the bin, but not the high edge. So if the bin size is 1, and there are 10 bins, then that means the histogram will go from 0 to 10, and any age that is greater than or equal to 0, but less than 1 will fall within the 1st bin. If you have an age that is greater or equal to 2 but less than 3, it falls within the 3rd bin (2-3). And so on.
So now that we know how to specify the histogram, we can set aside some memory (an array), start the counting using the value of each each age to determine which bin it will fall in, and incrementing the corresponding array address (the bin). There is an easy way to do this: we know the bin size (call it $\delta b$), so we first take each age and divide by $\delta b$. For instance, if $\delta b=1$, and we have age $Y_i=10.42$, then $Y_i/\delta b=10.42$. If we then lop off the decimal, we have an integer, here it's 10. That's the bin number to increment! So the program would look something like this in javascript:
//
// assume all ages are in an array, called "year[i]".
// and the histogram will be in the array hist[i], initialized to 0.
//
nbins = 20;
db = 1.0;
npts = 1000; // assume all ages are in an array, called "year[i]"
for (var i = 0; i < npts; i++) {
thisbin = int(year[i]/db);
hist[thisbin] = hist[thisbin] + 1;
}
where the function "int" just truncates to an integer. (In JavaScript, you would use Math.floor().)
To illustrate, in the figure below we have 1000 ages, distributed in a classic bell curve shape with a true mean age of exactly 10 years. Above the histogram, the mean $\bar{Y}$ is calculated using equation $\ref{emean}$. The "Generate" button will simply generate a new list to histogram, and recalculate the mean. You can see how it fluctuates around the true value 10.
We would like to know how to how to calculate $\bar Y$ using the histogram bin values (and also how to characterize the fluctuation in $\bar Y$). This is where equation $\ref{emean2}$ can be used.
Back to equation $\ref{emean2}$: to find the mean using the histogram (let's call this $\bar b$, the mean from the bin values, to differentiate it from $\bar Y$, the mean as calculated using the raw data), we use equation $\ref{emean2}$ as a guide and form the following: $$\bar b = \sum_{i=1}^{N_b} P(b_i)b_i\nonumber$$ where $N_b$ is the number of bins, not the number of data points (here $N_b=20$ and $N=1000$), $b_i$ is the value of the $i$th bin (remember, the bin is the variable that has units of years), and $P(b_i)$ is the probability weight for bin $b_i$. Histograms make $P(b_i)$ easy: using the constraint described in equation $\ref{eprob}$ that all of the probabilities sum to 1, and given that the number of counts in any bin give the frequency for seeing the data in that bin range, all we have to do is divide each bin by the total number of counts (which is total number of data points generated): $$P(b_i) = \frac{N_i}{N}\nonumber$$ where $N$ is the total number, and $\sum_{i=1}^N N_i=N$.
One thing left to determine: what do we use for $b_i$? The index $i$ goes from $1$ to $N_b$, and each bin $i$ has a width $\delta_b$. We could use the left edge of the bin, or the right edge, or the middle. It is probably better to use the middle: $b_i = \delta_b(i-\half)$, and we use the $-$ sign because we are summing bins from $1$ to $N$ (if we were summing from $0$ to $N-1$ then we would use $+$). So the average $\bar Y$ will be given by: $$\bar b = \frac{\sum_{i=1}^{N_b} N_i\delta_b(i-\half)}{\sum_{i=1}^{N_b} N_i} = \frac{\delta_b}{N}\sum_{i=1}^N N_i(i-\half)\label{emeanH}$$ As a check, imagine we have a "flat" distribution, where all bins are equally likely, and so have the same number of entries. Summing the value in all bins should lead to the total number $N$, which tells us what $N_i$ is: $$N = \sum_{i=1}^{N_b} N_i = N_i\cdot N_b\nonumber$$ which gives us $N_i=N/N_b$. (Note the sum is over the number of bins, $N_b$). In this case, the probability per bin $P(b_i)=N_i/N = 1/N_b$. For instance, if we have 1000 points, and 20 bins, then each bin should hold 50 if all bins are equally likely (50x20=1000). In this case (flat distribution, constant $N_i$), our average is given by: $$\bar b = \delta_b\sum_{i=1}^{N_b} P_i(i-\half) = \frac{\delta_b}{N_b}\sum_{i=1}^{N_b} (i-\half)\nonumber$$ This is an easy thing to sum: $\sum_{i=1}^m i = m(m+1)/2$ and $\sum_{i=1}^m = m$. So our average bin will be $$\bar b = \frac{\delta_b}{N_b}\big[ \frac{N_b(N_b+1)}{2} - \half N_b \big] = \frac{N_b\delta_b}{2}\nonumber$$ In our example, if we have 20 bins each with a width of $\delta_b=1$, then the average from the perfect histogram will be $10$, which is what we would expect.
In the figure above, below the mean $\bar Y$ is shown the mean as calculated using the histogram bin contents, called $\bar b$. That the two are different is due to the fact that in making a histogram, we are throwing away some a small amount of information by binning.
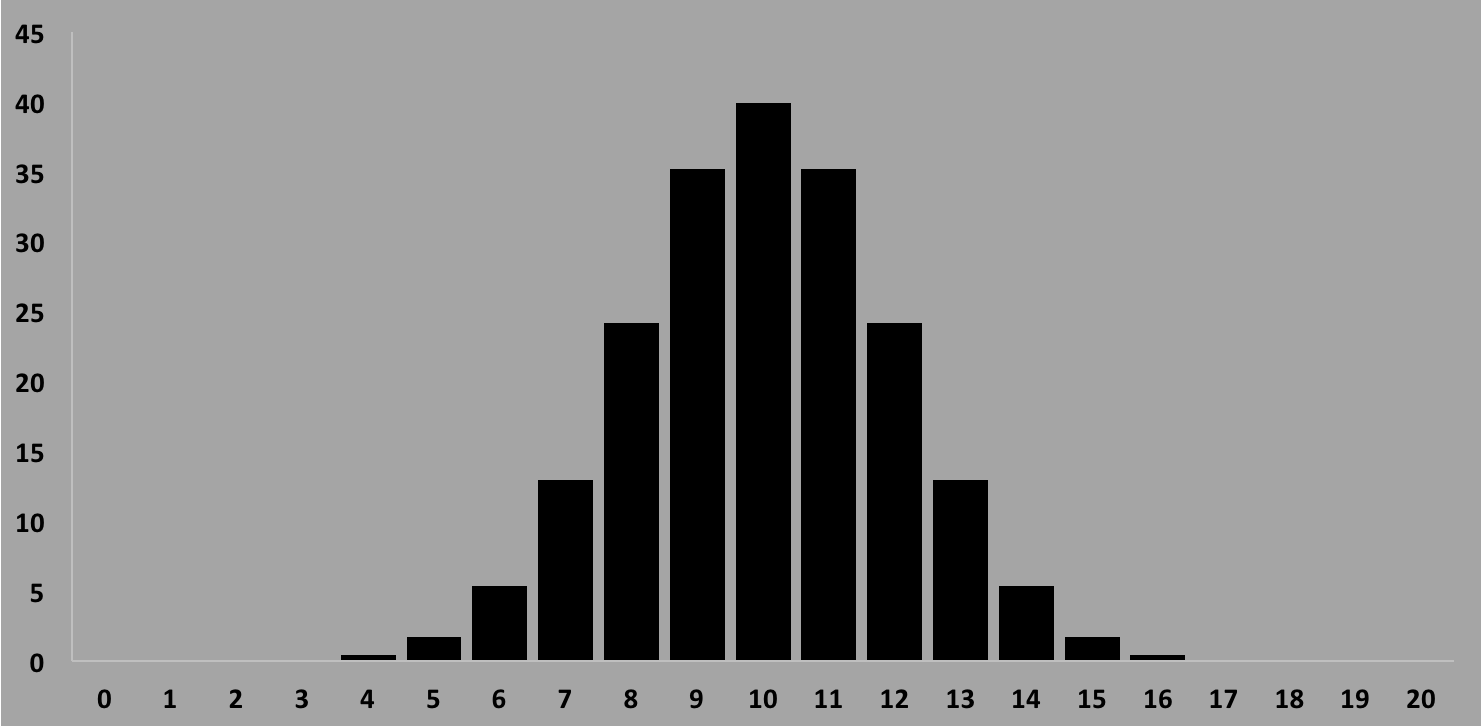
The two have the same average over the same sample size. But the distributions are very different: the probability of finding a 10 year old (age between 10 and 11) in the first distribution is around 0.2 (40/200), whereas it's around 0.1 in the second (20/200), and you are much more likely to find a 19 year old in the 2nd distribution than the first. The lesson here is that you can't just use the mean $\bar x$ to describe things completely.
This motivates some way to characterize the "spread" around the mean. The usual thing to do is to use the "variance", defined as the average of the square of the deviations from the mean: $$VAR\equiv\sigma_V^2 = \frac{\sum_{i=0}^N (x_i-\bar{x})^2}{N}\label{evar}$$ where $x_i$ is the $i$th age. If you define $d_i \equiv x_i-\bar{x}$, then the equation for the variance becomes: $$\sigma_V^2 = \frac{\sum_{i=0}^N d_i^2}{N}$$ This looks like you are taking the mean of the square of the quantity $d_i$. Since the variance $\sigma_V^2$ will have different units than $x$ (if $x$ is in meters, the variance $\sigma_V^2$ will be in meters squared), we often take the square root of $\sigma_V^2$ so that we can quote the mean and the "root mean squared" (RMS) in the same units: $$\sigma_{RMS}=\sqrt{\sigma^2}\label{erms}$$ The RMS (square root of the mean of the quantity squared) is also called the "standard deviation", and tells you something about how the values are spread about the mean.
We can take equation $\ref{evar}$ and rewrite it in the following way:
| $\sigma_V^2$ | $=$ | $\frac{1}{N}\sum_{i=0}^N (x_i-\bar{x})^2$ |
| $=$ | $\frac{1}{N}\sum_{i=0}^N (x_i^2-2\bar{x}x_i+\bar{x}^2)$ | |
| $=$ | $\frac{1}{N}\sum_{i=0}^N x_i^2 -2\frac{1}{N}\bar{x}\sum_{i=0}^N x_i + \frac{1}{N}\bar{x}^2\sum_{i=0}^N \bar{x}^2$ |
This equation is useful in computations, allowing you to run through the list of numbers once to calculate the mean, variance, and standard deviation, as shown below:
//
// assume all ages are in an array, called "year[i]".
//
//
sumy = 0;
sumx = 0;
sumx2 = 0;
for (var i = 1; i < nbins+1; i++) {
bin_i = db*(i-0.5); // we sum from 1 to nbins, db is the bin width
sumy = sumy + year[i];
sumx = sumx + bin_i
sumx2 = sumx2 + bin_i*bin_i;
}
mean = sumx/sumy;
sumx2 = sumx2/sumy;
variance = sumx2 - mean*mean;
stand_dev = sqrt(variance);
The above code assumes that the low edge of the first bin is 0. If it's not, then
you have to add that value to $bin_i$.
It is worth noting that value for $\overline{x^2}$ will always be bigger than the value $\bar{x}^2$ ($x^2$ is always positive, whereas $x$ does not have to be). So you don't have to worry about the situation where you are taking the square root of a negative number.
The following figure sums up the situation for a flat distribution with $N_b=20$ bins: the bin width $\delta_b=1/20=0.05$, the average $\bar x$ is 0.5 (halfway), and the standard deviation $\sigma_x = 1/\sqrt{12} = 0.289$. The bin boundaries to the left of the value, so for example "0.2" is the bin for $0.2\le x\lt 0.25$.

Sometimes, events (numbers) are produced from some kind of systematic process with constraints. For instance, if you randomly pulled cards out of a deck, the process limits the cards to being Ace, 2-10, J, Q, and K only. Another example, an even simpler one, might be an experiment where the answer is either yes, or no, 0 or 1. In that case, we way that the experiment is binary: 1 of 2 possible choices only. What kind of questions can you ask about the results of such an experiment? Not much, since the answer is either yes, or no. If you did the experiment $N$ times, then the number of yes results ($N_y$) plus the number of no results ($N_n$) should add to $N$: $N_n+N_y=N$. And given some number of yes and no results, you might want to ask the important question of how this compares to what we expect. Which brings you to the question of how to calculate what to expect.
To understand the answer here, let's go to a simple case where the probability of a yes ($P_y$) is equal to the probability of a no ($P_n$): $P_y=P_n$. Since probabilities sum to 1, we would have $P_y+P_n=2P_y=1$, or $P_y=P_n=\half$. This would be the case for example if you were flipping a coin.
For coin slips, we can define $P_h$ = "heads" and $P_t$ = tails. If you flipped the coin 2 times, you might want to calculate the probability that you get 2 heads in a row (call it $P_{hh}$). The way to calculate that probability is to go through all the possible outcomes, and calculate the fraction of times that that outcome exists. Each fraction will be the probability (it will add to 1!). So in an experiment with 2 coin tosses, with tosses $T_1$ and $T_2$, we could get the following combinations:
HH: $T_1=h, T_2=h$
HT: $T_1=h, T_2=t$
TH: $T_1=t, T_2=h$
TT: $T_1=t, T_2=t$
Of the 4 possibilities, HH occurs once, so the fraction of times you get 2 heads is 1/4. The fraction of times you get 2 tails is also 1/4. The fraction of times you saw one heads and one tails, without caring about which one came first, would be 2/4 (TH and HT). Another way to see this: of the 3 different combinations, the HH and TT probabilities add to 1/2, so the remaining probability (TH+HT) has to be 1/2.
This gets to a very important point: if order doesn't matter, and all you care about is the probability of getting a result, you have to keep track of the "combinatorics". More on this below.
As an interesting aside, imagine you did the same 2 flip experiment, and on the 1st flip you got a tails. What's the probability that on the 2nd flip you got a tails? You might think that it's 1/4, since after 2 flips the probability of seeing 2 tails is 1/4. Do the experiment, see what you get, but the answer will be that the probability of seeing a tails on the 2nd flip is 1/2, not 1/4. Why is this? Because the two flips are uncorrelated. And the probability of seeing a tails after a tails is not the same as the probability of seeing 2 tails in a row. The former is very specific: flip a tails, then ask for the probability of seeing another tails. The latter says: flip the coin twice, what's the probability of seeing 2 tails. So be careful with statistics. It can really cause headaches!
| $S_1$ | = | $\sum_{n=0}^\infty n^2\frac{N!}{n!(N-n)!}p^n(1-p)^{N-n}$ | |
| = | $pN\sum_{n=1}^\infty n\frac{(N-1)!}{(n-1)!(N-1-[n-1])!}p^{n-1}(1-p)^{N-1-[n-1]}$ | ||
| = | $pN\sum_{m=0}^\infty (m+1)\frac{L!}{m!(L-m)!}p^L(1-p)^{L-m}$ | ($L\equiv N-1$, $m\equiv n-1$) | |
| = | $pN[(\sum_{m=0}^\infty m\frac{L!}{m!(L-m)!}p^L(1-p)^{L-m})+1]$ | ||
| = | $pN(pL+1)$ | ||
| = | $pN(p(N-1)+1)$ | ||
| = | $pN(pN-p+1)$ | ||
| = | $pN(1-p)+(pN)^2$ |
$S_1+S_2+S_3=pN(1-p)+(pN)^2 -(pN)^2=pN(1-p)$
or $$\sigma^2=pN(1-p)=\bar{n}(1-p)\label{evarbinomial}$$ Equations $\ref{emeanbinomial}$ and $\ref{evarbinomial}$ are very useful, and tells you that the mean of a binomial distribution is just the total number of possible combinations, $N$, times the probability $p$ of any one event. In the coin experiment, $p$ is the probability of getting a heads, and $N$ is the number of coin tosses. $P(n,N)$ tells you the probability that you will see $n$ heads (and therefore $N-n$ tails), $\bar{n}=pN$ tells you the average number of heads (if $p=\half$, then $\bar{n}=N/2$), and $\sigma^2=\bar{n}(1-p)=N/4$ is the variance on the average number of heads.
It is interesting that the variance $\sigma^2$ will be equal to the mean $\bar{n}$ when $p\lt\lt 1$. This is going to be important when we next consider the Poisson distribution.
For instance, let $N=1000$ people. If we make the plot of the number of birthdays $N$
on any given day $n$, then if all days are equally likely,
$N(n)$ will look something like this:
The horizontal axis is the day of the year (1-365) and the vertical
tells you how many times we found a person with a birthday at that day.
We can see right away that it's much more likely that we see something
between 1 and 3 counts than that we see something between 8 and 10 counts.
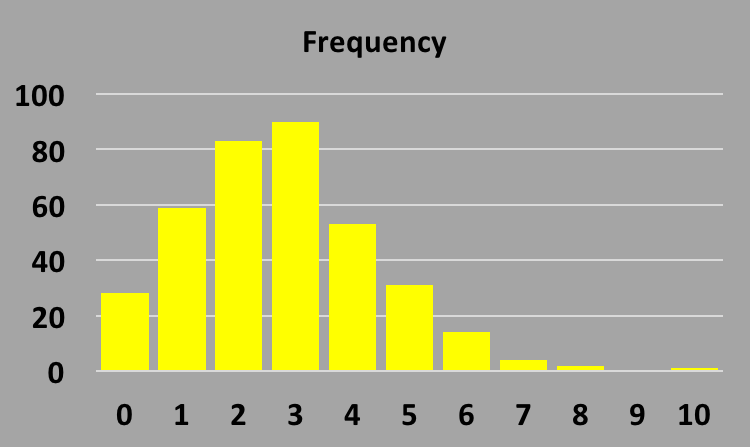
You might then want to make a histogram of the distribution of counts (how many days had 0 counts,
how many had 1, etc), called the "frequency".
In the above plot, it looks like no day had more than 10 counts, so our
frequency histogram will be from 0 to 10. It will look like this:
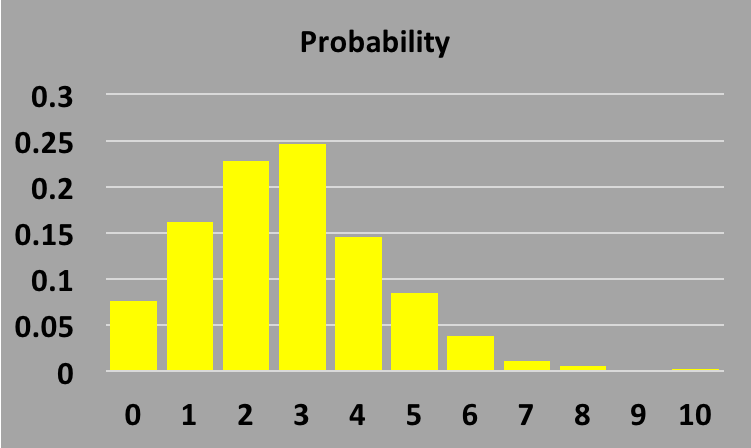
To turn our frequency histogram into a probability distribution, all we have to do is
divide each bin by the total number in the sample, which in this case is 1000
(if you sum over all the bin contents in the frequency histogram, you will get 1000
since the x axis tells you the number of days that had 0, 1, 2, etc birthdays, and
you are summing over all possible days).
The result is shown next:
To understand the shape of this probability distribution,
let's formulate the problem slowly.
We are asking each person from a sample
of $N$ people for a date corresponding to their birthday. Each answer has
a probability $p$, and since all dates are equally likely if there is no
bias, then the probability for any given date coming up will be given by $p=1/365$.
This "stream" of 1000 is no different than the "stream"
of 1000 coin tosses, each being either heads or tails. However, the difference
is that for the coin tosses, there are 2 possible outcomes, while for
the birthday experiment, there are 365.
If we ask $N$ people for their birthday, and want to predict the number of
people who have the same birthday as Mozart (January 27), then after asking
all $N$ people ($N$ samples), the
the answer will be that on average, there will be $N/365$ with that
particular birthday. If $N=365$, then
on average there will be only 1 person out of a sample of $365$ that have that
particular birthday.
Now, let's consider how to measure the probability that in a sample of $N$
people, that at least 2 of them have the same birthday as Mozart. That's equivalent
to looking at figure 1, finding the right bin (the one that
corresponds to Jan 27), and running countless experiments with $N$ people to see
how many times you get at least 2 entries. The probability will be given by
that number divided by the number of times you've tried.
To calculate what you would expect for that probability, let's start with some
small number of people, say $N=5$, and calculate the probability that we have
0, 1, 2, 3, 4, or 5 with that particular birthday (call these probabilities
$P(0)$, $P(1)$, $P(2)$, $P(3)$, $P(4)$, and $P(5)$):
The easiest way to solve this is to use the property
that probability distributions are normalized to 1:
P(at least 2 people having the same birthday) = 1 - P(no two people have the same birthday),
because the latter probability, that no two people have the same birthday, is easier
to calculate!
To start, let's take 2 people in the room. The first person will have some birthday
(it doesn't matter what the date is), so the probability that they both have the same
birthday is just the probability that the 2nd person have a birthday on
that particular date, which is $1/365$, if of courseall birthdays are equally likely.
Then the probability that they do not
share the same birthday will be $p_2=1-1/365-364/365$.
Now, introduce the 3rd person. If these first two do not have the same
birthday, then there are 363 days left for the 3rd person, so the probability that
that person does not have either of the 1st 2 birthdays will be given by the
number of possible dates left, $363$, divided by all possible dates, $365$,
or $p_3=363/365$. Then the joint probability is given by $p_2\cdot p_3$, since
we want birthday 1 not equal to birthday 2 AND birthday 3 not equal to
both 1 and 2. If we have 4 people, then then $p_4=362/365$ (3 dates are eliminated
due to 1, 2, and 3), and the joint probability will be given by $p_2\cdot p_3\cdot p_4$.
We can now extend this to an unknown number of people, $N$:
$$P(N) \equiv p_2\cdot p_3\cdot ... \cdot p_N
= \frac{364}{365}\cdot\frac{363}{365}\cdot\frac{362}{365} ... \cdot\frac{365-(N-1)}{365}\nonumber$$.
We can rewrite this as
$$P(N) = \frac{365\cdot 364\cdot 363 \cdot 362 \cdot ... \cdot 365-(N-1)}{365^N}\nonumber$$
This is the probability that for $N$ people, no two share the same birthday. The
probability of having 2 people share the same bithrday will be $1-P(N)$.
The figure below shows a plot of $P(N)$ vs $N$. You can see that for $N=23$, the
probability just barely exceeds $50\%$. This is perhaps a surprisingly small number,
however it's all due to the combinatorics: as you add people, you increase the
number of ways (the combinatorics) for $2$ out of $N$ to share the same birthday.
We can start with a single die, and roll it $N$ times. If each face is equally
likely to show up, then the probability $p(n)$ for seeing face $n$ appear will
be independent of which face: $p(n)=1/6$.
What we want to do is to calculate the following quantities after $N$ rolls:
When you roll the die $N$ times, you will be looking at a stream of numbers, each with
$M=6$ different possible values, and you want to know the probability that we see face
$n$ appear $m$ times. For example, say you roll the dice 5 times ($N=5$) and ask
for the probability that you should see face 1 appear $m=2$ times. As usual,
you can calculate these probabilities by adding up the number of different ways
something can be seen, and multiplying by the probability of seeing just that
thing. So for $m=2$, we could
see face 1 on trial 1, and then on trial 2,3,4,5, or 6.
Or, we could see some other face on trial 1, see face
1 on trial 2, and then on 3,4,5, or 6. And so on.
If you add up all possible combinations, you will get 5 (1 shows up the first
time) plus 4 (2nd), plus 3 + 2 + 1 (face 1 shows up on trial 5 and 6). So there are
5+4+3+2+1=15 ways to see face 1 show up twice. This is exactly what the
combinatorics part of the binomial distribution calculates for you, the number
of ways you can take $M=6$ things and arrange it so you see $m=2$ of them:
$$\frac{M!}{m!(M-m)!}=\frac{6!}{2!(6-2)!}=
\frac{6\cdot 5\cdot 4\cdot 3\cdot 2}{2(4\cdot 3\cdot 2)}=15\nonumber$$
To calculate the probability of seeing face $n=1$ show up $m=2$ times, we would need to
multiply by the probability of seeing face 1 showing up twice, and any other face
showing up 4 times, which would be given by
$p^2(1-p)^4$. Putting this together gives you the binomial probability
distribution $P_n(M,m)$, where $M$ is the number of different die in the
set ($M=6$), and $m$ is the number of times you would see face $n=1$:
$$P_1(m,M)=\frac{M!}{m!(M-m)!}p_1^m(1-p_1)^{M-m}\nonumber$$
Since all faces are equally likely, you can drop the subscript (here it's $n=1$),
and just write
the probability of seeing any of the faces snow up $m$ times is:
$$P(m,M)=\frac{M!}{m!(M-m)!}p^m(1-p)^{M-m}\nonumber$$
where $p=1/6$.
Since we know that the mean and variance of a binomial distribution will be given by
equations $\ref{emeanbinomial}$ and $\ref{evarbinomial}$, we can write that
So in our case here, we have the following conditions:
With these approximations, the binomial distribution then goes to:
$$P(n,N)\to \frac{\mu^ne^{-\mu}}{n!}\nonumber$$
as $n/N\to 0$, $N\lt\lt 1/p^2$, and $p\lt\lt 1$, and the definition $\mu\equiv Np$ is the mean.
This is called the Poisson distribution, and is one of the more important distributions
in science (up there with the binomial, and gaussian).
Why the poisson has only 1 parameter $\mu$ instead of the 2 parameters $p$ and $N$
for the binomial is because of the limiting condition: $p$ is very small, $N$ is
very large, but the product $\mu=pN$ is finite. Also, if the variance of the binomial
distribution is given by equation $\ref{evarbinomial}$, then in the limit of $p\to 0$,
then $Np(1-p)\to Np = \mu$ so the variance of the Poisson will be given by $\sigma^2 = \mu$,
and there really is only 1 free parameter ($\mu$).
So the poisson distribution is:
$$P(n,\mu)= \frac{\mu^ne^{-\mu}}{n!}\label{epoisson}$$
and the mean and RMS values are:
$$\mu = Np\nonumber\label{mupoisson}$$
$$\sigma_{RMS}=\sqrt{\mu}\label{vpoisson}$$
For this to be a real distribution, we would want $\sum P(n,\mu)=1$, and this is
the case (in the sum, the factor $e^{-\mu}$ factors out, leaving a sum over
$\mu^n/n!$, which is the expansion for $e^{+\mu}$).
The physical significance of these limits is interesting. For an experiment like
the birthday experiment, it describes a situation with a very small probability $p$
but a large number of trials compared to the combinations ($n\lt\lt N$). For something
like a radioactivity experiment, where you count the number of disintegrations in some
time window, the poisson also applies, since the limiting conditions means that the
probaiblity for any given particle of the sample to decay is small, and
number of counts in any particular time window will be small as well.
In the following plot, you can change the mean value $\mu$ and see the shape of the poisson
distribution $P(n,\mu)$. Notice how the distribution becomes more symmetric as $\mu$ gets
larger.
The poisson distribution is over discrete values for $n$. However, as $\mu$ gets
larger, the term $e^{-\mu}$ sends the probability to 0 except in the region near $n\sim\mu$
(play with the poisson distribution above, driving $\mu$ up). To see this more explicitly,
we can use Stirling's formula for the factorial:
$$n!\to x! \to \sqrt{2\pi x}e^{-x}x^x\label{estirling}$$
Substituting, we have
$$P(n,\mu)= \frac{\mu^ne^{-\mu}}{n!}\to\frac{\mu^ne^{-\mu}}{\sqrt{2\pi n}e^{-n}n^n}
= \frac {e^{-(\mu-n)}} {\sqrt{2\pi n}} \Big(\frac {\mu}{n}\Big)^n \nonumber$$
Now that we have an equation that substitutes for the integer $n$, we can consider the
poisson as a probability over a continuous variable $x$ instead of $n$. This will be true
when $\mu \gt\gt 1$.
This allows us to write the poisson distribution as
$$P(x,\mu)= \frac{\mu^xe^{-\mu}}{x!}\label{epoissonx}$$
Note that even though we derived the poisson starting with the binomial, the poisson can
also be derived from first principles for counting experiments where the numbers counted
are independent of each other (for instance, the number of photons from radioactive decay,
or the number of people in line at the grocery store), and the average rate is constant (and
so you are just seeing fluctuations about the average).
To derive the poisson distribution from first principles, we define
define $\lambda$ as the rate for something to occur per unit time, and break up
time into intervals of length $\dt$, so that after a time $t$ there will be
$N$ intervals ($t=N\dt$). The probability that something happens in any interval will
be given by $P=\lambda\dt$, so the probabilty that nothing happens in the
interval will be given by $1-\lambda\dt$. To calculate the probability that
nothing happens after $N$ intervals (at a time $t$ relative to $t=0$), we would
just multiply the probabilities for all intervals together, and since the occurance
is independent of the interval, we would get
$$P(0,t)=(1-\lambda\dt)^N\nonumber$$
If we want to take the limit as $\dt\to 0$, that means $N\to\infty$. To do this properly
you use the Taylor expansion, and assume $N\gt\gt 1$, and this gives the well-known formula
for the exponential:
$$P(0,t) = e^{-\lambda t}\nonumber$$
The probability that the event happens at some time is what we want to calculate: $P(t)$.
But we are talking about intervals, so the probability for the event to happen in a time
interval between $t$ and $t+\dt$ will be given by the probability that it did not
happen up until time $t$ ($e^{-\lambda t}$) times the probability that it happened in
the next interval $\lambda\dt$, or
$$P(t)\dt = e^{-\lambda t}\lambda\dt\nonumber$$
Therefore, we have calculated that $P(t) = \lambda e^{-\lambda t}$, and we are almost there,
since what we really want to calculate is the probability that after some time $t+\dt$, we will
have seen $n$ events. This is where the combinatorics
come in: you could see $n-1$ events have happened before $t$ and 1 in the next interval
$\dt$, or $n-2$ before and 2 in $\dt$, etc. After some algebra and logic, one can show that
the probability for seeing $n$ events after a time $t$ will be given by the poisson distribution:
$$P(t) = e^{-\lambda t}\frac{\lambda t}{n!}\nonumber$$
The Gaussian and the Poisson distributions are very similar. In the plot below,
the Poisson is drawn in red and the Gaussian in yellow. The mean is the same for
both, and the width of the gaussian will be given by $\sigma = \sqrt{\mu}$. As you
can see, they are similar, however the poisson variance for the gaussian gives you
a slightly wider function, showing that $\sigma = \sqrt{\mu}$ is not true for the gaussian.
Instead of deriving the gaussian starting with the binomial, or poisson, there's another
way to do it, and this will help you
to appreciate the importance of the gaussian. We start with a rather
simple and interesting problem: consider a variable $x$, distributed in some
random way. If you made a histogram of $x$ and normalize to 1, you will see the
probability distribution function $P(x)$. In this example,
we do not have to specify $P(x)$: it could be
totally random, in which case $P(x)=$constant, or it could have some totally weird
shape. The key thing is that the shape is irrelevant. Next, we generate a large
number of $x_i$ according to $P(x)$. Let's start with a probability distribution
in which $x_i$ is a random number, and so $P(x)$ is constant, or "flat".
In the world of computer programming, there are always built-in
functions that generate random numbers between 0 and 1, so each $x_i$ would be some
random number in that interval. Next, we take all of these $x_i$ and form an average
over $N$ of them, and call this average $X_N$:
$$X_N = \frac{1}{N}\sum_{i=1}^N x_i\nonumber$$
For instance, if $N=10$, and the $x_i$ are random numbers "flat" over the interval between
0 and 1, then the probability of any particular $x_i$ value seen is the same for all $x_i$,
the average $X_N$ would also be a number between 0 and 1. If we take numerous numbers
$x_i$ and form lots of different $X_N$ averages, and then
make a histogram of $X_N$, we could see the probability distribution $P(X_N)$.
We might expect the average $X_N$ to be near 0.5, however
what would you expect for the distribution of $X_N$? The answer is surprising:
$P(X_N)$ turns out to be a gaussian!
In the histogram below, you can see a distribution of random numbers. It is "flat",
but of course there are fluctuations, so the number in each histogram bin will fluctuate
somewhat.
However the more numbers you generate, the "flatter"
the distribution becomes, and you can try this by changing the box below
with the "# to generate# (call this $N_{tot}$)
and hitting the "Regenerate" button. The "# of bins in histogram:" (call this
$N_b$) is used by the code
to make the histogram, so you can change that as well and see how the "flatness" changes.
The number of entries in each bin will fluctuate around the mean for each bin,
given by $\mu = N_{tot}/N_b$.
Next, we run the same random number generator, but instead of making a histogram of
$x_i$, we will take an average over some number of points ($N$), and histogram that
average. For instance, we could generate 10000 points,
calculate $X$ as the average over every 10 points, (call this $X_{10}$) and histogram $X_{10}$.
In the above, if you change the slider called "# to sum:" to anything beyond 1, you will see
what happens when you change from histograming $x_i$ to histogramming $X_N$, with $N\gt 1$.
As you can see, the distribution over the averages becomes highly peaked, more and more
as you increase the number of points in the average, $N$.
This is straight
forward to understand: when you calculate the average over say 10 points, then much of
the time you will get something near the true average, which will be at 0.5 if $0\le x_i\lt 1$
But not always. Consider how you would get an average that is far away from 0.5, say at
0.1. In that case, you will need to get pretty lucky to generate 10 random values that
are all clustered around 0.1. There are not many ways to do this, as opposed to the many
ways you could generate numbers that have an average near 0.5. So the probability of
getting something far from the true average falls fast as you go away from that average.
And so combinatorics plays a big role here: there are many more ways to generate 10 points
that form an average near 0.5 than there are ways to generate 10 points to form an average
near 0.1.
This effect is the main subject of what is known as the "Central Limit Theorem" (CLT).
There are two amazing things about CLT:
So we see here that the gaussian distribution is not merely something derived by taking
the limits for binomial distributions, but is in fact much more basic and fundamental,
and is all tied up with the notion of randomness. This is what makes the gaussian
so important: if you are doing an experiment and want to see if what you are measuring
is according to some known process, or something new, you want to understand the
random fluctuations
in the known process and compare to the experimental observations. Those fluctuations
will be (under most circumstances) described by gaussian (random) fluctuations.
If the comparison is good, then what are measuring is just a fluctuation. The question
is, what does "good" mean?
The more you get to work with and know statistics, the more you will use the gaussian
distribution. And you will get a feeling for how the gaussian quantifies fluctuations
in measurements. For instance, if you have a quantity $x$ with a mean $\bar x$, and
RMS $\sigma_x$, then the gaussian describes the probability of any particular measurement yielding the value
$x_i$:
$$ P(x_i) = \frac{1}{\sqrt{2\pi\sigma_x}}e^{-(x_i-\bar{x})^2/2\sigma_x^2}\nonumber$$
The implicit assumption here is that the true value of $x$ will be $\bar x$, so that
when you make a measurement, what you want to know is the probability that the
measured value $x_i$ will be within some finite distance from the mean $\bar x$.
That means you have to integrate the probability distribution from $\bar x-x_i$ to
$\bar x+x_i$.
In the plot below, you can see the gaussian function plotted with $\bar x=0$ and
$\sigma_x=1$. So the horizontal goes from $-10\sigma$ to $+10\sigma$. If you click
on any 2 points, the program will calculate the integral outside those points,
and display in a label above the graph. For instance, if you click on $x=-4$ and
$x=+4$, the program will calculate the probability of getting any value of $x_i$
that is $\lt -4$ or $\gt +4$.
When we make measurements, we almost always want to and compare to theory. Our theory
could be based on some real effect, or it could be that we just want to compare
to the null result. This chapter introduces
techniques of comparison, and the idea of "significance".
To start, imagine you take some data and want to compare to a theory.
For instance, you might make a series of experiments ($N$ measurements, each
one denoted by the subscript $i$) and for each measurement "i" you set an
acceleration $a_i$ on some object of unknown mass, and
measure the force $F_i$ with some uncertainty (aka "error bar") $\delta F_i$.
Each data point should obey Newton's law, to within the uncertainties from
fluctuations:
$$F_i=ma_i\nonumber$$
How can we extract the mass from all this data? One possibility is to
take the ratio of each measurement of $F_i$ and $a_i$,
and extract the average mass $\bar{m}$ by averaging over all ratios:
$$\bar{m} = \frac{1}{N}\sum_{i=1}^N F_i/a_i\label{embar}$$
This is a mathematically well defined thing to do, however
it suffers from one big drawback: we are assuming that the relationship
between $F_i$ and $a_i$ is linear, described by a line with a zero y-intercept.
It is also susceptible to ratio's where the acceleration fluctuates low,
approaching a "divide by zero" problem and skewing the average ratio.
Another possibility is to average over all $F_i$, and over all $a_i$, and take the
ratio of the averages:
$$\bar{m} = \frac{\sum_{i=1}^N F_i}{N}/\frac{\sum_{i=1}^N a_i}{N}=
\frac{\sum_{i=1}^N F_i}{\sum_{i=1}^N a_i}\nonumber$$
This is a bit better behaved (and we will see has some validity), but still
suffers from the fact that we are assuming here that there is no y-intercept in
the linear relationship between $F_i$ and $a_i$.
At this point, let's think through what we are trying to accomplish, and see if
we can come up with a better method. To start, the plot below shows the set of
data for $F_i$ and $a_i$ measurements. The $a_i$ are assumed to be "dialed up",
so they have a negligible uncertainty, and the $F_i$ are the measured forces,
each with an uncertainty $\delta F_i$. Each time you hit the "Reset" button,
it will generate an entirely new set of data, randomly:
The task at hand is to determine the "best" straight line that describes
a linear relationship between $F$ and $a$.
Your intuition here is useful: if you were to lay a pencil down on top of the
distribution of $F$ vs $a$, and eyeball the line that would best fit the data,
you would probably try for the line that goes through the most points. And
you would be pretty close. But to get the very best fit, what you would want
to do is draw a line that minimizes the distances between the y-value of the line
($y=mx_i + b$),
and the y-value of the data point ($y_i$). So if you pick a slope $m$ and intercept $b$,
then you would perhaps form the following quantity:
$$d_i = y_i - y = y_i - (mx_i + b)\nonumber$$
Summing over all points (all $N$ $d_i$'s) would give a measure of how well the theory
(the straight line) fits the data, so you might form the sum:
$$D = \sum_{i=1}^N d_i = \sum_{i=1}^N [y_i - (mx_i+b)]\nonumber$$
If you then varied the slope slope and y-intercept, and recalculated $D$ for each
new choice of $m$ and $b$, you could find the $m$ and $b$ that minimize $D$.
The problem with this particular choice of measuring how well the theory and data
match (using $d_i$) is that in the sum, some of the time the line will be below the
point ($d_i\gt 0$), and some of the time above ($d_i\lt 0$). So you could have the
situation where the individual $d_i$'s are large, but by (bad) luck
cancel each other out, giving a small value for $D$. We need another measure!
An alternative would be to just take the absolute value of the
various $d_i$ values. However it turns out that the technique that has the most
statistical validity uses the square of the
$\delta_i$'s, something intrinsically positive:
$$\sum_{i=1}^N d_i^2 = \sum_{i=1}^N \Big(y_i - (mx_i+b)\Big)^2\nonumber$$
This is close to being the best thing to do, however how will you judge whether
the value of the sum is "good" enough? And this particular technique, using
$d_i^2$, does not take into account the uncertainty $\delta_i$
in the measurement of each $y_i$.
A sensible (and as it turns out, statistically valid) way to solve both problems
is to first divide $d_i$ by the uncertainty $\delta_i$, and then square forming
the "residual" $r_i$:
$$r_i\equiv \frac{d_i}{\delta_i}\nonumber$$
By doing that, $r_i$ is measuring the vertical
distance between the measured $y_i$ point at a given $x_i$, and the $y(x_i)$
value calculated
from that $x_i$ and the line parameters $m$ and $b$, in units of the
uncertainty in $y_i$: $r_i=d_i/\delta_i$ tells you "how many uncertainties"
separate $y_i$ from $y(x_i)$. Then we form the sum over all $r_i^2$
(squared, to avoid the cancellation problem above), and call this value $\chi^2$:
$$\chi^2 = \sum_{i=1}^N r_i^2 =
\sum_{i=1}^N \Big(\frac{d_i}{\delta_i}\Big)^2 =
\sum_{i=1}^N \Big(\frac{y_i - (mx_i+b)}{\delta_i}\Big)^2\label{echi2}$$
The procedure would then be to vary $m$ and $b$ independently, forming a
new $\chi^2$ each time, and choose our final values for $m$ and $b$ that
gives the smallest possible $\chi^2$. This is what the "Solver" does for
you in Excel. Notice that in the above plot of "Force vs Acceleration",
the $\chi^2$ is given (once you input a non-zero slope and y-intercept).
The assumption made in the code is that all
of the $\delta_i$'s are the same (just to make things simple),
and equal to around $2$, just as a guess.
But in reality, you have to come up with a reasonable value for the
$\delta_i$'s, and this is one of the most important parts of doing experiments:
knowing your uncertainties. (Note: scientists often say "know your errors",
a cute expression that is actually the same thing as "know your uncertainties".)
In the plot above, you can type in a non-zero value for the slope and y-intercept,
the line will be displayed, and the code
will tell you the $\chi^2$ and number of degrees of freedom. You can change the
slope and y-intercept and see where the $\chi^2$ is minimized for the best fit.
For a linear fit, you can actually find the best slope analytically.
To keep it simple and illustrate the concept, let's choose a constant value for
all of the $\delta_i$'s (call it $\delta$). There are 2 parameters here, $m$
and $b$, so to calculate values of $m$ and $b$ that minimize the $\chi^2$,
we set the 1st derivative $\partial\chi^2/dm$ and $\partial\chi^2/db$ to 0,
and solve for the best value of $m$ and $b$. The calculation goes like this:
These formula for $m$ and $b$ are interesting, and deserve a closer look to see if we can
understand them better. For instance, let's first define a quantity that calculates the
2nd moment like this:
$$M2(x,y) \equiv \overline{x}\cdot\overline{y} - \overline{xy}\nonumber$$
Then we can show that $M2(x,x)=\sigma_x^2$, and we can rewrite the above formula for $m$:
$$m = \frac{ \overline{xy}-\overline{x}\cdot\overline{y}}{\sigma_x^2}=\frac{M2(x,y)}{M2(x,x)}\nonumber$$
This tells you something about the slope, that it is related to the ratio of the 2nd moments of
$xy$ to $xx$. But the slope doesn't tell the whole story.
For the y-intercept $b$, we first add and subtract $\overline{x}^2\cdot\overline{y}$ from the numerator
and collect terms, and after some algebra, we get
$$b = \overline{y}-m\overline{x}\nonumber$$
or in other words, $\overline{y} = m\overline{x} + b$, which tells you that the best fit is such
that the average $x$ and average $y$ fit the straight line!
The above formulae are very useful if you have an array of $x$ and $y$ values and want
to calculate the best fit for the slope and y-intercept hypothesis: just loop over all
values, calculate the averages $\overline{xy}$ etc, and out pops the result without
having to do double loops:
Once you have a value for the parameters that minimize the $\chi^2$,
you still need to ask whether that minimum $\chi^2$ is describing a "good" fit,
or not. Note that you have taken the sum of $(d_i/\delta_i)^2$.
If the fit is "good", and your uncertainties are accurate,
then you would expect that the fit curve will go
through most of the points within $\pm\delta_i$, more or less, so that
each of the $r_i$ will be "close" to 1, on average. Of course sometimes you
will have points where the fit is more than 1 $\delta$ away, and sometimes you
will have points that are less than 1 $\delta$ away, but on average, a "good fit"
should give you a $\chi^2$ where each of the $r_i$ are of order 1. So we can
expect a good fit to have the sum $\sum_{i=1}^N$ will be close to $N$.
Actually, you have to take care here, because if
you are fitting for 2 parameters (as in a straight line, $m$ and $b$), then you need at
least 2 points. If you have only 2 points, then you have no
freedom to move the slope $m$ and y-intercept $b$ around (2 points determine
a straight line), and so the $\chi^2$ for 2 points ($N=2$) will be identically
0.0. So the number of "degrees of freedom" will be, for a straight
line fit, 2 less than the total number of points, and for a good fit you
would expect that the $\chi^2$ will add up to something very close
to $N_{dof}=N-2$. And so you can look at the quantity $\chi^2/N_{dof}$,
and that should be close to 1. If it is, then it's a good fit. If it's not,
then it's not a good fit! If that ratio is much larger than 1, it means
that either the points do not describe the fit function, or it could mean
that your uncertainties $\delta_i$ are too small and in fact you have bigger
uncertainties than you thought. If on the other hand
the ratio is close to 0, it could mean that your uncertainties are too
large (or that your points are too good, which should make any scientist nervous!).
Sometimes we make measurements on more than 1 quantity at a time, and combine
them to form something that is a function of the measured quantities. For
instance, we measure the width $W$ and length $L$ of a parking lot, with
corresponding uncertainties $\delta W$ and $\delta L$. Then we want to
combine them to form the perimeter $P=2(W+L)$. To keep it simple, let's
define $P_h=W+L$, and so $P=2P_h$. Knowing the uncertainties
in $W$ ($\delta W$) and $L$ ($\delta L$, we want to know the uncertainty in $P_h$,
and deal with the uncertainty in $P$ later.
One sensible thing to do is to say that the extreme values of $W$ are
given by $W_+=W+\delta W$, and $W_-=W-\delta W$. And similarly for
$L_+$ and $L_-$. Then the extreme values of $P_h$ would be given by:
$$P_{h+}=P_h+\delta P_h = W_++L_+ = W+\delta W + L + \delta L = W+L+(\delta W+\delta L)\nonumber$$
and
$$P_{h-}=P_h-\delta P_h = W_-+L_- = W-\delta W + L - \delta L = W+L - (\delta W+\delta L)\nonumber$$
This suggests we use $\delta P_h=\delta W + \delta L$.
However, there is more to the story, going back to what $\delta W$ and $\delta L$ mean.
These quantities are usually given as the "$1\sigma$" uncertainties of the quantities
$W$ and $L$, meaning that the measured values of $W$ and $L$ will fluctuate within the
uncertainties such that $68\%$ of the time, $W$ and $L$ will be between $W\pm\delta W$
and $L\pm\delta L$. (See the above discussion on gaussian intervals.)
To be consistent, we would want to have a $\delta P_h$ that also describes the $1\sigma$
in $P_h$, however $\delta P_h=\delta W + \delta L$ clearly does not accomplish that.
The following shows this explicitly. We generate random numbers that are normally
distributed around $8$ for the width $W$, and around $16$ for the length $L$, and we use
$\sigma=1$ for both distributions. We calculate $P_h=L+W$ and plot this as well. The
mean and standard deviation are calculated from the histogram and reported in the table
above it. The fact that the standard deviations are not exactly at $1$ for the $W$ and $L$
histograms reflect the statistical fluctuations in making measurements based on the
bin contents of the histogramming.
As you can clearly see, the standard deviation of $P=W+L$ does not equal the sum of
the standard deviations of $W$ and $L$: $\sigma_{W+L} \ne \sigma_W+\sigma_L$. But this
should be expected: it is not very probable that when $L$ fluctuates by the maximum, that
$W$ will do the same, because $W$ and $L$ are uncorrelated. That is, the fluctuation
in the measurement
of $L$ does not have any effect on the fluctuation of the measurement of $W$, and so the
two fluctuations are uncorrelated and independent. This is the key reason why simply adding
the uncertainties does not work, and so we need a
better way to form uncertainties (so called "errors").
To develop a way to add uncertainties, we can define the problem in the following
way:
To keep it simple, let's start with a function that is linear, like $z=x+y$.
Going back to the quation for the variance ($\ref{evar2}$), we have the following 3
equations:
$$\sigma_x^2 = \sum_{i=1}^n P(x_i)\delta x_i^2\nonumber$$
$$\sigma_y^2 = \sum_{i=1}^n P(y_i)\delta y_i^2\nonumber$$
$$\sigma_z^2 = \sum_{i=1}^n P(z_i)\delta z_i^2\nonumber$$
where $\delta x_i=x_i-\bar{x}$, $\delta y_i=y_i-\bar{y}$, and $\delta z_i=z_i-\bar{z}$.
We can easily calculate $\bar x$ and $\bar y$, and then it's not difficult to see that
$\bar z = \bar x + \bar y$. Since we know that $z=x+y$, then $\delta z = \delta x +
\delta y$, and we have the equation:
$$\sigma_z^2 = \sum_{i,j=1}^n P(z_{ij})(\delta x_i + \delta y_j)^2\nonumber$$
Note that the sum over $ij$ means we are summing over the two distributions, $x_i$
and $x_j$, hence the peculiar notation. Let's drop this notation and just sum,
keeping in mind that there is a dual sum here.
The quantity $P(z_{ij})$ is related to the probability of seeing any particular value
of $z_i$, which involves the probability of seeing any particular value of $x_i$ and
$y_i$. In the world of probability, probabilities multiply. For instance, if you
have a particular $x,y$ pair that has probabilities of $\half$ each, then the
probability of both will be given by $P_xP_y=1/4$. So we can write
$$P(z_{ij})=P(x_i)\cdot P(y_j)\nonumber$$
The above equation for $\sigma_z^2$ becomes
$$\sigma_z^2 = \sum P(x_i)P(y_j)(\delta x_i + \delta y_j)^2\nonumber$$
Expanding the square gives:
$$\sigma_z^2 = \sum P(x_i)P(y_j)(\delta x_i^2 +
2\delta y_j\delta x_i + \delta y_j^2)\label{esum3}$$
There are 3 quantities here. The first is
$$\sum P(x_i)P(y_j)\delta x_i^2\nonumber$$
which can be written as
$$\sum P(x_i)\delta x_i^2\sum P(y_j)=\sum P(x_i)\delta x_i^2=\sigma_x^2\nonumber$$
Here we made explicit use of the fact that $\sum_{j=1}^n P(y_j)=1$ by definition.
Similarly, the 3rd equation in our troika equation $\ref{esum3}$ above is:
$$\sum P(y_j)\delta y_j^2\sum P(x_i)=\sum P(y_j)\delta y_j^2=\sigma_y^2\nonumber$$
The middle equation is actually pretty easy to understand:
$$2\sum P(x_i)P(y_j)\delta y_j\delta x_i\
=2\sum P(x_i)\delta x_i\sum P(y_j)\delta y_j=0\nonumber$$
Each term in the sum is zero by definition of the mean $\bar x$ and $\bar y$.
So, equation $\ref{esum3}$ becomes:
$$\sigma_z^2 = \sigma_x^2 + \sigma_y^2\label{equad}$$
If we look at the above histograms of $W$, $L$, and $P=W+L$, we can see that indeed
$\sigma_P^2 = \sigma_W^2 + \sigma_L^2$, and now we know that uncertainties for
sums of variables add in quandrature. And what makes this happen is that
the middle term of equation $\ref{esum3}$ is equal to 0, which comes from the
fact that the individual $x_i$ and $y_j$ are all independent of each other, or
in other words uncorrelated. So we should amend our rule and say that
uncertainties in sums of uncorrelated variables add in quadrature.
We can now try to generalize equation $\ref{equad}$ to arbitrary functions
$f(x,y)$. The equation to start with is
$$\sigma_z^2 = \sum P(z)\delta f^2\nonumber$$
where $\delta f^2 = (f-\bar{f})^2$.
We can expand $f$ around the mean $\bar{f}$ using the Taylor expansion:
$$f(x,y) = f(\bar x,\bar y) + \frac{\partial f}{\partial x}\delta x +
\frac{\partial f}{\partial y}\delta y + ...\nonumber$$
where we have stopped after 1st order in $\delta x$ and $\delta y$, and we
keep in mind that $\partial f/\partial x$ is evaluated at $x=\bar{x}$ and
the same for $\partial f/\partial y$.
Note that $\bar f$ really is $f(\bar x,\bar y)$ to first order.
This means we can then write
$$\delta f^2 = (f-\bar f)^2 = \big(\frac{\partial f}{\partial x}\delta x +
\frac{\partial f}{\partial y}\delta y\big)^2\nonumber$$
When we expand this squared quantity, we get:
$$\sigma_f^2 = \sum P(x)P(y)\big[ \big(\frac{\partial f}{\partial x}\delta x\big)^2
+ \big(\frac{\partial f}{\partial y}\delta y\big)^2 +
\big(\frac{\partial f}{\partial x}\delta x\frac{\partial f}{\partial y}\delta y\big)
\big]\nonumber$$
As we noted above, the quantities that are linear in $\delta_x\delta_y$ will vanish
if $x$ and $y$ are uncorrelated. Expanding what's left (the first 2 parts of the
above equations) and summing $\sum P(y)=\sum P(x)=1$, we are left with:
$$\sigma_f^2 = \sum P(x)\big(\frac{\partial f}{\partial x}\delta x\big)^2 +
\sum P(y)\big(\frac{\partial f}{\partial y}\delta y\big)^2\nonumber$$
One last thing to do: the quantity $\partial f/\partial x$ (and $y$) is
evaluated at $\bar x$ (and $\bar y$), which means they are not a function of $x_i$ or $y_i$,
which means you can bring them out of the sum. What's left is just
$\sum P(x)\delta_x^2=\sigma_x^2$ (and same for $y$), which gives us:
$$\sigma_f^2 = \big(\frac{\partial f}{\partial x}\delta x\big)^2 +
\big(\frac{\partial f}{\partial y}\delta y\big)^2\label{eerrprop}$$
and again, the main thing here to remember is that this is correct if
$x$ and $y$ are uncorrelated, and of course is only good to 1st
order in the uncertainties. That means that if the uncertainties are
of order $10\%$ of the values, then the correction to this equation
would be of order $(10\%)^2 = 1\%$.
As an example, say that $f(x,y)=x/y$. Then
$\partial f/\partial x = 1/y$ and $\partial f/\partial y=-x/y^2$,
which gives us the relation
$$\sigma_f^2 = \delta x^2/y^2 + x^2\delta y^2/y^4\nonumber$$
If we form $\sigma_f/f$, we get
$$\frac{\sigma_f^2}{f^2} = \frac{\delta x^2}{x^2} + \frac{\delta y^2}{y^2}\nonumber$$
What we want to do in physics (and any other science) is to try to
understand nature by coming up with theories, doing experiments,
and seeing if the theories and experimental results agree.
For instance, if we apply a force $F$ on a mass $m$ and measure
the acceleration $a$, we could use the ratio $F/a$ and compare to the
mass $m$. If they agree, then our theory $F=ma$ is valid. If they don't agree,
it's back to the drawing board.
But the world is complicated, because any measurement
will come with a corresponding uncertainty, and any particular value
measured will come from some true value that has fluctuated. So even
if our theory is correct, we will often find that $F/a$ is not equal
to $m$ for any particular measurement!
To be concrete,
when we make a measurement, say $M_i$, we are thinking that there exists
a true value, $T$, and that the difference between the two comes from
fluctuations:
$$M_i = T + \delta_i\label{xfluctuation}$$
We measure $M_i$, and we have an understanding of the uncertainty $\sigma$,
but we don't know $T$ (we are trying to find it!) and so we don't know
the size of the fluctuation $\delta_i$ that caused the true value to come out
as $M_i$. Note that $\sigma$ is not the same as $\delta_i$:
$\sigma$ is an educated guess about the average fluctuation, and
how precise is our measurement $M$, whereas $\delta_i$
is the actual fluctuation from $T$ for measurement $i$.
Back to our example of trying to see if $F=ma$ holds, we can make a
series of measurements where we place a force $F_i$ on a mass $m$,
and measure the acceleration $a_i$.
Even if each individual measurement fluctuates, it is probably the case
that sometimes the fluctuations will be high, and sometimes low, but that
on average the true physics will come out.
So after some number of measurements, your data might look like the following plot.
The standard theory from Newton's laws of gravity
tells us that $a=F/m$, so that a plot of $a_i$ vs $F_i$
should show a straight line with slope $1/m$.
However, experimental uncertainty
means that each measurement will fluctuate, so even though any given data point
might deviate from the true linear relationship
with slope $1/m$, the data should show a linear
trend on average.
The plot above does look like there's a linear relationship, but you can imagine
that there are many different
slopes that can go through all the values, each with a different $\chi^2$
(see above).
What we want to do is find the
slope that minimizes the $\chi^2$, and compare that $\chi^2_m$ per DOF to 1
to get an idea of whether the theory
is consistent with the data - the further away from 1, the worse the fit.
So ultimately, to quantify the extent to which this minimum $\chi^2_m$ is
consistent with our theory given our uncertainties, we need to come up with
a probability that a fluctuation could give us this particular $\chi^2_m$,
or larger. If that probability is small, then it means
it's not so likely a fluctuation, which could indicate that the theory is not
a good fit to the data. Of course "too small" is subjective, and a subject
of great almost religious debate. This probability (that the data fit the
theory) is called the $p$-value. What we want to do in this chapter is to
figure out how to calculate the $p$-value, and related concepts (the "confidence
level", and "significance").
Note that it is up to the experimenter,
and the community of scientists, to agree on a cutoff
value for $p$ to indicate agreement with the theory.
In the world of biology, a $p$-value less than $0.05$ (5\%) is often
the metric for whether the experiment is "significant" or not. But
be careful here, because a $p$-value of $0.05$ means that if you do
the experiment 20 times, then you should see this kind of fluctuation
once, on average! That doesn't mean $0.05$ is not a good cutoff.
Since a small $p$-value means that the $\chi^2_m$ (per DOF) is
somewhat large, a $p$-value of $0.05$ is an indication that either
your theory is looking like it might be
incorrect (large numerator in the $\chi^2$) or your
uncertainties are too small (small demoninator), and this could serve
as a good guide for checking things as you go along.
To investigate how we can calculate a $p$-value, we
go back to the discussion of the $\chi^2$ and $N_{dof}$, and
consider an experiment with 2 measurements $x_1$ and $x_2$, with
uncertainties $\sigma_1$ and $\sigma_2$.
If we form the mean $\bar x=\half (x_1+x_2)$, we can then
form the $\chi^2$ with two terms:
$$\chi^2 = \frac{(x_1-\bar x)^2}{\sigma_1^2} +
\frac{(x_2-\bar x)^2}{\sigma_2^2}\nonumber$$
The quantities $x_1$ and $x_2$ are both distributed normally about the mean
with widths
$\sigma_1$ and $\sigma_2$, and since we've already used $x_1$ and $x_2$ to
form $\bar x$, our $\chi^2$ has 1 degree of freedom, which we can see
explicitly by substituting for $x_2 = 2\bar{x}-x_1$ to get
$$\chi^2 = \frac{(x_1-\bar{x})^2}{\sigma_1^2}\big(1-\frac{\sigma_1^2}{\sigma_2^2}\big)\nonumber$$
If we define $y \equiv (x_1-\bar{x})/\sigma_1$, then $y_1$ will be
distributed normally about $y_1=0$ with width $1$, and we can write the
probability distribution of $y$ as:
$$P(y_1) = \frac{1}{\sqrt{2\pi}}e^{-y_1^2/2}\label{pofy}$$
and we can write the $\chi^2$ as:
$$\chi^2 = y_1^2\times k\nonumber$$
where $k = 1-(\sigma_1/\sigma_2)^2, which is just a number$.
So if we know $P(y)$, then we should be
able to calculate $P(y^2)$ and that will give us $P(\chi^2)$ for 1 DOF.
There are many ways to do the math here, so let's try the simplest:
since $P(y)$ is a probability, and since probabilities all have to integrate
to 1, we can write:
$$\int_{-\infty}^{+\infty} P(y)dy = 1\nonumber$$
where $P(y)$ is given by equation $\ref{pofy}$ above. If we substitute
$z\equiv y^2$, use $dz = 2ydy$, and note that the integral is symmetric over the
range between $-\infty$ and $+\infty$, we have
$$2\int_{0}^{+\infty} \frac{1}{\sqrt{2\pi}}e^{-z/2}\frac{dz}{2\sqrt{z}} = 1\nonumber$$
which means we can read off the probability:
$$P(z) = \frac{1}{\sqrt{2\pi z}}e^{-z/2}\nonumber$$
This derivation works well for our simple case with 2 measurements $x_1$ and $x_2$,
where we have 1 degree of
freedom, but for more
degrees of freedom, the complications due to the nature of probability set in, and
the $\chi^2$ per degree of freedom probability distribution gets much more complex.
Now we can calculate the $p$-value easily: just integrate $P(\chi^2)$ from your
$\chi^2_m$ to infinity to get the probability that our $\chi^2$ came out at
$\chi^2_m$ or larger.
For completeness, here is how you calculate the $p$-value for various degrees of
freedom ($p(N)$ where $N$ = DOF):
$$p(\chi^2_m,1) = \int_{\chi^2_m}^\infty \frac{1}{\sqrt{2\pi z}}e^{-z/2}dz\label{p1}$$
$$p(\chi^2_m,N) = \int_{\chi^2_m}^\infty \frac{z^{(N/2-1)}e^{-z/2}}{2^{(N/2)}\Gamma(N/2)}\label{pN}$$
where $\Gamma(N)=(N-1)!$ for integers, and for non-positive integers is defined as:
$$\Gamma(x) = \int_0^\infty y^{x-1}e^{-y}dy\nonumber$$
Below we see the distribution of $p$-value vs
$\chi^2_m$ for the situation where you have 1 degree of freedom (see equation
$\ref{p1}$ above).
In Excel, you can use the CHIDIST function to give you the $p$-value. You
give it the $\chi^2_m$
and $N_{dof}$, and it integrates the probability between your value and
infinity.
For the case where there are 3 data points and 1 parameter, the number
of degrees of freedom is 2, and the 3 data points are all allowed to fluctuate
independent of each other.
If each data point fluctuated $\sqrt{2}$ relative to the uncertainty
$\delta_i$, then each term would contribute 2, and the $\chi^2_m$ would
be at around 6.
In fact, the $\chi^2$ that gives a $p$-value of $p=0.05$ for 2 degrees of
freedom is 5.99, and the reduced $\chi^2$ ($\chi^2/N_{dof}$) is around $3.0$
If we go to 4 data points, or 3 degrees of freedom, then we would expect
$p=0.05$ would give a $\chi^2$ of around $8$, and in fact the real value is $7.81$
with a reduced $\chi^2$ of $2.6$.
That the $\chi^2$ for $p=0.05$ is less than $8$ is because for so many points,
you could have the situation where one fluctuations low and another high, and
the low fluctuation pulls the $\chi^2$ down a bit.
So as we go to a larger and larger number of degrees of freedom, we might expect
that the reduced $\chi^2$ approaches $1$.
This is exactly what we see in the following plot of the reduced $\chi^2$ vs the
number of degrees of freedom that gives $p=0.05$ - it does tend towards $1.0$ as
$N_{dof}$ increases to $100$ and beyond.
Combinatorics
Imagine doing an experiment where
you ask some number of strangers for their birthday, and make a histogram
of what how many people had birthdays on any particular day
(where day means day and month as a sequential number from 1 to 365).
The histogram will have 365 bins,
and the sum of all the entries in the bins adds up to the total number
of people you queried ($N$).
One would expect that all days should have the same probability $p=1/365$ of
being a birthday. Of course, there could be biases that favor some days over others,
for instance one could imagine that maybe more people were
conceived on holidays than non-holidays, therefore the birth dates should
cluster around holidays plus 9 months. But let's assume the probability $p(n)$ of any
random birthday to be on day $n$ is given by $p(n)=p=1/365$.
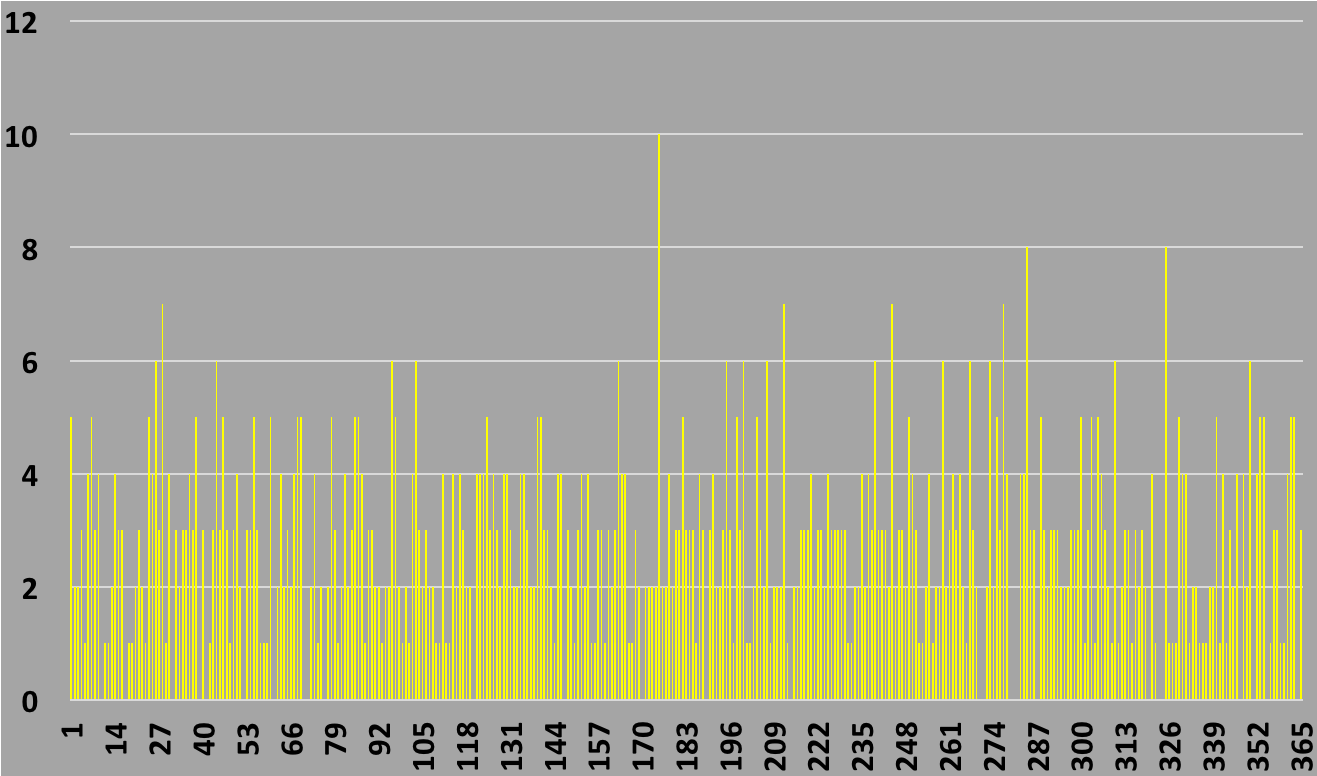
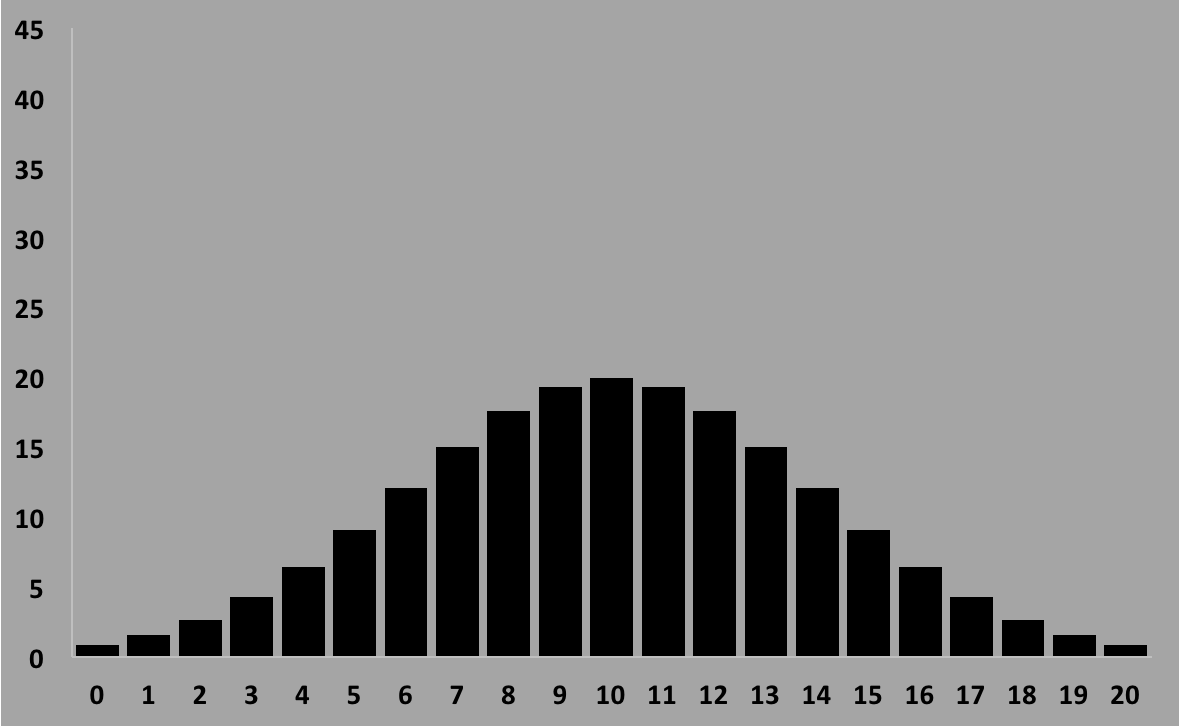
Figure 1. Histogram of birthdays of $N=1000$ sample.
So we can see how the binomial distribution can be used to solve problems that
involved probabilities and combinatorics.
Now we can calculate the probability (call this $M(5,2)$) that in a room of $N=5$
people, at least 2 of them have the same birthday as Mozart. Since "at least 2"
means 2, 3, 4, or 5, then we add those probabilities together:
$M(5,2)= P(2)+P(3)+P(4)+P(5)$. Or, since
the sum of all probabilities is 1, we can instead use $M(5,2)= 1 - P(0) - P(1)$.
Since $P(0)=98.63\%$ and
$P(1)=1.35\%$, then $M(5,2)=1-99.993\%=0.0075\%$.
The Birthday Problem
To finish this example, let's say you have a room of $N$ people, you
make a histogram of birthdays, normalize it so that it's a probability distribution,
and ask for the probability that at least 2 people have the same birthday. Or better
yet, you ask for the number of people (what is $N$)
such that the probability that any 2 have the
same birthday be at least 50%.
Combinatorics and Throwing Dice
Unfortunately there are characters in the world who cheat, and to cheat in dice all
you have to do is "load" the dice so that you get the right face showing more often
than not. Imagine that your cousin who owns a gambling establishment offers to pay
you to test some dice to see if they are loaded, you will need to know what you are
doing!
So now let's attack the problem of calculating the expected probability distribution
for situations with combinatorics using the dice.
Then we will do the experiment, roll the die $N$ times, and measure the frequency
$f(n)$ for seeing face $n$ appear, and compare it to $\bar{f}(n)\pm\delta(n)$.
This will give us an idea of whether the die is loaded or not.
All you have to do now is roll the die $N$ times, make a histogram of how many times
you see face $n$ apear, and compare that to what the binomial distribution predicts,
which is that each face will have an equal mean and variance after $N$ rolls. If you
find one of the faces that is very different from any of the others, then that die
is loaded. Of course, we have to define what we mean by "very different", and this
turns out to be where science meets art (more below)!
Poisson Distribution
The binomial distribution is a general case, and somewhat complex. Sometimes, however,
the situation you are in will have a small probability $p\lt\lt 1$, a large number $N$,
and you want to know the probability $P(n,N)$ where $n\lt\lt N$.
For instance, imagine we were to ask $N$ people for their birthday, and tablulate
the date as the ith day of the year (from 1 to 365). Then we would want to calculate
the expected frequency probability distribution for any particular day to have 2, 3,
4, 5, etc birthdays. For example, you ask 365 people for their birthday, and want to
know the probability of there being 2 birthdays in any given day. Or 3 birthdays. And
so forth. This will again involve the binomial distribution, because you are dealing
with the combinatorics (the combinatorics and associated probabilities for taking $N$
things $n$ ways).
But here, the probability of any given day will be quite small, and if all days are
equal, we should have $p=1/365$. If we took the data ($N$), made the histogram of how
many days had 2, 3, etc ($n$) people, and compared to what you would expect, you could
maybe see if there was some reason why some days would be more preferred or not (for
insance, perhaps more birthdays 9 months from holidays).
Here, the number of possibilities in the stream is 365 ($p=1/365$), which is quite a
small number. If you took $N$ samples, then the average for each day will be given
by the mean of the binomial distribution, or $\bar{n} = Np$. So if you sampled 365
people, you would expect $\bar{n}=1$, but you might actually find that some days had
2, even maybe 3. But you would not expect that some days would have anywhere
near 365!
We can investigate how the binomial distribution behaves by doing the relevant expansions,
and there are several equally complex ways to do this. One very straightforward way is
to do make the following approximations:
A brief word on the approximation made above, that $Np = \mu \lt\lt 1/p$. The probability distribution
will max out in the region where $n\sim \mu$, and will fall to zero way outside that region. So as
long as we keep away from distributions where $\mu$ is close to $N$, we are ok.
For the birthday example, this approximation will hold as long as the average
number in any day is less than $1/p=365$. This also tells us that $N\lt\lt 1/p^2\sim 10^5$,
so it sets a limit on $N$
Log scale?
$\mu =$
# pts to plot =
Gaussian Distribution
As we just saw, the poisson distribution is the binomial
distribution in the limit of $p\lt\lt 1$ and $n\lt\lt N$, but $pN=\mu$ is finite.
Both are distributions over discrete values, and usually have to do with predicting
the results from counting experiments. Using Stirling's rule, we can turn the
poisson into a distribution over continuous variables, or we can calculate it from
first principles. One can then look at poisson distributions when the mean $\mu$ is
quite large, and when $n$ is large, and after taking the limits one can get
the following distribution:
$$P(x,\mu)=\frac{e^{-(x-\mu)^2/\mu}}{\sqrt{2\pi\mu}}\nonumber$$
If we use the fact that both the mean $\bar{x}$ and the variance $\sigma^2$ are
both equal to $\mu$, we can substitute in the above formula to get:
$$P(x,\mu)=\frac{e^{-(x-\bar{x})^2/\sigma^2}}{\sqrt{2\pi\sigma^2}}\label{egaussian}$$
This is called the gaussian distribution, and is probably the most important and
ubiquitous distribution in all of science.
# to generate:
# bins in histogram:
# to sum:
Average number per bin $\bar {N}:$
$\bar{x}=$
$\sqrt{\sigma^2}=$
Central Limit Theorem
It can be shown that the distribution for the average approaches the gaussian as
the number of points in the average ($N$) approaches $N_{tot}$, with a variance given by:
$$\sigma^2_{Gaussian} = \frac{\sigma^2_{random}}{N}\nonumber$$
where $N$ is the number of random values to include in each mean that is histogrammed.
In the above, if you select "Averages", then the histogram will be of the averages
$X$, and the line will be a gaussian that uses the mean $\bar x$ and RMS $\sqrt{\sigma^2}$
as the 2 parameters. You can see that the difference is pretty small! It is
educational to play with the parameters to get a feeling for this: try increasing the
number of points to generate, and the number of points for averaging, and notice how
the variance changes: you should see it get smaller and smaller as the number of points
in the average gets larger and larger. This reflects the falling probability of seeing
combinations of $x_i$ that are all far away from $\bar{x}$.
Log scale:
between $\pm$
$\chi^2$
Back to top
Slope $m$: Y intercept $b$:
$\chi^2=$
DOF=
Linear Fit, Analytically
$\chi^2$ $=$ $\sum_{i=1}^N \Big(\frac{y_i - (mx_i+b)}{\delta_i}\Big)^2$
$=$ $(1/\delta^2)\sum (y_i - mx_i-b)^2$
//
// "x" and "y" are in arrays x[i] and y[i], and we sum from 0 to nbins-1
//
sumy = 0;
sumx = 0;
sumx2 = 0;
sumxy = 0;
for (var i = 0; i < nbins; i++) {
sumx = sumx + x[i];
sumy = sumy + y[i];
sumx2 = sumx2 + x[i]*x[i];
sumxy = sumxy + x[i]*y[i];
}
avx = sumx/nbins;
avy = sumy/nbins;
avx2 = sumx2/nbins;
avxy = sumxy/nbins;
variance2 = avx2 - avx*avx;
slope = (avxy - avx*avy)/variance2;
y_intercept = (avx2*avy - avxy*avx)/variance2;
Uncertainties and Error Propagation
Back to top
Mean $\sigma$
$W$
$L$
$P$
How do we form the uncertainty in $z$, called $\sigma_z$?
The $p$-value
Back to top
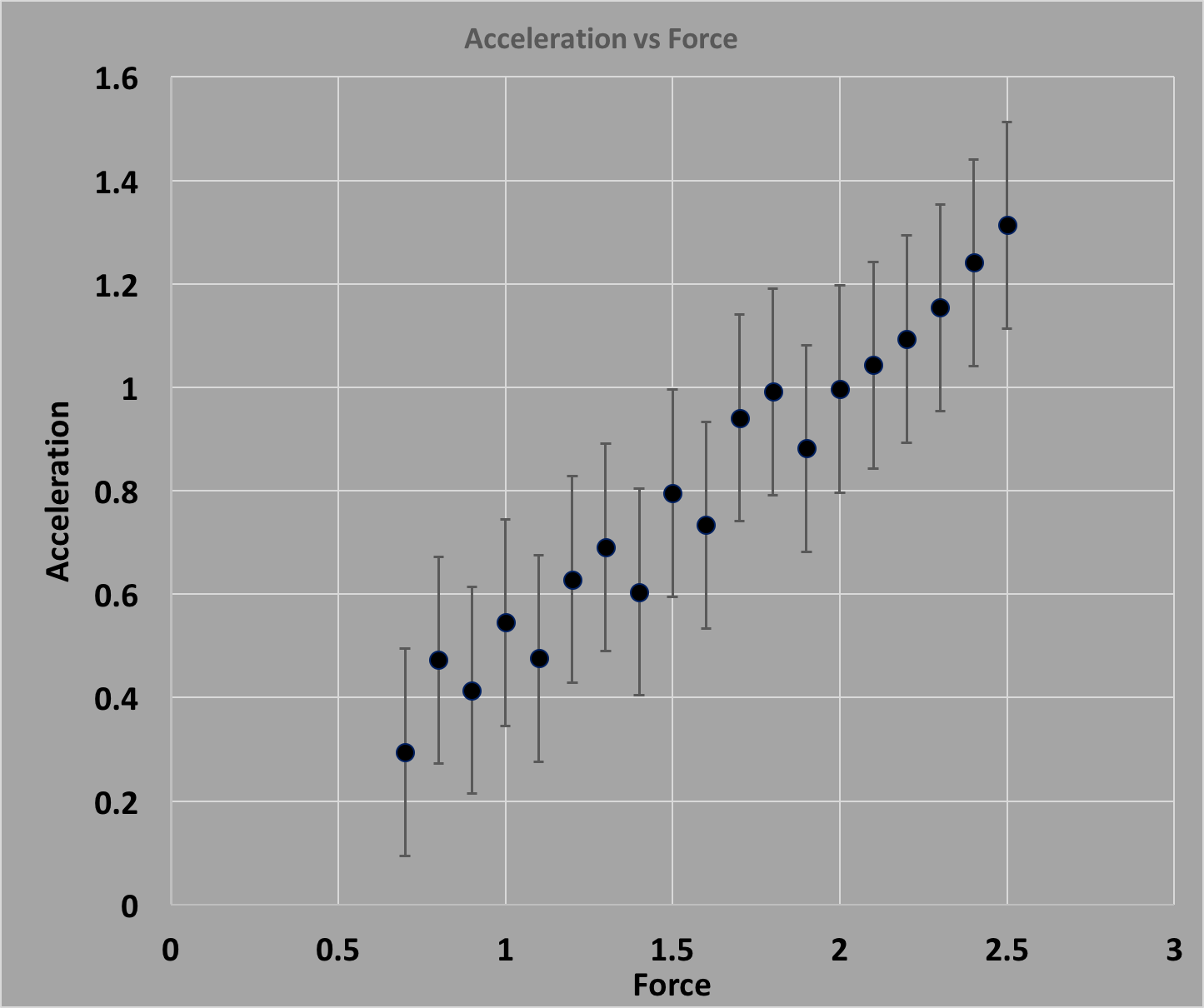


Significance and Confidence Interval
Back to top
Ultimately, what we want to do is to make a measurement, and find some way to quantify whether this measurement is "significant", that is, whether it adds up to anything, or not. And of course, this means that we have to factor into it what we expect. So we will need to define what significant means, relative to what we expect, and this leads us into the idea of confidence intervals, and the concept of "how many sigmas".
To be more specific, say we have a theory (let's call it the "standard theory") that predicts that an ensemble of experiments will yield a value $\mu$ for some quantity. Each measurement we make will yield a different $x_i$ with an uncertainty ("error") of $\delta_i$. We know how to make a $\chi^2$ that tells us how close each $x_i$ is to $\mu$ in terms of the uncertainty $\delta_i$:
$$\chi^2 = \sum_{i=1}^N \frac{(x_i-\mu)^2}{\delta_i^2}\nonumber$$
Conceptually, what we are doing here is using classical statistics and probability to quantify how well our theory ($\mu$) fits our data.
When we do such experiments comparing theory to data, if we find that the comparison is good, then this tells us that the theory holds some water. If on the other hand we find that the comparison is not so good, then this tells us 1 of 2 possible things, either:
Note that in this case where the data and the standard theory are not so consistent, you can't know in principle whether item 1. or 2. is correct! A common thing to do is to assume the standard theory is ok, use the $\chi^2$ approach to find the minimum $\chi^2_m$, and calculate the probability that we should get such a value or larger for $\chi^2_m$ for the number of degrees of freedom we have, which is how we calculate the $p$-value: $$p = P(\chi^2_m,N_{dof})\nonumber$$ If the $p$-value comes out to be $0.05$ or less, then in some cultures people say that the data and theory are consistent. If the $p$-value is greater than $0.05$, then it means the standard theory is either "probably" not correct, or it's actually ok but we got unlucky and saw a large fluctuation. Sometimes people will call the standard theory the "null hypothesis", where the use of the word "null" means "not new". So a cut of $0.05$ is used such that for $p > 0.05$, we have consistency with the null hypothesis, and below we do not. However, we have to be careful: a $p$-value of $0.05$ means that there was only a 1 in 20 chance that the data fluctuated from what the theory says it should be (or bigger), and what we found. But $0.05$ is not so unlikely: if we did 20 different experiments comparing a correct theory to data, then on average 1 out of every 20 will show a fluctuation with a $p$-value of $0.05$. Of course all you have to do is decrease the $p$-value cutoff from $0.05$ to something smaller to designate that the null hypothesis is so unlikely that we are sure we are seeing something new.