The Basic Axiom | Back to top |
The labels "x", "y", and "z" are variables. Imagine that you want to tell some small robot how to go from the corner where the dashed lines meet (the "origin", marked as "O") to any point inside the ship. To do this, you tell the little robot how far to walk along "x", how far along "y", and then how far above the floor, along "z". So all you have to do is tell the robot what those 3 numbers are, and it can find it's way to the new location. It turns out that in order to specify any arbitrary point inside the ship relative to the origin (where x=0, y=0, and z=0), you need to give it 3 numbers. Don't be confused about how if you just want to get to the end of the "y" axis you only need to tell the robot how far along "y", so it's just one number. The robot just follows the algorithm of "how much along x", then "how much along y", then "how much along z" above the floor. If you just want to go to the end of the "y" axis, then you tell it "0 along x", "how much along y", and "0 along z". So you have to give it 3 numbers: (0,y,0) to get to that specific point, or in general (x,y,z) to get to any arbitrary point inside the volume. This is what a coordinate system is, and how you would use it.
And so the ship is the framework for the coordinate system, and you use the coordinate system to reference any point inside the framework. What physicists usually do is call this a "reference frame". And in our particular case the reference frame is moving at a constant velocity somewhere far away from any effects of gravity. And this reference frame, like all reference frames, concern itself with the 3 dimensions of space. This is important - space has 3 dimensions.
Here is a puzzle to solve: Imagine you were stuck inside the ship with no way to look out or measure anything that has to do with what's outside the ship. And imagine that you were moving at some constant velocity, but the actual value of that velocity is unknown to you. Could you do an experiment, measuring some quantity, any quantity, that would allow you to know what your velocity is? And if so, what would you measure? For instance, say you have a spring inside a tube that you compress with a ball and release, propelling the ball forward (still inside the ship). If you were to measure the velocity of the ball, could you use that to measure the velocity of the ship?
This question of absolute velocity is an old one, and one that was at the forefront of theoretical physics in the 19th century. It's related to the question of "what is an electromagnetic wave" - what is actually vibrating when an EM wave propagates? Some kind of "ether" (like water, that mediates water waves)? When people tried to measure the ether, they found that they could not detect it, that there is no absolute reference frame, at least not measurable. When considering EM waves, Maxwell's equation tells us that such waves travel at a fixed velocity "c", with c=$3\times 10^8$m/sec, in any reference frame! Huh? How can that be? Surely if I shine a flashlight forward, and you are in a reference frame moving at .4c in the same direction as the light, wouldn't you see light moving away from you at .6c? Well, if you did, then Maxwell's equations should have .6c in them for your reference frame. But it does not - it has a velocity "c", regardless of reference frame. So Maxwell's equations, which are both beautiful and descriptive, was one of the first hints about whether there were any absolute reference frames (aka "ether").
Back to your space ship. You might decide that what you need to do to measure your absolute velocity is to measure the speed of light - if you measured anything other than $3\times 10^8m/s$, then that would tell you what your absolute velocity is! Because all you would have to do is turn on your rocket engines (which were off by the way, since you are moving at a constant velocity) and change your velocity, and remeasure the speed of light, and keep doing this so that the speed of light was maximized. Whatever velocity you had at that time should be the velocity of the "ether", absolute zero!
But you would find that no matter what velocity you gave the ship, the measurement of the speed of light inside the ship would always be $3\times 10^8m/s$. The logic here is simple: apparently there is no absolute spatial reference frame, and the laws of physics are such that the same things happen in the same way in any reference frame moving at a constant velocity. And that one constant velocity is as good as another! This is pretty much the basic axiom of special relativity.
Transformations | Back to top |
It should be easy to come up with such a formula: the y-coordinates are unchanged, so $y =y'$. The x-coordinates are different only by the distance $D$ in the time $t$ that the frame $O'$ has travelled, and since velocity is uniform (constant), we should have $D = vt$, so the equation for "transforming" from $O$ to $O'$ will be $$x=x'+vt\label{eq1}$$ $$y=y'\label{eq2}$$ But here's the problem: if the point at ($x',y'$) moves with some velocity $u'$ along the $x'$ direction as measured in $O'$, what would someone in $O$ measure for that velocity ($u$)?
By calculus, if you just took the derivative with respect to time in equation (\ref{eq1}) above, you would get $u = u' + v$. Can you see the problem here? If both $u'$ and $v$ were say 0.6c, then $u$ would be 1.2c! So this transformation can't be right. What to do? Where did we go wrong? A hint: we left out a 3rd equation above which was implicit, that time is measured the same in both frames: $$t=t'\label{eq3}$$ But is time the same in both frames? Here is a simple example that should make you question that!
Simultaneity and Lorentz Transformations | Back to top |
What you should be able to notice is that for the non-runner, the waves from either side reach him at the same time: simultaneously. But will the runner agree? No, he will not, he will say that he saw the flash from the bulb on the right (the one he's running towards) first, then the one from the left second. In other words, he will say that the two events (seeing the flash from each bulb) did not happen simultaneously. Now, we have to be very careful here or we can get easily confused. First we need to define the frames: let $O$ be the frame of the physicist standing still, and this happens to be the reference frame of the 2 light bulbs. When the standing physicists sees both flashes, he and the bulbs are in the same frame, so he would measure zero time difference between seeing the two flashes. That is what is meant by "simultaneous". The running physicist will be in frame $O'$, moving with some velocity (call it $v$ but we do not need to know its value) relative to $O$. The physicist in reference frame $O'$ is measuring the time between two events that are taking place in $O$, but he is doing the measurement in his frame, $O'$. When he does this, he does not get a zero time difference: he will say that the two events did not happen simultaneously in his frame. Which is correct? The answer is that the entire idea of simultaneity is evidently relative, and so absolute simultaneity does not exist. And so this is telling us that indeed, equation (\ref{eq3}) is probably what we should be thinking about! Of course, this simulation is not very realistic, because in the world we are familiar with, you can't run very fast compared to the speed of light, so as soon as the runner gets parallel to the standing physicist, the light flashes, and they will both pretty much agree on simultaneity.
So we clearly need to rethink those equations. What do you use for a guiding principle? How do we start? Given what we learned about in the simultaneity simulation, we know that any new equations we come up with for the transformation between two reference frames will have to reduce to the above equations in the limit of $v\lt\!\lt c$. So let's write down a possible solution that might be the easiest and simplest way to go:
First, define \beta =v/c, a very useful quantity. $\beta$ is between 0 and
1, the former being what we are used to, the latter being "relativistic". For light,
$\beta=1$.
Then as a guess to the form of the correct equations, the easiest thing would be to do this:
$$x=\gamma (x'+\beta ct')\label{eq4}$$
$$y=y'\label{eq5}$$
$$ct=\gamma (ct'+\beta x')\label{eq6}$$
Notice several things here:
$$dx=\gamma (dx'+\beta c\cdot dt)\label{eqd4}$$
$$dy=dy'\label{eqd5}$$
$$c\cdot dt=\gamma (c\cdot dt'+\beta dx')\label{eqd6}$$
Perhaps the first thing to do is to use these new equations, (\ref{eq4}-\ref{eq6}),
or (\ref{eqd4}-\ref{eqd6}), and see if
that gives us a better value for how velocities transform: that is, if we have something
moving with velocity $u'$ in $O'$, what would someone in $O$ measure for $u$?
Note that $u=dx\!/\!dt$ and $u'=dx'\!/\!dt'$, and what we are after is
how to calculate $u$. So, turn the crank:
$u = \frac{dx}{dt}=\frac{dx}{dt'}\cdot\frac{dt'}{dt}$
by the chain rule. We can calculate
$\frac{dx}{dt'}=\gamma(u'+\beta c)$ calculating
(remember that
$u'=\frac{dx'}{dt'}$). We can also calculate
$\frac{dt'}{dt}$ by calculating $\frac{dt}{dt'}$ using equation (\ref{eqd6})
to get $\frac{dt}{dt'}=\gamma(c+\beta u')$ and
dividing to get:
$u=\frac{dx}{dt}=\frac{\gamma(u'+\beta c)}{\gamma(c+\beta u')}=\frac{u'+\beta c}{c+\beta u'}$
Now we have to check if we get the result that the speed of light $c$ is the same
in both frames: set $u'=c$ and we can see easily that we get $u=c$ as well.
So it looks like we are right - equation (\ref{eq3}) needed to be changed, reflecting the fact
that since simultaneity is relative, then so must be time as well!
But you might ask what about $\gamma(\beta)$? Why doesn't this enter into
the equation for how velocities transform?
Maybe we don't need it, if all we have to do is modify (\ref{eq3}) into (\ref{eq6})?
The answer is that we have more work to do to understand the implications of this
principle of special relativity (that there is no such thing as an absolute spatial
reference frame, and that the laws of physics reflect this). What we have to do is
put the ideas of simultaneity being relative together with the idea that the speed of
light is the same in all reference frames, and see if we can use that to constrain
the equations (\ref{eq4})-(\ref{eq6}),
specifically to figure out $\gamma(\beta)$.
$\gamma (\beta )$ | Back to top |
Click to run the simulation and to reset it.
In frame $O'$, the light travels a total distance $\Delta y'=2H$ in a time period $\Delta t'$. Since the speed of light is constant in all reference frames, we would then have $c=\Delta y'\!/\!\Delta t'$, or $2H=c\Delta t'$ using $\Delta y'=2H$.
In frame $O$, the light travels a total distance $2L$ in a time period $\Delta t$. We can calculate the total distance $2L$ in terms of the vertical and horizontal distance using the Pythagorean theorem:
$L^2=v(\!\frac{\Delta t}{2}\!)^2+H^2$
Using the same rule that the speed of light is the same in all reference frames, we can calculate the total distance traveled in $O$ is equal to the velocity ($c$) times the time it takes ($\Delta t$), or $2L=c\Delta t$.
Now we can substitute for L and H to get
$(\!c\frac{\Delta t}{2}\!)^2=(\!v\frac{\Delta t}{2}\!)^2 + (\!c\frac{\Delta t'}{2}\!)^2$
Rearranging terms and getting rid of the factor of 1/2 gives:
$(c^2-v^2)\Delta t^2 = c^2\Delta t'^2$
Now, divide by $c^2$ and use $\beta\equiv v/c$ to get
$\Delta t'^2=(1-\beta^2)\Delta t^2$
This is a very interesting result, but how is it useful? To see that, let's do a calculation from first principles using equations (\ref{eq4})-(\ref{eq6}), and maybe we can use that to find what $\gamma(\beta)$ is.
Take equation (\ref{eq6pp}). Why? Because that equation relates time intervals in frame $O$ to both time and space intervals in the moving frame $O'$. These intervals measure the starting and ending of what we can call an "event", meaning the time and space when the laser light starts, and when it ends. This equation is very convenient because in $O'$, $\Delta x'=0$! Given that, we see right away that
$$\Delta t=\gamma \Delta t'\label{eq7}$$
Voila! We now know the last piece:
$$\gamma = \frac{1}{\sqrt{1-\beta^2}}\label{eq7p}$$
This has the right form: $\gamma\to 1$ as $\beta\to 0$.
Before moving on, it's important to understand what equation (\ref{eq7}) is telling us. In
this situation, we are measuring a pure time interval in a reference frame (here
$O'$). It's like looking at a stopwatch and measuring the time between two
events in that frame.
Equation (\ref{eq7}) tells us what someone in another frame would get if they were to
measure the time between the two events. Now be careful: the events in $O'$ are
not moving in that frame. $O'$ has a velocity relative to $O$, but
in $O'$ these events are stationary in space, so we say that $O'$ is the
proper frame and the time difference between the two events in that frame is
called the proper time and as measured in $O'$ is $\Delta t'$.
What equation (\ref{eq7}) is saying is that since simultaneity is relative, not absolute,
that when someone in frame $O$ measures the time between the events that take place
in $O'$, one will get a different answer, because 1) $O'$ is moving with
respect to $O$; and 2) the transformations tell us that space and time are
mixed up. This is the famous time dilation,
and says that the
proper time between two events is always minimal, which means that the time
measured between
events in anything other than the proper frame will be greater than the
proper time.
Is this just an artifact of mathematics? Well, note that there's a particle called the
muon ($\mu$), and it decays with a half life of around 2\mu sec
(2 millionth's of a second) as measured in a lab where the muon is at rest.
The proper time between the two events - creation and decay - is 2\mu sec
and so the theory above predicts that that time, if measured in a frame where the muon
is moving, will be larger.
It turns out that muons are also created in great numbers from the interaction of cosmic
rays with the upper atmosphere, and they will be moving rather fast as the cosmic rays
are very energetic.
Let's imagine that a muon has a velocity in the "neighborhood" of $c$.
That means it will travel
with a velocity around $3\!\times\!10^{-8}$m/s, so in its
2\mu sec lifetime it will go about 600m, less than 1 km, before decaying.
On average that is, with slower muons traveling less distance than faster ones.
The height of such cosmic ray interactions of course varies, but the upper atmosphere
can be 10s if not 100s of km high.
But we see copious numbers of muons here in labs on earth from cosmic ray interactions -
this is time dilation at work!
Space-time | Back to top |
But first, let's consider how we go from 3-dimensional vectors to 4-dimensional objects. In regular space, we are familiar with the concept of vectors. These are objects that have a starting point, a direction, and a length. They point from one spatial location to another. What's important about vectors is that they can be represented in may different ways using many different coordinate systems (for instance, an infinite number of Cartesian coordinates that differ only by the angle between the various x-axes) but they still have as their "invariant" that they point along some direction, and have a definite length. So it doesn't matter how you represent the vector - the representation won't change the length, and that it points from one point to another. In the space below you can see for yourself - rotate the axes, and see the coordinates change accordingly. But the vector itself, it stays the same.
Angle:
0
The "invariant" here is the length $\Delta r$ (the direction changes relative to the coordinate axes choice). Using the Pythagorean theorem, we know the invariant length: $$\Delta r^2=\Delta x^2+\Delta y^2\label{eq8}$$ Now, how do we extend this idea into space-time? We need to come up with an invariant! This is not hard to do, since we know a few properties of the new invariant:
One might be tempted to guess
$\Delta r^2=\Delta x^2+\Delta y^2+c^2\Delta t^2$
but that doesn't work, and our example above with the mirrors in the moving frame is an illustration: as the velocity increases, both the spatial and the temporal intervals will increase (they have to in order to make the speed of light constant). So adding everything like the above can't be an invariant because it just gets bigger as the relative velocity $v$ approaches $c$.
So why not add a minus sign somewhere? Since the time component $\Delta t$ will
have $c$ as a multiplier, and that's a big number ($c=3\!\times\!10^8$m every second!!!!)
we can try taking the temporal part and subtracting the spatial part, like this:
$$\Delta r^2=c^2\Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2\label{eq9}$$
(we added $\Delta z^2$ since in fact there are 3 spatial dimensions!)
To check this, we substitute for each of the &Delta's using equations
(\ref{eq4pp})-(\ref{eq6pp})
(with a corresponding equation for the variable z). What you should be able to
verify is that
$c^2\Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2=
c^2\Delta t'^2-\Delta x'^2-\Delta y'^2-\Delta z'^2$
Brief aside on c | Back to top |
But this is not very accurate! The distance between the poles is hard to define since the actual location of the poles can change, and the shape of the earth can change, all due to gravitational and geophysical effects. And the length of a day is something that can also change from some of the same effects as above. An alternative approach, and in fact the approach used today, is to first accurately define the unit of time (aka second) to be the duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom (see http://www.bipm.org/en/publications/si-brochure/second.html).
Once you have the second well defined, and the above definition is exceedingly accurately determined using atomic clocks (gadgets that are accurate to 1 second in 100,000,000 years), then we need to define the meter. Here's what we do now: we decide that the speed of light is exactly 299,792,458 meters/sec, so the meter is defined by definition as the length that a beam of light travels in 1 second. But for most earthly purposes, $c=3\!\times\!10^8$m/s is quite good enough.
It's useful to have a feel for the speed of light in other units. One of the most useful to physicists is $c=.3$m/nsec, or an even more useful value is $c=1$foot/nsec (1 nsec is 1 billionth, or $10^{-9}$, of a second}. That's pretty approximate, but it's very useful if you have to deal with electronics (signals propagate at around $\frac{1}{2}c$ or $\frac{2}{3}c$.
Another useful way of quantifying $c$ is in the area of electromagnetic waves, where we know that the frequency $\nu$ and wavelength $\lambda$ are related by $c=\lambda\nu$. Rewriting $c=0.3$m/s as $0.3$m$\times\!10^9$/sec or $c=1$foot$\cdot\!1$GHz. This is very useful in any field where we have to convert from wavelength to frequency fast. For instance, the average FM signal is around 100MHz=0.1GHz, so that tells you the wavelength is around 3ft (wavelent in feet times frequency in GHz have to come to $0.3$ when multiplied together), whereas the average AM signal is around 1MHz=0.001GHz, requiring a 300ft wavelength. This is why you can get FM signals in cities and under bridge overpasses on highways, but not AM signals - the FM signals will "fit" whereas the AM signals have a harder time (this has to do with diffraction but that's another story).
Lorentz Contraction | Back to top |
We then discovered the concept of time dilation by considering a process where two events occur in $O'$ at the same location in that frame, which means $\Delta x'=0$. We can then use equation (\ref{eq6pp}) to find the corresponding time difference in $O$, and that gave us the time dilation equation (\ref{eq7}) ($\Delta t=\gamma\Delta t'$) relating the proper time (here $\Delta t'$) to the time in any other frame that is "boosted" along with velocity $\beta$. Perhaps a more useful equation is: $$\Delta t = \gamma\Delta\tau\label{eq10}$$ where $\tau$ is the proper time.
Now we want to investigate an analogous situation where this time, the two events occur at the same time (simultaneously) in one frame, and compare the spatial intervals between the two frames to see the effect. It is worth being very careful here, so let's set up the experiment: there are two frames, $O$ and $O'$ that are moving with some relative velocity $v$, and in one of the frames, there is an object that we want to consider. The frame of the object is called the proper frame of the object, just like in the time situation, and what we want to do is to make a measurement of the length of the object by an observer in $O'$ (the proper frame), and by an observer in frame $O$. For simplicity, let's assume the length we want to measure is the length of the object along the axis of motion $x$ so that we don't have to worry about the transverse directions $y$ and $z$. The situation is as depicted in the simulation below:
In the simulation below: click to run the simulation, to pause, and to reset it.
When we measure anything, what we are doing is writing down the space-time coordinates $(x,t)$ of the endpoints of the object in our frames. So the person who is sitting in $O'$ will write down $(x'_1,t'_1)$ and $(x'_2,t'_2)$, and the person who is sitting in $O$ will write down ($x_1,t_1)$ and $(x_2,t_2)$. The lengths they are measuring will simply be given by the difference in the spatial coordinates: $L' = \Delta x' = x'_2-x'_1$ and $L = \Delta x = x_2-x_1$ in the two different frames.
Because the object is not moving relative to the observer in the proper frame (pretty much by definition!) the difference in the time coordinates $Delta t'= t'_2-t'_1$ is irrelevant, because it doesn't matter if you write down the value of $x'_1$ on monday and $x'_2$ on tuesday, since the object is not moving (relative to the observer in that frame, the person doing the measuring). But since space and time are mixed up into a space-time, what we want to do is to see what someone who is not in the proper frame would measure for the length, and to do so we want to keep the coordinate $t'$ out of the calculation. This is pretty straight-forward, as you will see.
What will the observer in $O$ (this is the "lab" frame, and the moving frame $O'$ is moving with velocity $\beta$ in $O$) measure as the length $L'$ of the blue ruler, which is stationary in $O'$? That's an easy experiment: as the blue ruler goes by, the observer in $O$ will mark the endpoints using a ruler (the black one) that is stationary in $O$. What does this mean "mark the endpoints"? It means that the stationary person in $O$ will record the $x_1$ and $x_2$ coordinates at the same time, and the length $L$ measured will be given by $L = \Delta x = x_2-x_1$. Perhaps you can see where the interesting physics is here: the concept of at the same time is our (now relative) concept of simultaneity, and since the observers in $O$ and $O'$ will not agree on what was simultaneous in $O$, then they will also not agree on the lengths measured in those frames.
If you run the simulation now, note that the blue arrows mark the position of the blue ruler as measured by the stationary ruler (and leaving a dashed image of the ruler), with each point recorded at the same time in frame $O$.
Lets do the calculation now. What we know is that the events of measuring the positions in $O$ occur at the same time in $O$, so we have \delta t=0. We could use equations (\ref{eq4pp})-(\ref{eq6pp}), but it isn't going to be all that useful to make use of $\Delta t=0$ there. However, if we construct the inverse transformation, where we write down the coordinates in $O'$ as a function of those in $O$, we would get equations (\ref{eq4p})-(\ref{eq6p}) back, and then construct the corresponding difference equations to get: $$\Delta x'=\gamma(\Delta x-\beta c\Delta t)\label{eq4ppp}$$ $$\Delta y'=\Delta y\label{eq5ppp}$$ $$\Delta z'=\Delta z\label{eq6ppp}$$ $$c\Delta t'=\gamma(c\Delta t-\beta \Delta x)\label{eq7ppp}$$ Equation (\ref{eq4ppp}) is what we want: we can use $\Delta t=0$ and get $$\Delta x'=\gamma\Delta x\label{eq11}$$ or equivalently, $L=L'/\gamma$. That is, the length measured in any frame will be smaller than the proper length by a factor of $\gamma$. This is the famous Lorentz contraction.
So to summarize, due to the fact that space and time are no longer independent, and that space and time are mixed up from one frame to another, there is no such thing as absolute simultaneity, and this means that there exists:
| Time Dilation | $\Delta t=\gamma\cdot\Delta t_{proper}$ | ||
| Lorentz Contraction | $\Delta x=\Delta x_{proper}/\gamma$ |
Or in words, time intervals are shortest, and space intervals are largest, in the proper frame relative to any other reference frame.
Is this really true or is this an artifact of some mathematics? How do we understand the time dilation and Lorentz contraction? It's pretty weird! But let's go back to the example of the muon that lives long enough in frame $O$ to be seen on the surface of the earth, even though in frame $O'$ (the muon's proper frame) it only lives on average 2 millions of a second. What happens in the rest frame of the muon? In the muon's rest frame, it sees the earth's surface rushing up at it. If the muon were to measure the depth of the earth's atmosphere, it would measure the proper length divided by the Lorentz factor $\gamma$ - it would measure a Lorentz contraction of the earth's atmosphere (the thickness of it). So from the muon's perspective, it still only lives 2 millionths of a second in its reference frame, and so it would not expect to live long enough to traverse a distance of 10s or 100s of km. But from its proper frame, it sees the surface of the earth moving towards it with some large velocity, and via the phenomena of Lorentz contraction, the atmosphere is "thinning" by an amount $\gamma$, the same factor for the time dilation as measured from someone in the rest frame of the earth.
There's another very interesting manifestation of Lorentz contraction: magnetic fields due to currents in wires, and the force on a moving test charge. To see this in the context of relativity, keep in mind that metallic wires are electrically neutral to great accuracy. A current in a wire consists of negative conductive electrons (around 1 per atom in most metals) moving along the wire. Imagine the situation where the test charge is positive, moving parallel to the wire in the same direction as the electrons, and consider the Lorentz contraction of the spacing between the electrons in the wire, and the spacing between the positive ions in the wire. The test charge and the electrons are in the same reference frame, but from the point of view of the test charge, the positive ions are moving in the opposite direction. Therefore the spacing between the positive ions is Lorentz contracted, which causes a higher positive charge density (linear density) than the negative linear density. Thus a positive force on the positive test charge and it's deflected away from the wire. If you work out the right hand rules, you will find that this is exactly what a vxB force would do - the Lorentz contraction is surely real!
Let's return to the above simulation, of a moving blue ruler being measured by a ruler in another frame. If the act of measuring involves a simultaneous measurement in $O$, then that means the observer in $O'$ would cry out that it's unfair, that the person in $O$ is not measuring the endpoints at the same time, and of course that's why they get a different answer for the length! We can easily calculate what the observer in the blue ruler's proper frame would measure for the time difference of the measurement by the observer in $O$ using equation (\ref{eq6ppp}):
$c\Delta t' = \gamma (c\Delta t-\beta \Delta x) = \gamma(-\beta \Delta x) = -\beta \Delta x$
So the person in $O'$ will see a negative time interval for the measurement interval in $O$, which means that it will see the measurement made on the near side of the ruler first, then the far side. (Remember that the frame $O$ is moving along the $-v$ direction here.) And the time difference $\Delta t'$ will be given by the Lorentz contracted length as measured by the observer in $O$ times the boost velocity $\beta =v\!/\!c$. Keep in mind, of course, that the time difference $\Delta t' = -\beta \Delta x/c$ will be exceedingly small since $c=3\!\times\!10^8$!
Energy and Momentum (starting with energy considerations) | Back to top |
$\delta E = mv\cdot \delta v$
which means that as $\delta E\to \infty$, $v\to\infty$ which violates the postulates of relativity. Clearly, we need to change what we mean by energy especially in the relativistic limit of $\beta\to 1$.
There are several ways to understand this problem in Newtonian kinematics. One way is to first consider the deBroglie relations:
$E=h\nu$ and $p=h\!/\!\lambda$
For photons, where $m_\gamma=0$, we have $E=pc$, or in units of $c=1$, $E=p$. Extending this to particles with $m>0$, we have to rethink what we mean by "energy", and the key is to take account of the mass. What Einstein did in 1905 was to calculate the energy radiated by an electron in two different reference frames, taking into account the Lorentz) transformations as deduced from applying the principle of relativity. One tricky way that takes into account what Einstein already learned is to alter equation (\ref{eq12}) to be: $$\delta E=\frac{p}{E(m)}\cdot\delta p\label{eq13}$$ keeping the units $c=1$, showing explicitly that $E=E(m)$, is a function of the mass $m$, and taking into account that in the "non-relativistic" limit of $\beta ≪ 1$, equation (\ref{eq13}) has to reduce to (\ref{eq12}).
Given that, equation (\ref{eq13}) can be rewritten $E\cdot\delta E = p\cdot\delta p$ which means that $E^2 = p^2 + K^2$ where $K^2$ is some unknown constant of the integration. In the limit where $p$ is "small" ($p/K\to 0$), we would have as the lowest order approximation
$E = K + p^2/2K$
This is an amazing equation and tells us a lot! It tells us that we can equate $K$ with the mass $m$, that $E=m$ when $p=0$, and that in general we have the equation $$E^2=p^2+m^2\label{eq14}$$ In the above, the variable $m$ is simply a number, not a function of momentum or of energy, but a constant that is also referred to as the "rest mass" of a particle. It is the also the energy of the particle in the reference frame of the particle, also known as the particle's $proper frame$.
One would imagine that the Lorentz transformations should apply to any object legitimately defined in 3-space with a "time" component (such as $t,x,y,z$, and we look for a way to transform the energy $E$ and the momentum $(p_x,p_y,p_z)$. A clue as to how to construct such an energy-momentum 4-vector is to note that all 4-vectors have to have an invariant, just as for the case of position 4-vectors, the invariant is $R$ is given by $R^2 = t^2-x^2-y^2-z^2$ (we are setting $c=1$ here). But we just derived an invariant: the rest-mass of a particle should be the same as measured in any reference frame! So if we use as the invariant $m^2 = E^2-p_x^2- p_y^2-p_z^2$ then we should be on safe ground to construct the 4-momentum as $(E,p_x,p_y,p_y)$, and so the Lorentz equations for boosts along the x-direction would be: $$p_x'=\gamma (p_x-\beta E)\label{eq15}$$ $$p_y'=p_y\label{eq16}$$ $$p_z'=p_z\label{eq17}$$ $$E'=\gamma (E-\beta p_x)\label{eq18}$$ and the corresponding reverse transformation $$p_x=\gamma (p'_x+\beta E')\label{eq15p}$$ $$p_y=p'_y\label{eq16p}$$ $$p_z=p'_z\label{eq17p}$$ $$E=\gamma (E'+\beta p'_x)\label{eq18p}$$ Let's check this by considering the decay of particle (1) into two particles (2) and (3): 1→2+3. First, it's convenient to use the notation for a 4-vector as $p^\mu =(E,p_x,p_y,p_y)$ where the index $\mu $ runs from 0 to 3, $p^0=E$ and $p^{1,2,3}=p_{x,y,z}$. Let the frame $O'$ be the $proper frame$ of the particle, which would mean that we would have $E'=m$ and $\vec p\!'=0$ in that frame, or in our notation $p'^\mu =(m,\vec 0)$. In the lab frame where we measure the momentum of the two "daughter" particles, we would have
$p^\mu_2=(E_2,\vec k_2)$ and $p^\mu_3=(E_3,\vec k_3)$ where we understand that the 2nd component $\vec k$ means $p_x,p_y,p_z$.
We can now make use of the postulates of relativity and the property of invariants to get $m^2=(E_2+E_3)^2- (p_{x2}+p_{x3})^2- (p_{y2}+p_{y3})^2- (p_{z2}+p_{z3})^2$
This can be easily checked by particle physicists measuring such things as for example the decay $\psi\to\mu^+ \mu^-$ where we measure the 4-momentum of the 2 muons and see if they form the "invariant mass" of the neutral $\psi$ meson. As you can imagine, this has been verified to a very high precision for any measurable decay in such experiments, and particle physicists have tested special relativity to great accuracy.
Energy and Momentum (starting with velocity) | Back to top |
$\vec v=\frac{dx}{dt}\hat i+\frac{dy}{dt}\hat j+\frac{dz}{dt}\hat k$
We can also start with defining a 4-velocity $u^\mu$ (and this will become very useful when we get to general relativity later) based on the rate of change of coordinates in the proper frame, with respect to the proper time: $ds^\mu\equiv(dt,dx,dy,dz)$ and then $u^\mu\equiv\frac{ds}{d\tau}= (\frac{dt}{d\tau},\frac{dx}{d\tau},\frac{dy}{d\tau},\frac{dz}{d\tau})$
We can then relate the infinitesimal change in proper time $\tau$ to the time $t$ in any frame via the time dilation factor (equation (\ref{eq7})): $d\tau=\frac{dt}{\gamma}$, which gives us the 4-vector $u^\mu=\gamma(c,\vec v)$ where we have used $c$ explicitly here. Such a 4-vector has as it's relativistic invariant $u^\mu u_\mu = c^2$. We can then form the 4-momentum analogous to the nonrelativistic $p=mv$:
$p^\mu=mu^\mu=(\gamma mc,\gamma m\vec v)$
Keeping track of units is sometimes important. Let's multiply the 4-momentum by $c$ so that it has units of energy, and write:
$cp^\mu=(\gamma mc^2,\gamma mc^2\vec\beta\!)$
We can now equate the energy with the time component, $E=\gamma mc^2$, and the momentum with the spatial vector $\vec p=mc\gamma\vec\beta$, with the same relativistic invariant: $E^2=mc^2+(pc)^2$ as above.
$E=mc^2$ | Back to top |
$0 = \gamma (p - \beta E)$
Here we are assuming that the particle moves along the x-axis, so $ p_{y,z}=0$ and all the momentum is along the $x$-axis.
This equations gives us the important relation $$\beta = \frac{p}{E}\label{eq19}$$ or $p = \beta E$, as opposed to $p = mv$ for Newtonian. If we were to go back to units where $c=3\times 10^8$m/s, we would have $pc = \frac{E}{c}v$ vs $p = mv$. That might lead you to think all you have to do is equate the two, and get $\frac{E}{c^2} = m$ , or the famous formula $E=mc^2$ .
But this is clearly wrong, because in frame $O$ the particle is moving with some non-zero momentum $p$, so how could $E=mc^2$ and also satisfy equation (\ref{eq14}) ($E^2=p^2+m^2$)? The right way to do it is to consider equation (\ref{eq18}) just like you considered equation (\ref{eq15}) and set $E'=mc^2$ (which is true in $O'$ since the particle is stationary there):
$E'=mc^2 = \gamma (E - \beta pc)$
and substitute $pc=\beta E$ for $\beta$, and use equation (\ref{eq14}). This should give you the formula $$E=\gamma m c^2\label{eq20}$$ and the sister equation using (\ref{eq19}) to get $$p =\gamma \beta m c\label{eq21}$$ This equation tells us a lot! We know that as we pump energy into a particle, the velocity will increase but $v\lt c$ , so as the velocity approaches $c$ , the factor $\gamma\to\infty$. If you add energy, then the energy and momentum will increase, but not the velocity, at least not at the same rate! It can't! The above equations are telling you what happens as you pump energy in.
Why do we keep seeing $E=mc^2$ ? This equation certainly cannot be true when the particle has any momentum, however the equation is exactly true in the $ proper frame$ of the particle, and so we can call $ m$ the $ rest mass$ because it is clearly meant to denote the mass as an absolute quantity, regardless of motion (no matter how something is moving, you can always, boost into it's proper frame where the momentum is zero).
One way to think of this equation is that in the proper frame, the energy of the particle is entirely tied up in the particle's mass. The power of $E=mc^2$ is in the energy equivalence of mass, and this is certainly born out in nuclear explosions. In WW2, Hiroshima Japan was subjected to a Plutonium bomb where approximately 700 mg ($0.7\times 10^{-3}$kg) of mass was converted to energy. Using Eistein's famous formula, that released $E=0.7\times 10^{-3}\cdot(3\times 10^8)^2=63\times 10^{12}$ joules of energy. That is a very large amount of energy, equivalent to 17.5 million kilowatt hours, or the amount of energy from a 2-gigawatt power plant for an entire year.
Physicists also sometimes use the equation $ E =Mc^2$ and $M\equiv \gamma m$. Here the mass $M$ will increase as the velocity increases and gets closer to $v=c$ . Sometimes physicists say that as particles become "relativistic", their mass increases, but it's really not a very accurate statement. One can never measure the rest mass of something without being in its proper frame, and when the particle is moving then you are measuring momentum and energy. As you add energy to a particle, it can't realize an increase in the velocity past the speed of light, so what does the energy you keep adding do if not make the particle go faster? One can argue that that added energy increases the mass, but it is much more accurate to say that the added energy increases the momentum. It's thinking that $ p=mv$ that gets you into trouble!
One last interesting aside: if a particle has no mass, then $E=p$ . This is consistent with $\beta =\frac{p}{E}=1$,$\gamma\to\infty$, so we cannot use $p=\gamma mv$. Evidently the correct way to think of momentum is via equation (\ref{eq21}): instead of $p=mv$ we can use $p=Ev$ where $E$ is the relativistic energy, reducing to $E=mc^2$ (or $E=m$ with units $c=1$) in the proper frame.
Relativistic Doppler | Back to top |
In the case of light, we can derive a relativistic doppler frequency shift by taking advantage of two important things:
Using equation (\ref{eq18}), we have
$E_o=\gamma (E_s-\beta p_s)= \gamma E_s(1-\beta )$
Applying equation (\ref{eq7p}) for $\gamma $ we have
$\frac{E_o}{E_s}=\sqrt{\frac{1-\beta}{1+\beta}}$
Applying $E=hf$ gives us our doppler frequency shift: $$\frac{f_o}{f_s}=\sqrt{\frac{1-\beta}{1+\beta}}\label{eq23}$$ This describes the frequency observed by an observer that is moving with velocity $\beta $ away from the source (trying to out-run it). The number under the square root will always be less than 1, so the frequency is shifted down, or "into the red" (considering visible light). What about the situation where the source is moving away from the observer as opposed to the observer moving away from the source? It's all relative, and doesn't matter!
Astronomers ofter refer to distances in terms of a "red shift". This is because in the standard model of cosmology, the entire universe is expanding, and one can relate the distance between any 2 objects to their relative velocity ("Hubble's Law), which again determine the dopper shift. In astronomy, the red shift $z$ is defined by
$1+z=\frac{f_s}{f_o}=\sqrt{\frac{1+\beta}{1-\beta}}$
$z$ measures "cosmological distances" as determined by red shifts using Hubble's law. Objects that are greater than $z=0.1$ have velocities that are dominated by cosmological expansion (as opposed to random moving inside galaxies, or galaxy rotation, etc).
If one solves the above equation for $\beta$, one gets
$\beta = \frac{(1+z)^2-1}{(1+z)^2+1}$
which approaches 1 rather quickly (for $z=2$, $\beta =0.8$ which is a pretty large velocity for something as large as a galaxy! Given the finite value for $c$, we know that the further away something is, the further back in time we are looking when we see it. As a reference, the highest red shifts observed are around $z=8.6$, which corresponds to an object that existed at around 600 million years after the Big Bang. The most distant quasar has a red shift at around $z=7.6$, and so on. These are exceptionally distant objects! Note that the nearest galaxy, Andromeda, is approximately 2.5M light-years away, has a shape similar to our Milky Way galaxy, about 220,000 light-years across, and has around a trillion stars (roughly twice the number of stars in our galaxy). The red shift of Andromeda is essentially zero, in fact it's a blue-shift as the relative velocity is dominated by local galaxy movement. The cosmological microwave background (CMB) radiation has a redshift of $z=1089$, which means we are seeing it as it existed around 380,000 years after the beginning of the Big Bang (380,000 out of a total of 13.8 billion years, the current measurement for the age of the universe).
Space-time Diagrams | Back to top |
In space-time, we deal with "events" as having 4 coordinates: 3 spatial, 1 temporal. As noted in equations such as (\ref{eq4})-(\ref{eq6}), the spatial and time coordinates are mixed up, but not completely: the coordinates transverse to the direction of motion remain unchanged when the reference frame is boosted. So it's really the longitudinal (longitudinal, along the direction of motion) and time coordinates that are mixed up, and this suggests we look at an "x vs t" plot to see if we can understand the Lorentz transformations visually. Actually for historical reasons (and some not very important technical reasons), we show the plot as "t vs x" instead of "x vs t" (see the diagram below).
The velocity of a particle is given by the ratio of the distance $\delta x$ traveled over a time interval $\delta t$, and if you were to plot distance along the vertical and time along the horizontal, the velocity would be the slope of the curve (for constant velocities, the curve would be a straight line). In our space-time plot, since we are plotting time along the vertical and distance along the horizontal, the velocity would be the inverse of the slope of the curve. This should be pretty easy to picture - a particle that has stopped will be at constant position (constant "x"), and with time ticking on, the curve that traces out such a path would be vertical with an infinite slope.
Interestingly, a particle at constant time would trace out a horizontal line parallel to the x-axis. Such a particle would be traveling at an infinite velocity - this is not allowed! If we use units of $c=1$, then the fastest velocity would be $v=1$, which means a line with a slope of 1: $\delta x = \delta t$.
Let's look at all the features of this new picture (in the diagram below, click "Toggle $c$" now). The dashed blue lines show the path of a beam of light, bisecting the x and t axes at 45° ($x=t$). The dashed lines go through the origin ($x=t=0$) by construction: in the proper frame of the particle, it is standing still so we can set $x=0$ and it will stay that way. Time, however, always keeps marching on even in the proper frame, and so the origin represents a particular space-time event for this particle. The beam of light could be going from the origin towards positive or negative positions, so we need to draw 2 bisectors. And since the beams come from the past and go into the future, they have to cover times for which $t\lt 0$. So the upper yellow part shows the positions of all points in space-time that a particle at the origin at t=0 could conceivably reach if it could go fast enough, but never faster than light. That's why all of the yellow positions are following $v\lt 1$, or $x \lt t$ (remember, $c=1$) and represent the future (of that particle at our origin). The bottom yellow area shows all of the positions that could have gotten to the origin of our plot with $v \lt 1$, so it represents the past.
Now what we want to do is to understand what Lorentz transformations look like in terms of
space-time curves.
Let's start with the stationary reference frame $O$, and the moving frame $O'$
just like in the section above (moving with velocity
$\beta$ along the $x$ axis). The equations relating
position and time between the two frames are the same equations (\ref{eq4})-(\ref{eq6}) above,
and the inverse equations (\ref{eq4p}-\ref{eq6p}),
where we are using the units where $c=1$.
Let's start with an easy straightforward question:
What are the locus of all points in O that are at
a constant position x' in O'?
Or in other words, if we have a curve in $O'$ where all of the points are at a constant
position, how does the curve transform to $O$?
Of course in frame $O'$, that locus
would be a vertical line - and so would could represent the $t'$ axis - but we want
to see the space-time curve in frame $O$,
since we we know that space and time are "mixed up" in going from one reference frame
to another.
An easy way to answer this question is to start with equation (\ref{eq4p}) and form the difference
equation:
$\delta x' = \gamma (\delta x - \beta \delta t)$
If $x'$ is constant, then $\delta x'=0$ and the above reduces to the equation
$\delta x = \beta \delta t$
This is clearly a straight line with slope $\beta $, or in the $t-x$ plane,
a straight line with slope $1\!/\!\beta$. (Click the button labeled
"Toggle $x$" above to see such a line drawn in red onto the space-time plot above.
Note that $\beta$ is set arbitrarily to 0.2 here.)
Similarly, we can ask for the locus of all points in $O'$ that represent space-time
events that occur at the same $t'$ in $O'$ (the $x'$ axis),
and see the space-time curve in $O$.
To understand such a curve, we can use a difference equation based on (\ref{eq6p}):
$\delta t' = \gamma (\delta t - \beta \delta x)$
and set $\delta t'=0$ (constant $t'$) to get the equation
$\delta t = \beta \delta x$
This is another straight line, this time with slope $\beta $ in the $t-x$ plane.
Click the button labeled
"Toggle $t$" above to see such a line drawn in red onto the space-time plot above.
(Also, $\beta$ is set arbitrarily to 0.2 here.)
A few things worth pointing out here:
What do events that are simultaneous in $O'$ look like on the space-time plot of
frame $O$?
Simultaneous means that they all happen "at the same time" (in that frame).
That means that the time $t'$ is constant, no longer a variable, and that simplifies
the Lorentz equations tremendously. To see this, start with equations (\ref{eq4}) and
(\ref{eq6}), holding
$t'$ as some constant number, eliminate $x'$, and solve for $t=t(x)$.
When you do this, you should get the following interesting equation:
$t = \beta x + t'$
This equation is completely understandable: if we are considering frames where the
relative velocity $\beta $ is very small, even 0, then we get $t=t'$ as we
should.
If we consider simultaneous events in $O'$ where we set $t'=0$, then we
recover the boosted $x'$ axis as derived above.
As we change $t'$ to some other arbitrary value, the higher the value the higher
the "y-intercept" of the function $t(x)$, but the slope is the same: $\beta $.
This makes perfect sense - after all, $O'$ is moving with velocity $\beta $
with respect to $O$!
The following simulation generates a bunch of random points $x'$ (in yellow), with a fixed
$t'$ and boost $\beta$, both programmable (use the sliders below).
You can get a good feel for the idea of simultaneity by playing with the parameters.
The button labelled "World Lines" will draw the world line of each point (in red),
which would be
a straight line along the $O'$ axis (just like if it were a world line in $O$
it would be a vertical straight line). Each world line is at a constant value of
$x'$ in $O'$ but has a slope in $O$ parallel to the $t'$ axis.
Before leaving this subject, it is interesting to consider space time curves relative to
the speed of light $c$. Since the principles of relativity tell us that $c$
is the maximum velocity in space-time, we should consider characterizing space-time
intervals according to whether the slope $\delta x\!/\!\delta t$
is greater or less than $c$ (or $1$ in the units $c=1$).
The former are called "space-like", and the latter "time-like". Why these names?
Because for paths that are space-like, you could always boost into a reference frame
where the entire interval is along the $x$-axis, and for paths that are time-like,
you could always boost into a reference frame (the "proper frame") where the entire
interval is along the $t$-axis. One can restate the principle of relativity to
say that objects are only allowed to follow time-like curves.
Barn and Ladder Paradox | Back to top |
Both of the barn doors are closed (thick blue lines). The ladder is clearly longer than the length of the bard along the ladder's "direction", so one can conclude that the ladder will not fit inside the bard.
Now comes the paradox. Let the barn be in the $O$ frame, and the the ladder is in frame $O'$ moving along the $x$ axis (here left to right) with velocity $\beta$. In frame $O$, an observer would measure the ladder to be "smaller" along the $x$ axis by an amount $\gamma $ from the Lorentz contraction. That person would conclude that it is indeed possible to have the ladder completely enclosed inside the barn. But the person in frame $O'$ who is running with the ladder would see the barn moving towards them with velocity $\beta $, and so would measure the barn to have a length that is also Lorentz contracted by the same amount $\gamma$. That person would conclude that there's no way the ladder can fit inside the bard! Such is the paradox, and such is the power of space-time diagrams to resolve it!
The key to understanding the paradox has to do with the idea of simultaneity, since being "entirely inside the barn" means that the ladder is inside the barn with both doors closed at the same time.
Below, we can draw the space-time situation for the ladder and the barn, reviewing what we've learned about how to visualize the Lorentz transformation.
The $x'$ and $t'$ axes are drawn in dashed lines. The barn is an object that is not moving with respect to $O$ (it is stationary in $O$) so we draw the world lines of both sides of the barn as vertical dotted blue lines. The ladder, which has a proper length that is longer than the width of the barn (as above) is stationary in $O'$, so we draw the endpoints as dotted red lines with slope $\beta $: parallel to the $t'$ axis. Now comes the important part: what we mean when we describe the situation where the ladder is completely inside the barn is that we can have both doors closed at the same time (in $O$, the proper frame of the barn) with the ladder inside the barn. Let's define "front" and "back" of the ladder relative to the direction of motion, which is along increasing $x$, and the same for the barn. We set up the initial situation where the front door of the barn is closed, and the back door is open - so the ladder can enter the barn front side first. Just at the point where the front of the ladder is about ready to crash into the front door (which is initially closed), we look to see where the back of the ladder is. If it's between the blue horizontal lines, that means that we can close the back door, the ladder is completely inside the barn, and then we can open the front door to let it keep going before it crashes into the door! In between the blue lines means that we note the coordinates of the back side of the ladder, which means that the front and back are both at the same time $t$ - they are "simultaneous", which of course is relative. But what this amounts to is look at where the world line of the back of the ladder intersects the simultaneous world line of the observation (made at constant $t$), and if that intersection is between the blue horizontal lines, the ladder is inside the barn with both doors closed. This horizontal line is drawn in yellow.
You can play with the simulation and change the velocity $\beta $ and see that unless the ladder is going fast enough the Lorentz contraction is not great enough to have both doors closed at the same time in $O$ (the default value of $\beta =0.25$ is not fast enough!) The trick is to increase the velocity so that the horizontal yellow line is completely between the vertical blue lines. But the bottom line is that the ladder $can$ fit into the barn, because of the relativity of simultaneity - the person in frame $O$ will say that both doors were shut at the same time with the ladder inside, whereas the person in frame $O'$ will say that the ladder entered the barn with the front door shut, then the front door opened, the ladder moved and poked out of the barn with the back inside the back door, and $then$ the back door shut: the back door shut at a $later$ time $t'$ (in $O'$)! Relativity of simultaneity makes things weird!
Proper Time (and the "Twin Paradox") | Back to top |
Let's start with 2 events in frame $O$. Event 1 is at coordinate ($x_1,t_1$) and event 2 is at coordinate ($x_2,t_2$). We can then define the intervals $\delta x = x_2-x_1$, $\delta t = t_2-t_1$. Now let's introduce frame $O'$, moving with velocity $\beta $ with respect to $O$ along the $x'$-axis, and that the two axes $x$ and $x'$ are parallel. From the point of view of an observer in $O'$, the two events will be measured to be at coordinates ($x'_1,t'_1$) and ($x'_2,t'_2$), and similarly we can define the intervals $\delta x' = x'_2-x'_1$, $\delta t' = t'_2-t'_1$. We know that the relationship between an event in $O$ and $O'$ is given by the Lorentz equations:
$x=\gamma(x'+\beta t')$
$t=\gamma(t'+\beta x')$
We also know that there is an invariant $\delta R$ such that
$\delta R^2 = \delta t'^2-\delta x'^2-\delta y'^2-\delta z'^2$
From considering the very specific case where the events in $O'$ occur such that $\delta x' = 0$ (in the same place in $O'$), then $O'$ is the proper frame, and $\delta\tau = \delta t'$ is the proper time. And, the relationship between $\delta\tau$ and $\delta t$ is given by the equation $\delta t=\gamma\cdot\delta\tau$, which means that the time interval between events is minimal in the proper frame. This minimal time, the time in the proper frame, is called the proper time and the above equation demonstrates the phenomena called time dilation.
We can calculate the relativistic invariant in the frame $O'$ where the position does not change ($\delta x'=0$, and ignoring the $y'$ and $z'$ coordinates):
$\delta R^2 = \delta t'^2 - \delta x'^2 = \delta t'^2 \equiv \delta \tau^2$
Since the relativistic invariant $\delta R$ is the same no matter which reference frame you choose, which means that we could also use frame $O$ to get:
$\delta R^2 = \delta t^2 - \delta x^2$
which means that $\delta\tau^2=\delta t'^2 - \delta x'^2 = \delta t^2 - \delta x^2$
This is the origin of the common notion that the proper time is the relativistic invariant, which is accurate if you define the proper time as the time in the frame where the object is not moving.
Note that in full 4-dimensional space, we can write the infinitesimal proper time interval $d\tau$ as
$d\tau = \sqrt{dt^2 - dx^2 - dy^2 - dz^2}$
What is clear, however, is that straight time-like paths (see above) maximize the time interval $\delta t$ (the "proper time" as defined in this section).
As an example, consider the situation of two observers, one in $O$ and the other in $O'$, and $O'$ moves with a velocity $\beta _+$ relative to $O$ along co-parallel $x$-axes. The observer in $O'$ sits in some kind of space-ship, so the position $x'$ in $O'$ doesn't change - all space-time motion in $O'$ is along the $t'$ axis. The spaceship goes along for a time $\delta\tau$ and turns around, and the return velocity $\beta_-$ is the same as $\beta_+$ only in the opposite direction (in $O$): $\vec{\beta_-}=-\vec{\beta_+}$. Let's set the situation such that the spaceship eventually turns around and comes back to the starting place, and the velocity of the returning $O'$ is the same as the initial $O'$. This is the famous "twin paradox", and the space-time diagram is shown directly below.
In the figure below, we see the path of the spaceship: it starts at the origin ("A"), and moves with velocity $\beta $ for some time $\delta t'$ (as measured in the frame of the spaceship, $O'$) reaching point "B". At that point, the spaceship turns has to decelerate to $\beta =0$ (in $O$), turn around, and accelerate back up to $\beta $ heading back to the origin, $x=0$. (Note: the deceleration would leave the spaceship world line as a vertical line in spacetime, but this is not shown - we just reverse direction at point "B").
As you can see in the diagram, $\delta t'$ is the "distance" from A to B along the $t'$ axis, $\delta x$ is the distance along the horizontal $x$-axis, and $\delta t$ is the "distance" along the vertical $t$-axis.
The units here are $c=1$, which means 1 second of time is equivalent to $3\times 10^8$m, or 186,000 miles. What we can see is that given an initial velocity starting at $\beta =0.25$ (and changeable via the blue arrows), for every 50 years of time that the person in the spaceship in $O'$ spends, the person in $O$ ages 51.64 years. If you increase the velocity to $\beta =0.95$, when the astronaut returns, everyone in $O$ will be over 158 years older. So if the astronaut has a twin who is left behind, and when the journey starts the two are 20 years old, when the astronaut returns he will be 120 and the twin, if still alive would have been over 178 years old. Note that in this case, the spaceship would have had to have traveled a distance of 12.9 light-years. Alpha Centauri is around 4.35 light-years from earth, Sirius A is 8.6, and given the density of stars near the sun to be at about 0.004 per cubic light-year, there should be around 36 stars within 12.9 light-years.
(Note: The total energy of a space ship moving at a velocity of $\beta =0.95$ would be given by $E=\gamma mc^2$, and the kinetic energy would be the total minus the rest mass energy: $KE=(\gamma -1)mc^2$. At $\beta =0.95$, $\gamma =3.20$, and if the spaceship is even as small as 1000kg (about 1 ton, the size of a VW bug), you would need around $2\times 10^{20}$ joules, or about $5.5\times 10^{14}$kW-hr, or over $6,000$GW-years. Note that 6,000 GWatts is almost twice the total amount of power consumed by humans in 2010.)
This phenomena is called the "twin paradox". The paradox part comes from the fact that along each leg A→B and B→C, each observer would measure the same time dilation effect. So in frame $O$, the observer would measure the clock in frame $O'$ to be "slower", and the observer in $O'$ would measure the clock of the person in $O$ to be "slower" (time dilation), yet after the end of the round trip clearly the clocks are different. And of course, the resolution of the paradox comes from realizing that the two frames are not equivalent - at point B, the spaceship decelerates such that it is no longer moving with respect to an observer in $O$, turns around, and accelerates back to velocity $\beta $ moving towards the observer at point A in $O$. The observer in $O$ never decelerates or accelerates at any point. And this makes all the difference, resolving the "paradox".
| Along: | $\delta t'=\delta\tau$ | $\delta x$ | $\delta t$ |
|---|---|---|---|
| A→B: | 0 | 0 | 0 |
| B→C: | 0 | 0 | 0 |
| A→C: | 0 | 0 | 0 |
Prelude to General Relativity | Back to top |
It is interesting to write the space-time invariant definition equation (\ref{eq9}) for intervals in terms of some kind of sum over the components of the interval 4-vector:
$\delta x^\mu\equiv(\delta t,\delta \vec{x}\!)$
The invariant is given by:
$\delta R^2 = \delta t^2-\delta x^2-\delta y^2 - \delta z^2 = (\delta x^0)^2-(\delta x^1)^2-(\delta x^2)^2-(\delta x^3)^2$
where we have to keep straight that in writing something like $(\delta x^m)^n$, the $m$ is an index and the $n$ is a power.
So the exercise here is to form the invariant $\delta R^2$ using these new 4-vectors, which means we need to have a way to mix $\delta x^\mu$ and $\delta x^\nu$ with a matrix $\eta_{\mu\nu}$ where when we sum over the indices $\mu$ and $\nu$ we get the right answer for the invariant $\delta R^2$:
$\delta R^2 = \sum\limits_{\mu,\nu=0}^3\eta_{\mu\nu}\delta x^\mu\delta x^\nu$ and we sum over the indices $\mu$ and $\nu$, running from 0-3 each.
Equating the two formulae for $\delta R^2$ we can see that $\eta_{00}=+1$, $\eta_{11}=\eta_{22}=\eta_{33}=-1$, and all other components of $\eta$ are identically $0$.
The matrix $\eta $ is called the metric, and we will follow the usual convention where we leave off the $\sum$ symbol if we see the same index as both a subscript and a superscript, and assume the sum is there (in other words, when we write something like $a^\mu b_\mu$, because we see the same index in both we know it really means $\sum\limits_{\mu=0}^3 a^\mu b_\mu$).
Note that it would be perfectly ok to have a relativistic invariant that is negative. That is, to have the invariant be given by $\delta R^2 = -\delta t^2+\delta x^2+\delta y^2 + \delta z^2$ in which case the metric would then have $\eta_{00}=-1$, $\eta_{11}=\eta_{22}=\eta_{33}=+1$, and all other components of $\eta $ identically $0$. The way we've defined it is often referred to as the "West Coast metric" ($+---$), with the "East Coast metric" being ($-+++$). I like the west coast metric since it favors time over distance, and given the large value of the speed of light, that makes sense: $c\delta t$ is pretty much always bigger than $\delta r$. Also it means that in the proper frame, the invariant $\delta R$ is the same as the proper time $\delta \tau $, whereas with the east coast metric, $\delta \tau =-\delta R$. But in the end, either one is ok, and the important thing is to be consistent.
If we want to use real matrix notation, we have to be a bit specific. The vector $x^\mu $ is a regular vector, and has either 4 rows and 1 column (4x1) or 1 row and 4 columns (1x4). Which one? What people usually do is to define the 4-vector $x^\mu $ as a 4x1 object:
$x^\mu = \begin{pmatrix} t \\ x \\ y \\ z\end{pmatrix}$
and write the metric $\eta $ as a 4x4 object: $\eta_{\mu\nu}= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}$
To form an invariant, which is a scalar (a 1x1 object), we need to use the transpose:
$(x^\mu)^T=\begin{pmatrix} \delta t & \delta x & \delta y & \delta z\end{pmatrix}$
so that we get a scalar: (1x1) = (1x4)(4x4)(4x1), or equivalently:
$\delta R^2 = x^T\cdot\eta\cdot x$.
As stated above, some people call $\delta R^2$ the "proper time", and it certainly is true that $\delta R=\delta \tau $ in the "proper frame", but otherwise it's just a semantic convention.
Notice that the metric $\eta _{\mu\nu}$ transforms the vector $x^\mu$ in the following way:
$\eta_{\mu\nu}x^\nu = x_\mu$
so that we can write the invariant as
$\delta R^2 = \delta x_\nu\delta x^\nu$
which means that
$x_\mu\equiv(t,-\vec{x})$
or in matrix form:
$x_\mu = \begin{pmatrix} t & -x & -y & -z\end{pmatrix}$
Remember, to get a scalar invariant, we want to multiply a (1x4) and a (4x1), so $x_\nu$ is a (1x4) and $x^\mu$ is a (4x1).
We can also write the infinitesimal time proper time interval $d\tau $ as
$d\tau = \sqrt{\eta_{\mu\nu}dx^\mu dx^\nu}$.
This will turn out to be a very important formula in GR, but we can get started here just in considering paths in spacetime.
Motion in Space-time
Let's go back to the twin paradox. The path in spacetime for the person stationary on the earth yields a larger time interval (larger proper time in that person's frame) than the path in spacetime of the spaceship (the person on the spaceship ages less). So straight paths (earth) have larger proper time than paths that are not straight (spaceship turns around at the endpoint). Is this a general rule? If it is, then we should be able to form the proper time, apply variational principles, require an extremen, and see what comes out.
It's easier to restrict motion in 1 space dimension, so we start there:
$d\tau = \sqrt{\delta t^2 - \delta x^2}$
and apply the usual machinery to form the extremen in
$\delta\tau(A\to B)=\int_A^B d\tau = \int_A^B\sqrt{dt^2 - dx^2}= \int_{t_A}^{t_B}\sqrt{1-(\frac{dx}{dt})^2}dt$
over some path. The machinery is, of course, the Euler-Lagrange equations:
$\frac{d}{dt}\frac{\partial f(\dot x,x)}{\partial\dot x}-\frac{\partial f(\dot x,x)}{\partial x}=0$
where here, $f(\dot x,x)=\sqrt{1-\dot x^2}$
Since the function has no explicit $x$ dependence, we get the following equation from applying the Euler-Lagrange equations (and below we will use the notation $\beta = \dot x$):
$\frac{\beta}{\sqrt{1-\beta^2}}=$constant.
Recognizing that $\frac{1}{\sqrt{1-\beta^2}}=\gamma$, and multiplying both sides by the rest mass $m$ of the particle we have $m\gamma\beta\equiv p=$constant which is nothing more than momentum conservation.
Lorentz Transformation
The Lorentz transformation (see equations (\ref{eq4})-(\ref{eq6})) can also be written in similar notation like this:
$x^\nu = \Lambda^\nu_\mu x'^\mu$
where the object $\Lambda$ is also a 4x4 matrix given by:
$\Lambda^\nu_\mu = \begin{pmatrix} \gamma & \gamma\beta & 0 & 0 \\ \gamma\beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$
Note that the Lorentz matrix has both an upper and lower index, and is a symmetric matrix so that in matrix notation $\Lambda = \Lambda^T$.
In matrix form, we would have $x=\Lambda\cdot x'$ where the vectors $x$ and $x'$ are column vectors (a 4x1 object) and $\Lambda$ is of course 4x4. If we want to apply the Lorentz transformation to a row vector (1x4 object), then the equation has to be $x^T=(x')^T\Lambda ^T=(x')^T\Lambda$.
We can form the Lorentz invariance and compare it in the two frames $O$ and $O'$ (leaving the transpose of $\Lambda$ in there just to be explicit) to get:
$x^T\eta x$=(x')^T\Lambda^T\eta\Lambda x'=(x')^Tx'$, which means that
$\Lambda^T\eta\Lambda = \eta$.
What does this mean? Best to look at it as 3 matrices, and remember that $\Lambda$ is a symmetric matrix ($\Lambda=\Lambda^T$):
$\Lambda^T\eta\Lambda = \begin{pmatrix} \gamma & \gamma\beta & 0 & 0 \\ \gamma\beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} \gamma & \gamma\beta & 0 & 0 \\ \gamma\beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} \gamma & \gamma\beta & 0 & 0 \\ \gamma\beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \gamma & \gamma\beta & 0 & 0 \\ -\gamma\beta & -\gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}$
as it should (making use of the definition of $\gamma$ which can be written as $\gamma^2 -\gamma^2\beta^2 = 1$.
What is really interesting here, among other things, is the significance of 4-vectors that have upper indices (a "contravariant" vector) and those that have lower indices (a "covariant" vector). And, on top of that, the correspondence between the 4-vector notation here (e.g. $x^\mu $ is a "thing" in Minkowski space) and the matrix notation where we suppress the indices, but have to keep track of rows and columns and use the transpose "T" concept. For instance, to form a scalar with the two Minkowski 4-vectors $a^\mu $ and $b^\mu $, both contravariant vectors, we have to first lower one of them to make a covariant object, e.g. $a_\mu =\eta _{\mu\nu}a^\nu $ to form the scalar object $a_\mu b^\mu $. In matrix notation, to make a scalar from a 4-vector, we need to multiply a 1x4 object on the left by a 4x1 object on the right. Note that the matrix representation of the vector $x$ is that it is a contravariant thing, because we defined it such that to get the covariant $a_\mu$ we contract it on with $\eta_{\mu\nu}$ on its left, equivalent to multiplying a 4x4 object by a 4x1 object (in that order). So 4x1 column vectors are contravariant, and 1x4 row vectors are covariant, and the relationship between a 1x4 and a 4x1 is that they are transposes of each other. In Minkowski space the metric rotates from one to the other, so in matrix space the metric is intimately tied up with making the transpose.
Why is this the case? Ultimately it boils down to the metric being needed to form a scalar in the first place, or in other words, the fact that the metric is not equal to the unit matrix (all 1's on the diagonal and 0's everywhere else).
More on Metrics
The metric $\eta_{\mu\nu}$ is a symmetric matrix with constant values. But this entirely tied to the choice of using Cartesian coordinates. To see this, imagine that we were to use spherical coordinates $r,\theta,\phi$ instead of $x,y,z$. We would need to calculate the relativistic invariant $\delta R^2=\delta t^2 - \delta x^2 - \delta y^2 - \delta z^2$ in terms of the intervals $\delta t$, $\delta r$, $\delta\theta$, and $\delta \phi$. This is pretty straight forward: start with the definitions of $r,\theta,\phi$:
$x = r\sin\theta\cos\phi$
$y = r\sin\theta\sin\phi$
$z = r\cos\theta$
Then calculate
$dx = dr\cdot\sin\theta\cos\phi + d\theta\cdot r\cos\theta\cos\phi -
d\phi\cdot r\sin\theta\sin\phi$
$dy = dr\cdot\sin\theta\sin\phi + d\theta\cdot r\cos\theta\sin\phi +
d\phi\cdot r\sin\theta\cos\phi$
$dz = dr\cdot\cos\theta - d\theta\cdot r\sin\theta$
When we form the invariant with these substitutions, we get the following for the differential form of the invariant:
$dR^2 = dt^2 - dr^2 - r^2d\theta^2 - r^2\sin^2\theta d\phi^2$
If we then form the metric $g_{\mu\nu}$ such that $dR^2=g_{\mu\nu}dX^\mu dX^\nu$ where $X^\mu =(t,r,\theta,\phi)$ we would see that $g_{\mu\nu}$ is also a symmetric 4x4 matrix with diagonal elements $g_{00}=1$, $g_{11}=-1$, $g_{22}=-r^2$, and $g_{33}=-r^2sin^2\theta$, and the proper time would be given by $d\tau = \sqrt{R^2}=\sqrt{g_{\mu\nu}(X)dX^\mu dX^\nu}$.
As above, the motion would be given by applying the Euler-Lagrange equations to what's inside the square root. If we pull out the local time derivative $dt$ from the above equation, we would again have the path given by
$\frac{d}{dt}\frac{\partial f(\dot x,x)}{\partial\dot x}-\frac{\partial f(\dot x,x)}{\partial x}=0$
where $f(\dot x,x)=\sqrt{g_{\mu\nu}(X)dX^\mu dX^\nu}$.
Gravity, General Relativity, and Geodesics
When first articulated, Newton's laws of gravity were a revelation. Newton was particulary concerned with using mathematics and observation to understand nature, and reconciling the two via theoretical considerations were mostly what he was interested in (he was an incurable mystic, but that's another story). Newton was not particuarly concerned with issues of "action at a distance", something that became an immediate issue with his theory of universal gravitation.
To make a long story short, Einstein extended the "special" relativity (special in that he dealt with the case of constant velocities) into a more general theory that could incorporate accelerations in a 4-dimensional space-time, and found a very interesting thing: that accelerated motion produced the same effects as did gravity. Or in other words, you can't tell the difference, which means they are the same, and this is what the famous "Principle of Equivalence" is all about (see the Wikipedia article, it's not bad!).
The idea is simple: motion is in 4 dimensions, and is determined by the geometry (curvature) of the 4-dimensional space. And the curvature, or deviation from "flat", is from mass. Or as is often stated rather tersely, mass tells space-time how to curve, and curved space-time tells mass and energy how to move.
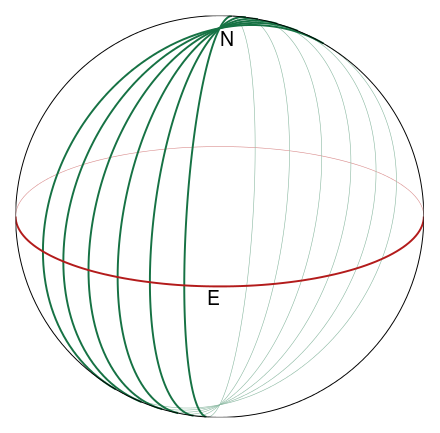
As seen above, straight-line motion (constant velocity) maximizes the proper time (see this section). One can show mathematically that any motion in a curved space is along a path called a "geodesic" that in 4-space maximizes the proper time. It's sometimes easier to think in 3 dimensions than 4: imagine we have a sphere, and motion is restricted to the surface. The motion then would be in a curved space. The following figure shows the motion you would get if you threw a projectile in a straight line, constrained to the 2-dimensional surface:

The General Theory of Relativity reconciles gravity with motion in a 4-dimensional space-time. We now know that such motion is along a geodesic, which maximizes the proper time, which you can write like this:
$d\tau = \frac{dt}{\gamma}\label{dproptime}$
We can expand this out using equation (\ref{eq7p}) to get
$d\tau = dt\sqrt{1-\beta^2} = dt\sqrt{1-(\frac{dx}{dt})^2-(\frac{dy}{dt})^2-(\frac{dz}{dt})^2} =\sqrt{dt^2-dx^2-dy^2-dz^2}=\sqrt{g_{\mu\nu}x^\mu x^\nu}$
So apparently, $g_{\mu\nu}$ is telling you how things move. It is also telling you about the curvature! In special relativity, $g_{\mu\nu}=\eta_{\mu\nu}$ (flat space-time)$ but in general, $g_{\mu\nu}$ can have curvature.
Here is where Einstein applies his theory of gravity as being equivalent to motion along geodesics in any kind of curved 4-d space-time. Which means that in order to understand the motion, we need an equation for how to calculate the curvature, which is incorporated into $g_{\mu\nu}$. His equations must reflect the idea that mass (and energy) warp space-time, so it should have in it a term that deals with how the space is curved, a term that describes the mass-energy, and the metric $g_{\mu\nu}$. The equation he came up with is the following: $$G_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}$$ where $$G_{\mu\nu}\equiv R_{\mu\nu}-\half Rg_{\mu\nu}$$ and $$R\equiv g^{\mu\nu}R_{\mu\nu}$$ $R_{\mu\nu}$ is called the "Ricci tensor" and is related to the curvature, and along with $g_{\mu\nu}$ how motion will be carried out locally. $T_{\mu\nu}$ is the energy-momentum tensor, $G$ is the gravitation constant ala Newton ($6.67\times 10^{-11}$Nm2/kg2), and of course $c$ is the speed of light. These are field equations. All you have to do now is find solutions to the field equations that correspond to the various scenariors (flat spacetime, black holes, etc) and that allows you to find $G_{\mu\nu}$ and therefore how things move.
It is, of course, a bit more complicated than just that, but this is the general idea.