When my kids were little, I'd tell them about gravity and how the force between two bodies was attractive. Then we'd look up at the moon and I'd ask "what keeps it up there"? Their conclusion was that gravity must not be what I said it was!
The motion of bodies under the influence of gravity are called orbits, and the dynamics of such motion is indeed interesting and complex. The lesson here is that as is much of physics, motion can sometimes be counter-intuitive. So, what is the core concept that allows us to understand how the moon stays up there? Best to start at the beginning, which means consider the forces at work, in this case gravity.
The beginning starts with Newton's Law of Universal Gravitation, which says the following:

By Newton's laws, the gravitational force is given by: $$\vec{F} = \frac{Gm_1m_2}{r^2}\hat{r}\label{edm1m2}$$ Given that the force is along the direction between them, we can say that the motion will have an acceleration only along that direction, and not along any other orthogonal direction. According to Newton's 1st law of motion, a body in motion will stay in motion unless acted upon by a force. That means that if there is any motion in the direction orthogonal to the radial direction, then that motion will be characterized by a constant velocity along that direction. This is actually the origin of conservation of angular momentum (more on that below), which will always occur whenever the forces are "central", as is the case for gravity (and the Coulomb force as well).
For central $1/r^2$ forces such as gravity, we can solve for the two-body motion analytically. As we will see below, the motion depends on the total energy of the system, and the interplay between the kinetic and potential energy:
This chapter mostly discusses bound state orbits ($E\lt 0$), which are generally elliptical. So to begin, we first discuss the mathematics of ellipses, just to have it ready when we apply it to the physics.
The Ellipse | Back to top |
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\label{eellxy}$$
The range of $x$ is $\pm a$ and $y$ is $\pm b$, and let's say $a>b$. The figure looks like this:
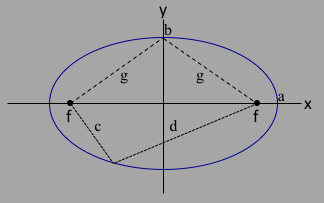
The quantity $f$ is called the focus, and the ellipse is defined such that if you calculate the distance of any point on the ellipse to the two foci and add together, you get a constant value no matter what point you use. So the distance $2g$ is equal to the distance $c+d$, which is also equal to the distance from each focus to the point $[x,y]=[a,0]$ given by $2a$. So we have our first formula:
$g=a$
Since $a>b$, $x$ is called the major axis and $y$ the minor axis, and the quantity $a$ and $b$ are often called the "semi-major" and "semi-minor" axis lengths.
Since the two focal points are equidistant from the origin, then we can calculate the hypotenuse using $g^2 = f^2 + b^2$, and substituting for $g=a$ we have
$a^2 = b^2 + f^2$
The ratio between the focal point and the semi-major axis length, $f/a$ is called the "eccentricity".
$$e \equiv f/a$$
Combining these equations gives
$b^2 = a^2 - f^2 = a^2(1-(f/a)^2) = a^2(1-e^2)$
which gives the other useful equation
$$(b/a)^2 = 1-e^2\label{eeba}$$
A circle would be the special case of an ellipse with $b=a$, which implies $e=0$, so we can say that $e$, the eccentricity, measures the deviation from a circle ($e=0$ means a circle).
In the figure below, you can drag around the black circles at the endpoints of the $x$ and $y$ axes, and see how the eccentricity and foci change. (The program will not let you make the semi-major axis swap from $x$ to $y$ however.)
e=
| |
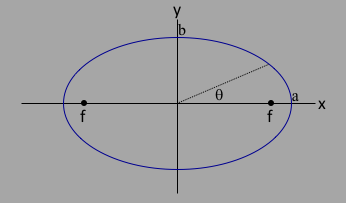
To see the equation for the ellipse in polar coordinates, we transform from $[x,y]$ to $[r,\theta]$ ($\theta$ measures the angle between the line from the origin to the point on the ellipse with the major axis as in figure 2) using: $$x = r\cos{\theta}\label{eqx}$$ $$y = r\sin{\theta}\label{eqy}$$ And plug into equation $\ref{eellxy}$ to get:
$r^2(b^2\cos^2\theta + a^2\sin^2\theta) = a^2b^2$, which after some algebra gives
| $r$ | $=$ | $\frac{b}{\sqrt{1-e^2\cos^2\theta}}$ |
| $=$ | $a\sqrt{\frac{1-e^2}{1-e^2\cos^2\theta}}\label{eellrt00}$ |
where here the origin is between the two foci and $\theta$ is the angle between any origin-ellipse point and the major axis as in figure 1 above.
This equation makes is clear that the condition $e=0$ means $r=b$, a constant, and thus a circle.
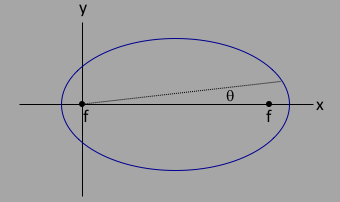
In discussing orbital mechanics, it is useful to have the equation for an ellipse centered at one of the foci. To do this, we would only have to take equation \ref{eellxy} and translate by $x\to x-f$. After some algebra, we would get the equation: $$r = \frac{a(1-e^2)}{1\pm e\cos\theta}\label{eellrtf}$$ where now $\theta$ is the angle between the major axis and a point on the ellipse relative to one of the foci as in figure 3 below. The $\pm$ sign mean tells you which foci is at the origin: "$+$" means that $r$ is minimal at $\theta=0$, so the origin coincides with the focus on the right, and "$-$" sign in the denominator means that the origin coincides with the focus on the left. The figure below would correspond to having $1-e\cos\theta$ in the denominator for equation $\ref{eellrtf}$, where the origin coincides with the focus on the left.
| Equation of ellipse centered at origin | $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ | |
| Equation of ellipse centered at focus $f$ | $\frac{(x-f)^2}{a^2} + \frac{y^2}{b^2} = 1$ | |
| Definition of focal point | $f^2 = a^2 - b^2$ | |
| Definition of eccentricity | $e=f/a$ | |
| $a$, $b$, and $e$ | $(b/a)^2 = 1-e^2$ | |
| $r(\theta)$ for ellipse centered at origin | $r = \frac{b}{\sqrt{1-e^2\cos^2\theta}}=a\sqrt{\frac{1-e^2}{1-e^2\cos^2\theta}}$ | |
| $r(\theta)$ for ellipse centered at focal point | $r = \frac{a(1-e^2)}{1\pm e\cos\theta}$ | |
| $r_a$ (apicenter) and $r_p$ (pericenter) | $r_a = a(1+e)$ and $r_p = a(1-e)$ |
An Introduction to Orbits | Back to top |
Newton's law of universal gravitation, an inverse square law, holds here, so the equations of motion will be goverened by the 3 forces:
| $\vec{F_r} = -\hat{r}GM_em/r^2$ |
| $\vec{F_\theta} = 0$ |
| $\vec{F_z} = 0$ |
If the satellite starts with some non-zero tangential velocity $\vec{v_t}$ as an initial condition, then since the force is along the radial direction, and we would expect that any motion would be confined to a plane defined by the radial vector $\vec{r}$ and the inital velocity $\vec{v_t}$. So we can make things easier and have the initial velocity vector $\vec{v_t}$ point along the $\hat\theta$ direction, so that $v_t=v_\theta$, and the satellite will be confined to the $xy$ (or equivalently, $r\theta$) plane.
Starting with no initial velocity, the satellite will fall. If you start with a nonzero velocity in the $\hat\theta$ direction, the satellite will also fall, but it will also move along the azimuthal direciton. For small values of $v_\theta$, the satellite hits the surface of the earth. As you increase $v_\theta$, you can see the arc of the path hit the earth at a location that gets closer to the opposite side as $v_\theta$ increases. At some point ($v_\theta = 4.8$ here, however this is arbitrary and only depends on the scale of the variables used in the simulation code), you can see a full orbit. By definition, the positions of furthest and closest approach of orbits in general are called the apocenter and pericenter points respectively (they are also sometimes refered to as apoapsis and periapsis). If the situation is with a satellite orbiting the earth, these positions are called the apogee and perigee, and if it's an orbit around the sun, aphehelion and perihelion. In the simulation, for sufficiently large $v_\theta$, you see the full orbit starting at apogee and grazing the surface at perigee. Note how the velocity varies around the orbit - it is greatest at perigee and smallest at apogee. This is nothing more than conservation of energy $E=T+V$: $V$ is largest at apogee when the satellite is furthest away, so $T$ will be smallest there. And vice versa at perigee.
As you increase $v_\theta$ even more than the minimum needed for an orbit, you get to a point where the eccentricity approaches 1, $v_p\!=\!v_a$, $r_p\!=\!r_a$, $e\!=0$, and the orbit is circular. Increasing still further, the apicenter and pericenter switches, the initial conditions describe the pericenter, and the motion is still elliptical. You can see this clearly from equation $\ref{eevavp}$ below. At this point, we have the condition $\half v_p^2=g/r_p$, which from the equation $\ref{eapper}$ gives $\varepsilon=0$. The motion is parabolic, which can be seen by using equation $\ref{eellrtf}$, setting $e\!=\!1$, and substituting $r^2=x^2+y^2$ and $x=r\cos\theta$. As $v_p$ increases even more, the motion becomes hyperbolic, and the satellite is no longer bound.
In the canvas below, you can see the image of the Earth, and a green satellite at some initial distance. By using the slider, you can change the initial tangential velocity ($v_\theta$), rerun the simulation, and see how things change. There is a table where we show the apogee $r_{apo}$, the perigee $r_{per}$, and the velocity at perigee $v_{per}$. We also show the semi-major and semi-minor axis lengths $a$ and $b$, the eccentricity $e$, the focal point distance $f$ (the simulation places a small black circle at those focal points), and the value for the inital velocity at apogee that allows for a full orbit $v_{orb}$ (the condition for this is that $r_{per}\ge R_{earth}$). Note that $a$, $b$, and $f$ are all relative to the center of the ellipse, which is halfway between the two focal points.
So this is basically what I tried to tell my kids: the moon does fall, but it also moves out of the way and so never hits the earth. Interestingly, neither went into physics or astronomy!
The next chapter discusses the equations of motion, and quantifies things.
| Initial transverse velocity $v_\theta$: | ||
| Scale by: |
| $r_{apo}$ | $v_{apo}$ | $r_{per}$ | $v_{per}$ | $e$ | $a$ | $b$ | $f$ | $v_{orb}$ |
250
|
Orbital Mechanics | Back to top |
$$\vec{F}\!(r) = \frac{-GMm}{r^2}\hat{r}\label{eqgforce}$$
and the potential will be
$$V(r)=\frac{-GMm}{r}\label{eqpotential}$$
Since the force is radial, the plane of the motion will be constant, which means we can restrict the motion to the $r\theta$ coordinates (radial and azimulth directions) and ignore the $z$ component.
Using $|\vec{\dot{r}}\!|^2 = \dot{x}^2 + \dot{y}^2$, the kinetic energy $T$ is given by
$$T\label{eqkinetic}=\half m|\vec{\dot{r}}\!|^2=\half m(\dot{x}^2 + \dot{y}^2)$$
We switch to polar coordinates using equations $\ref{eqx}$ and $\ref{eqy}$ and calculate the time derivatives to be:
$\dot{x}=\dot{r}\cos{\theta} - r\dot{\theta}\sin{\theta}$
$\dot{y}=\dot{r}\sin{\theta} + r\dot{\theta}\cos{\theta}$
This gives the following after substitution:
$$v^2 = \dot{x}^2 + \dot{y}^2 = \dot{r}^2 + r^2\dot{\theta}^2$$ Now we can form the Lagrangian and crank through the equations of motion. What we are after is an understanding of the dynamics, which starts with an understanding of what the various elliptical parameters $e,a,b,f$ depend on. For the full treatment, see below.
For a quicker way, we first start with an ellipse centered at the left foci as in figure 3 and use equation $\ref{eellrtf}$ (reproduced below) for the motion as a function of $\theta$ and the eccentricity $e$: $$r = \frac{a(1-e^2)}{1 + e\cos\theta}$$ We can differentiate to get
| $\dot r$ | $=$ | $\frac{ae(1-e^2)\dot\theta\sin\theta}{(1+e\cos\theta)^2} $ |
| $=$ | $\frac{er^2\dot\theta\sin\theta}{a(1-e^2)}$ | |
| $=$ | $\frac{e\ell\sin\theta}{a(1-e^2)}$ |
The important thing to notice here is that $\dot r$ only depends on $\theta$ ($\ell,a,e$ are all constant), which means $\dot r=0$ at $\theta=0,\pi$, which means the radial velocity vanishes at apicenter and pericenter.
Next, using the above equations $\ref{eqpotential}$ and $\ref{eqkinetic}$ and going to polar coordinates, we form the total energy $E$
| $E$ | $=$ | $T+V$ |
| $=$ | $\half m|\vec{\dot{r}}\!|^2 - \frac{GMm}{r}$ | |
| $=$ | $\half m(\dot{r}^2 + r^2\dot\theta^2) - \frac{GMm}{r}\label{elagrange}$ |
At apicenter and pericenter, knowing that $\dot r_a=\dot r_p=0$, we have $$\varepsilon = \frac{\ell^2}{2r^2} - \frac{g}{r}\label{eapper}$$ Rearranging to get a quadratic in $r$ gives $$2\varepsilon r^2 + 2gr - \ell^2 = 0\label{erel}$$ Solving for $r$ gives $$r = \frac{-g\pm\sqrt{g^2 + 2\ell^2\varepsilon}}{2\varepsilon}$$ Remembering that $\varepsilon\lt0$ for bound orbits, we can write $\varepsilon = -|\varepsilon|$ to get $$r = \frac{g\pm\sqrt{g^2 - 2\ell^2|\varepsilon|}}{2|\varepsilon|}\label{ere}$$
The $\pm$ sign tells you the difference between $r_a$ and $r_b$: $$r_a = \frac{g + \sqrt{g^2 - 2\ell^2|\varepsilon|}}{2|\varepsilon|}$$ $$r_p = \frac{g - \sqrt{g^2 - 2\ell^2|\varepsilon|}}{2|\varepsilon|}$$
Going back to equation $\ref{ere}$, if you remember that $2a=r_a+r_p$ you can easily write down that $2a = -g/\varepsilon$, or $$\varepsilon = -\frac{g}{2a}$$ This is a great equation - it says that for central force gravitational forces, knowing the energy of the satellite will determine the length of the major axis. Does it also tell you all you need to know the eccentricity? To answer this, go back to equation $\ref{erel}$ and substitute for $r$ using either $r_a = a(1+e) = -g(1+e)/2\varepsilon$ or the similar equation for $r_p$, and crank through. After a few lines of algebraic simplification, you should get the equation $$e = \sqrt{1+\frac{2\varepsilon\ell^2}{g^2}}\label{eeeLE}$$ From equation $\ref{eellxy}$, we see that we need 2 parameters to describe the ellipse: $a$ and $b$. So it should be no surprise that we need to know 2 constants of the motion: $\varepsilon$ and $\ell$. (And of course we can use equation $\ref{eeba}$ to find the eccentricity $e$ knowing $a$ and $b$.)
To complete the equations of motion, we can take equation $\ref{eeeLE}$ and substitute
$\varepsilon = -\frac{g}{2a}$ to get
$$\ell^2 = ag(1-e^2)\label{eell}$$
Now that we have $a(1-e^2)=\ell^2/g$ and $e$ as in equation $\ref{eeeLE}$, we can use
equation $\ref{eellrtf}$ to get the equation of
motion for a satellite relative to the origin at the foci:
$$r = \frac{\ell^2/g}{1- \sqrt{1+\frac{2\varepsilon\ell^2}{g^2}}\cos\theta}$$
We can also use $\ref{eell}$ to tell us something about the velocities at apicenter
and pericenter, $v_a$ and $v_p$.
Since the angular momentum is conserved, we would have that
$\ell = r_av_a = r_bv_b$. Plugging this into equation $\ref{eell}$ and using
$r_a=a(1+e)$ and $r_b=a(1-e)$, we can get
$$v_a = \sqrt{\frac{g}{a}\frac{1-e}{1+e}}$$
$$v_p = \sqrt{\frac{g}{a}\frac{1+e}{1-e}}$$
$$v_p = v_a\frac{1+e}{1-e}$$
Or, if we substitute $r_a=a(1+e)$ and $r_p=a(1-e)$, we get the following nice equations:
$$e = 1 - \frac{r_av_a^2}{g} = \frac{r_pv_p^2}{g} - 1\label{eevavp}$$
Everything is therefore determined once you have the initial conditions, either in the
form of $r_a,v_a$ (remember that $r_av_a=r_pv_p$) or $\varepsilon,\ell$.
Useful formulae...
Definition:
$g\equiv GM$
Constants of the motion $\varepsilon$ and $\ell$ at apicenter/paricenter
$\varepsilon = \half v_a^2 - g/r_a$ and $\ell = v_ar_a$ (or substitute $a\to p$)
Semi-major axis and eccentricity
$a = -g/\varepsilon$ and $e = \sqrt{1-\ell^2/g}$
position of apicenter
$r_a = a(1+e) = \frac{g + \sqrt{g^2 - 2\ell^2|\varepsilon|}}{2|\varepsilon|}$
position of pericenter
$r_p = a(1-e)=\frac{g - \sqrt{g^2 - 2\ell^2|\varepsilon|}}{2|\varepsilon|}$
$r(\theta)$ and initial conditions for energy ($\varepsilon$) and angular momentum ($\ell$)
$r = \frac{\ell^2/g}{1- \sqrt{1+\frac{2\varepsilon\ell^2}{g^2}}\cos\theta}$
Eccentricity as a function of apicenter and pericenter initial $r$ and $v$
$v_a = \sqrt{\frac{g}{a}\frac{1-e}{1+e}}$ $v_p = \sqrt{\frac{g}{a}\frac{1+e}{1-e}}$
$v_p = v_a\frac{1+e}{1-e}$
Lagrangian Formulation | Back to top |
$$L=\half m(\dot{r}^2 + r^2\dot{\theta}^2) + \frac{GMm}{r}\label{elagrange1}$$ Using the Euler-Lagrange equations we have the following equation for the components $r$: $$\frac{d}{dt}m\dot{r} - mr\dot{\theta}^2 + \frac{GMm}{r^2}$$ and $\theta$: $$\frac{d}{dt}mr^2\dot{\theta}=0\label{eLcons}$$ The last equation says that the quantity $mr^2\dot{\theta}$ is constant, and indeed this is the angular momentum ($\vec{L}=\vec{r} \times \vec{p}$) for motion in a plane: $$L\equiv mr^2\dot{\theta}\label{eL}$$ Using this we can subsitute into the radial equation to get: $$\ddot{r} - \frac{L^2}{mr^3} + \frac{GM}{r^2}=0\label{eLr}$$
Conservation of angular momentum played a big role in connecting Newton's laws of motion to Kepler's. Here, the motion in a plane looks like the following figure:
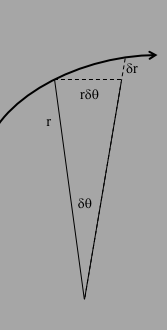
$\delta A = \half r\cdot r\delta\theta + \half \delta r\cdot r\delta\theta$ + higher order...
The 2nd term is 2nd order in the differentials, so we can drop that when we take the limit as $\delta\theta \to 0$, leaving
$\delta A = \half r\cdot r\delta\theta$
which means that
$\frac{\delta A}{\delta t} = \half r^2\frac{\delta\theta}{\delta t}$
or equivalently:
$\dot A = \half r^2\dot{\theta}^2\label{eAdot}$
If we multiply equation $\ref{eLcons}$ by $1/2m$, we would get
$\frac{d}{dt}\half r^2\dot{\theta}=0$
which means that $\dot A$ is conserved, which means that $\delta A = k\delta t$, where $k$ is some constant, which means that a body sweeps out equal areas in equal times, aka Kepler's 2nd Law.
We can use the Lagrange equations to find $x(t)$ and $y(t)$, but it is usaully more useful to find an equation for the "orbit", or in other words how the radius depends on angle: $r(\theta)$. To accomplish this, we will need to solve equation $\ref{eLr}$.
To do this, we use the chain rule:
$\frac{d}{dt} = \frac{d\theta}{dt}\frac{d}{d\theta}=\dot\theta\frac{d}{d\theta}$
Then, going back to equation $\ref{eL}$, we can substitute for $\dot\theta$ to get
$\frac{d}{dt} = \frac{L}{mr^2}\frac{d}{d\theta}$
We can then apply this to simplify:
$\ddot{r} = \frac{d}{dt}\frac{d}{dt}r = \frac{L}{mr^2}\frac{d}{d\theta}\frac{L}{mr^2}\frac{d}{d\theta}r$
This doesn't look like a simplification, until you make the following substitution: $$u\equiv 1/r\label{eur}$$ Then $\ddot r$ becomes
$-\frac{L^2}{m^2}u^2\frac{d^2u}{d\theta^2}$ and equation $\ref{eLr}$ becomes
$-\frac{L^2}{m^2}u^2\frac{d^2u}{d\theta^2} - \frac{L^2}{m^2}u^3 + GMu^2 = 0$
Multiplying each term by $m^2/(L^2u^2)$ and rearranging gives
$u'' + u = \frac{GMm^2}{L^2}$
where $u''$ means $d^2u/d\theta^2$. As we did above, we can collect symbols by defining $g\equiv GM$ and $\ell=L/m$ to give $$u'' + u = g/\ell^2$$ This equation is clearly sinosoidal, with solution
$u(\theta) = g/\ell^2 + B\cos(\theta - \theta_0)$ or going back to $r(\theta)$:
$$r(\theta) = \frac{1}{g/\ell^2 \pm B\cos(\theta - \theta_0)}\label{ertheta}$$
where $B$ and $\theta_0$ are initial conditions.
For the initial condition $\theta_0$, let's set $\theta_0=0$, which is pretty innocuous as a starting angle (see figure 2), and lets also set the origin at the left foci as in figure 3, which resolves the $\pm$ ambiguity in favor of $-$ (so that $r$ is a maximum at $r_0$). We then would have $r_0$, $v_0$, and $E_0$ evaluated at the same point (more on this later, see figure 4 below).
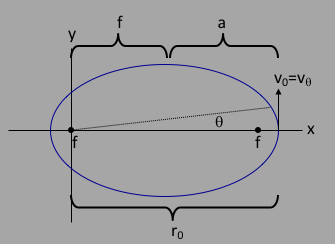
To solve for $B$, we can use the initial condition
$1/r_0 \equiv 1/r(0) = g/\ell^2 + B$
and go back to the other constant of the motion, the energy $E$, which is the sum $T+V$ and is given by
| $E$ | $=$ | $T+V$ |
| $=$ | $\half m(\dot{r}^2 + r^2\dot{\theta}^2) - \frac{GMm}{r}$ |
Since $E$ is constant, we can evaluate it anywhere, and the convenient place would be where $\dot{r}=0$. If you take the derivative of equation \ref{ertheta} and set it to 0, you will find that $\dot r=0$ happens when $\theta = 0$, and at that point $r=r_0$, which allows you to write
$$\varepsilon = \half r_0\frac{\ell^2}{r_0^4} - \frac{g}{r_0} = \frac{\ell^2}{2r_0^2} - \frac{g}{r_0}$$
Here is the trick: replace $1/r_0$ in the above equation for the energy with $B + g/\ell^2$, and solve for B. You should get
$$B = \frac{g}{\ell^2}\sqrt{ 1+\frac{2\varepsilon \ell^2}{g^2} }$$
Substituting that back into equation $\ref{ertheta}$ and rearranging gives:
$$r(\theta) = \frac{\ell^2/g}{ 1-\sqrt{ 1+\frac{2\varepsilon \ell^2}{g^2} }cos\theta }\label{eellipser}$$
This equation is clearly that of an ellipse: $-1\lt\cos\theta\lt +1$, therefore $(g/\ell^2+B)\lt\!1/r\lt(g/\ell^2-B)$, and $r$ is the same for $\theta = 90$ and $270$ degrees.
Equating equations $\ref{eellrtf}$ and $\ref{eellipser}$ allows you to solve for the eccentricity in terms of the initial conditions, giving $$e = \sqrt{ 1+\frac{2\varepsilon \ell^2}{g^2}}\label{eee}$$ (Remember that $\varepsilon\lt 0$ is constant as is $\ell\equiv L/m$.) Note that here, the eccentricity $e$ will also be given by the ratio of the distance between the two foci $f$ and the length of the major axis (the distance between there the ellipse intersects the $x$ axis).
Also by equating equations $\ref{eellrtf}$ and $\ref{eellipser}$, we can solve for the semi-major axis length $a$ to get a very interesting result: $$a = -\frac{g}{2\varepsilon}$$
This equation also says that $\varepsilon=-g/2a$, and of course $\varepsilon$ is a constant of the motion. To understand this better, let's first consider a circular orbit where $r$ and $v=r\dot\theta$ are both constants. The kinetic energy will be given by $T=\half mv^2$, and the potential by $V=-GMm/r$ so that total energy will be given by $E = \half mv^2 - GMm/r$. If we consider the centripetal acceleration, held into a circular orbit by a central gravitational force, we can write that
$\frac{mv^2}{r}=\frac{GMm}{r^2}$
or equivalently
$mv^2=\frac{GMm}{r}$
Substituting that into the above equation for $T$ gives $T=\half GMm/r$, or $T=-\half V$. This is called the "virial theorem" as applied to circular orbits. Plugging this new value for the kinetic energy into the equation for the energy gives:
$E = \half \frac{GMm}{r} - \frac{GMm}{r} = -\half\frac{GMm}{r}$
or equivalently
$\varepsilon = -\frac{g}{2r}$
for circular orbits, where here $r$ is the constant radius.
Same formula as for an elliptical orbit, except we use $a$ as the semi-major axis and write
Substituting $\varepsilon=-\frac{g}{2a}$ into equation $\ref{eee}$ gives $$e = \sqrt{ 1-\frac{l^2}{ga}}\label{eea}$$
Note that here we can see explicitly that $e\lt1$ for an ellipse.
This equation is interesting, but not as useful as equation $\ref{eee}$ when it comes to actually doing a calculation and simulation.
Real Two-body Dynamics | Back to top |
The figure below sets up the generalized coordinate system, where $\vec{R_1}$ and $\vec{R_2}$ are the position vectors pointing to the centers of masses $m_1$ and $m_2$.
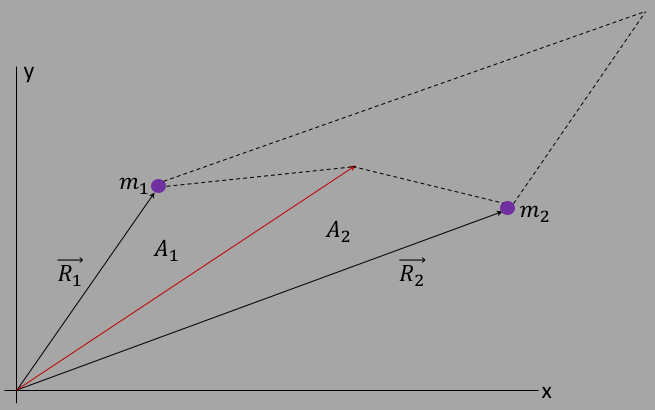
| $S_2$ | $=$ | $\half |\vec{R_1}\times(\alpha\vec{R_1}+(1-\alpha)\vec{R_2})| + $ |
| $\half |\vec{R_2}\times(\alpha\vec{R_1}+(1-\alpha)\vec{R_2})|$ |
where here $\alpha\equiv m_1/(m_1+m_2)$. The terms $\vec{R_1}\times\vec{R_1}$ and $\vec{R_2}\times\vec{R_2}$ vanish, leaving:
| $S_2$ | $=$ | $\half |\vec{R_1}\times(1-\alpha)\vec{R_2}| + \half |\vec{R_2}\times\alpha\vec{R_1}|$ |
| $=$ | $\half |\vec{R_1}\times \vec{R_2}|$ | |
| $=$ | $\half S_1$ |
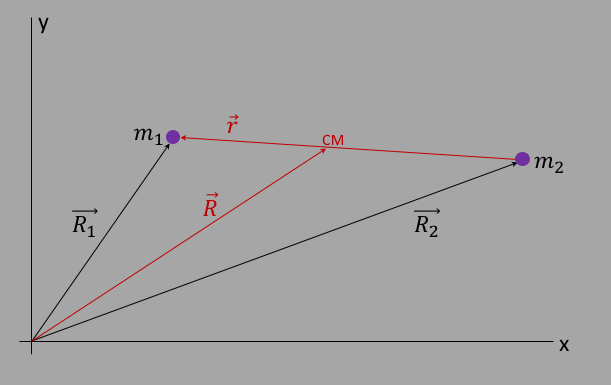
The only way that this can be true is if $\vec{R}$ ends at the connection between the two masses: QED.
We can now change from $\vec{R_1}$ and $\vec{R_2}$ to $\vec{R}$ and $\vec{r}$ in the kinetic and potential energies above to form the Lagrangian. The kinetic energy term becomes
| $T$ | $=$ | $\half m_1 |\vec{\dot r_1}|^2 + \half m_2 |\vec{\dot r_2}|^2$ |
| $=$ | $\half m_1 | \vec{\dot{R}} + \frac{m_2}{M}\vec{\dot{r}}\!|^2 + \half m_2 | \vec{\dot{R}} - \frac{m_1}{M}\vec{\dot{r}}\!|^2$ | |
| $=$ | $\half M|\vec{\dot{R}}\!|^2 + \half\mu |\vec{\dot{r}}\!|^2$ |
where $M\equiv m_1+m_2$ and $\mu \equiv \frac{m_1m_2}{M}$.
The potential energy term will be
$$V = \frac{-Gm_1m_2}{|\vec{r}\!|}$$
so that the full Lagrangian is: $$L = \half M|\vec{\dot{R}}|^2 + \half\mu |\vec{\dot{r}}\!|^2 + \frac{GM\mu}{|\vec{r}\!|}$$ where we have used $M\mu = m_1m_2$.
What's going on here is clear: the vector $\vec R$ represents the center of mass, and $\vec r$ the relative position between the two masses, and so it's clear that 2 body motion can be described by the motion of the center of mass (CM) with total mass $M$ and position $\vec R$, and the motion within the center of mass with the mass $\mu$ and position $\vec r$.
In this case, let's assume that the CM is not changing (there are no forces on the system from outside). The motion is entirely internal and our final Lagrangian will be $$L = \half \mu |\vec{\dot{r}}\!|^2 + \frac{GM\mu}{|\vec{r}\!|}\label{elagrangeCM}$$ This reduces the problem of trying to find the motion of the 2 satellites to the motion of a single satellite around an infinitely larger satellite, given by equation $\ref{eellipser}$, and make the substitution $M\to m_1+m_2$ and $m\to\mu$. Once we have $r(\theta)$, we can use equations $\ref{er1cm}$ and $\ref{er2cm}$, set $\vec{R}=0$ (accomplished via initial conditions, see below), and get $$R_1(\theta)=\frac{\mu}{m_1}r(\theta)$$ $$R_2(\theta)=-\frac{\mu}{m_2}r(\theta)$$ In the first part of this chapter, we used the relative vector $\vec{r} =\vec{R_1}-\vec{R_2}$ because the potential goes like $1/|\vec{r}\!|$. However for the rest of this chapter, we are considering the dynamics of the satellites relative to the CM frame, and it's more convenient to define yet another set of vectors, $\vec{r_1}$ and $\vec{r_2}$, defined as directions relative to the CM position and shown in figure figure 6: $$\vec{R_1}=\vec{R}+\vec{r_1}\label{er1cm2}$$ $$\vec{R_2}=\vec{R}+\vec{r_2}\label{er2cm2}$$
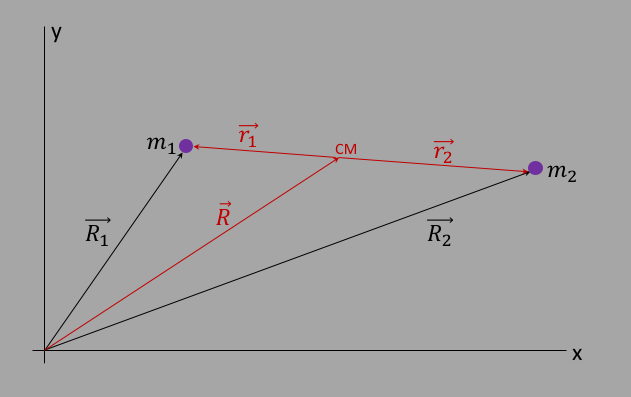
If we then plug these definitions into the definition for the vector $\vec{R}$ that points to the CM (equation $\ref{evecRR}$), we get the nice relation: $$M\vec{R}=m_1\vec{R_1}+m_2\vec{R_2}=m_1(\vec{R}+\vec{r_1})+m_2(\vec{R}+\vec{r_2}) = (m_1+m_2)\vec{R}+[m_1\vec{r_1}+m_2\vec{r_2}]=M\vec{R}+[m_1\vec{r_1}+m_2\vec{r_2}]$$ which can only be true if $$m_1\vec{r_1}+m_2\vec{r_2}=0\label{ercmcm}$$
Given that we now know how to describe the position of the CM, and the position of the satellites relative to the CM, we can now describe the velocities of the two satellites in a similar way. Starting with the diagram in figure 7 and the two velocities of the satellites relative to the origin, $\vec{V_1}$ and $\vec{V_2}$, we can form the analogous CM velocity analogous to equation $\ref{evecRR}$ via $$\vec{V} = \frac{m_1\vec{V_1} + m_2\vec{V_2}}{m_1+m_2}\label{evecVV}$$ and the relative velocities via: $$\vec{V_1}=\vec{V}+\vec{v_1}\label{ev1cm2}$$ $$\vec{V_2}=\vec{V}+\vec{v_2}\label{ev2cm2}$$ This is actually the same thing as considering the CM momentum, where we can define $P=MV=p_1+p_2$. Figure 7 shows how just like with the position vectors, the velocity vectors will add such that the CM velocity will lie on the vector $\vec{v}\equiv \vec{V_1} - \vec{V_2}$.
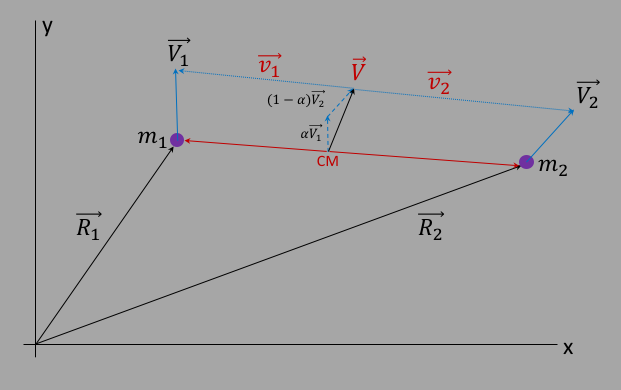
Now we can discuss the 2-body dynamics in terms of the angular momentum. First form the total angular momentum $\vec{L_{tot}}$ about the origin, and expand using equations $\ref{er1cm2}$, $\ref{er2cm2}$, $\ref{ev1cm2}$, and $\ref{ev2cm2}$:
| $\vec{L_{tot}}$ | $=$ | $m_1\vec{R_1}\times\vec{V_1} + m_1\vec{R_1}\times\vec{V_1}$ |
| $=$ | $[m_1(\vec{R}+\vec{r_1})\times\vec{V_1}] + [m_2(\vec{R}+\vec{r_2})\times\vec{V_2}]$ | |
| $=$ | $[m_1\vec{R}\times\vec{V_1}] + [m_2\vec{R}\times\vec{V_2}] + [m_1\vec{r_1}\times\vec{V_1}] + [m_2\vec{r_2}\times\vec{V_2}]$ | |
| $=$ | $[\vec{R}\times(m_1\vec{V_1}+m_2\vec{V_2})] + [m_1\vec{r_1}\times\vec{V_1}] + [m_2\vec{r_2}\times\vec{V_2}]$ |
The first term in the last line can be written as: $\vec{R}\times(m_1\vec{V_1}+m_2\vec{V_2})=\vec{R}\times M\vec{V}$ using equation $\ref{evecVV}$ and $M\equiv m_1+m_2$. This is clearly the angular momentum $\vec{L_{CM}}$ of the CM relative to the coordinate origin: $$\vec{L_{CM}} = \vec{R}\times M\vec{V}\label{elcm}$$ The last 2 terms in that line are not the angular momentum of the two satellites relative to the CM, which would be given by $L_1 = \vec{r_1}\times m_1\vec{v_1}$ and etc for satellite 2, however we can show that the sum of these last 2 terms is the sum of the angular momenta about the CM. To see this,d we can expand those last two terms using equations $\ref{ev1cm2}$ and $\ref{ev2cm2}$. For satellite 1, we have: $$m_1\vec{r_1}\times\vec{V_1}=m_1\vec{r_1}\times(\vec{V}+\vec{v_1})= m_1\vec{r_1}\times\vec{V} + m_1\vec{r_1}\times\vec{v_1}$$ When we add this to a similar term for satellite 2, we can easily see that the terms $m_1\vec{r_1}\times\vec{V}+m_2\vec{r_2}\times\vec{V}=(m_1\vec{r_1}+m_2\vec{r_2})\times\vec{V}=0$ using equation $\ref{ercmcm}$ above. This leaves the 2 terms $m_1\vec{r_1}\times\vec{v_1}$ and $m_2\vec{r_2}\times\vec{v_2}$, which are in fact the angular momenta $\vec{L_1}$ and $\vec{L_2}$ relative to the CM: $$\vec{L_1} = \vec{r_1}\times m_1\vec{v_1}$$ $$\vec{L_2} = \vec{r_2}\times m_2\vec{v_2}$$ This means we can write the total angular momentum $\vec{L_{tot}}$ as: $$\vec{L_{tot}} = \vec{L_{CM}} + \vec{L_1}+ \vec{L_2}$$ There are several ways to eliminate the angular momentum of the CM via choosing the right initial conditions, but the easiest is to just place the origin at the CM. Then $\vec{R}=$, which will make $\vec{L_{CM}}=0$
Back to initial conditions. We can give one or both of the satellites an initial velocity and start the simulation. However, if the net momentum of the satellites does not sum to zero, then the CM frame will have a momentum and a velocity, and you then see that the whole simulation would travel up the page. Not convenient for simulation purposes! To fix this, we will insert a correction to the initial velocities something that will ensure that the overall CM velocity remains 0. In otherwords, a boost into the CM frame. This is easily done.
First, we choose an initial velocity for the 2 satellites, call it $U_{i0}$ and $U_{i1}$ (we leave off the vector notation to make things easier to follow). Then, we make a boost (add velocity) $\Delta U$ to each one: $$V_{i0} = U_{i0} + \Delta U$$ $$V_{i1} = U_{i1} + \Delta U$$ such that we would have $m_1V_{i0}+m_2V_{i1}=0$. Following this through we will come up with $$\Delta U = -\frac{m_1U_{i0}+m_2U_{i1}}{M}$$
In the simulation below, you can vary the masses of the red and blue satellites, drag them both horizontally to change their locations, and drag the end of the arrow up and down to change the initial velocity of the red satellite. The green ball shows the CM location, and the cross shows the coordinate system center.
| $M_{red}$ |
| $M_{blue}$ |
| Scale by |
Many Body Dynamics | Back to top |
With more than 2 bodies, the equations of motion cannot be solved analytically. And as you can imagine, there's a science behind how to handle such many bodies in the influence of gravitational interactions. Below is an attempt to show many-body motion. If you click anywhere on the canvas, it will place a new satellite there, and prompt you for the mass and velocity. Note that the default is to have 2 masses of 100 and 1500 units, the smaller one has a positive velocity of 15 units up, the larger one is at rest. Whenever you create a new satellite, the velocity you give it will be in the azimuthal direction moving clockwise. The program will modify the velocities of all bodies so that the CM is not moving. Note that when displaying the satellits in motion, the program will connect them to the large mass at the origin with a yellow line, just so you can see what's happening. As you can see, it is not stable. But then, what is! :) I would suggest you use a lot of symmetry! (I will continue to add functionality, eg to slow down, change the scale, etc, just for fun...)
| Planet mass: |