A Physicist's Guide to Music, with some Math thrown in
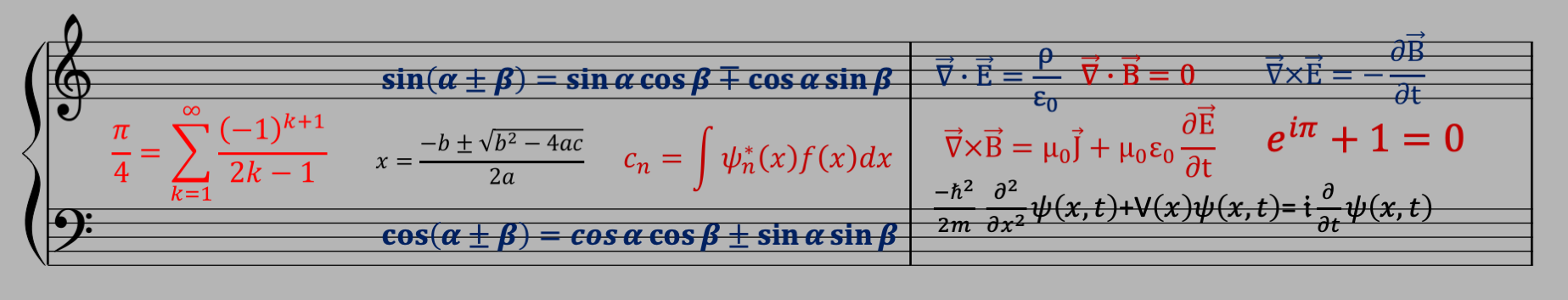
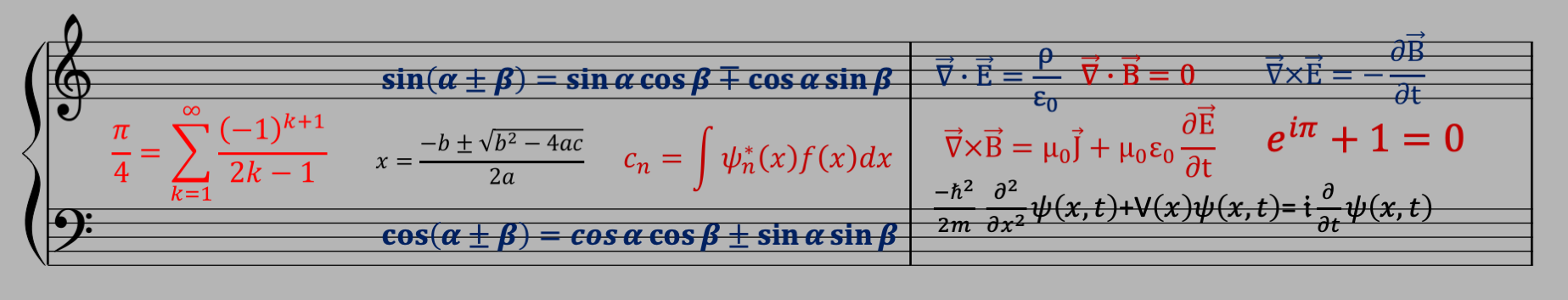
The whole subject of hearing, and music, and the way the human ear works and what the brain does with the input is somewhat of a miracle. And a huge subject. And it all starts with sound. So what IS sound?
We live in an atmosphere that contains a certain concentration of mostly oxygen (21%) and nitrogen (78%) with trace amounts of other gases, mostly argon (.9%) and carbon dioxide (.1%). But the concentrations don't matter - what matters is that it's a gas, and has a pressure and a density.
Pressure measures the force per area, so picture a box that is 1 foot on a side, and has 1 lb of stuff in it. If you place that box on a surface, the surface will have to sustain the weight of 1 lb, and it has to sustain that over the area of 1 ft$^2$ (1 square foot). The pressure at the surface of the earth ("1 atmosphere"), and is equal to 14.7 lb/ft$^2$, or 14.7 lbs of force on every square foot of area. This force comes from the weight of all the atmosphere directly above, which is amazing since the atmosphere extends 100s of miles high (but gets less and less dense as you go up). So if you took the column of atmosphere that is directly above the 1 square foot area, you'd have something that weighs 14.7 lbs.
Density measures mass per volume. The density of water is defined to be exactly 1 gram per cubic centimeter. This is actually how the gram used to be defined: make a volume of 1 cubic centimeter, and define the gram as the mass of the water in that volume. (Today, it has a much more robust definition, but that's another story.) 1 gm/cm$^3$ is equal to 1000 kg/m$^3$, which is equal to around 62 lbs per cubic feet at room temperature. That means a box that is 1 foot on a side will hold 62 lbs of water, whereas a box that is 1 square foot on a side and 100s of miles high will hold 14.7 lbs of air. Clearly air is less dense than water!
Ok so here's where sound comes in. Imgine you have a volume of air, and it's perfectly still - no wind. Now imagine you do something that causes a temporary increase in the pressure at some location at the edge of the box. What happens is that this increase of pressure compresses the air. Think of the air as a bunch of molecules all connected by springs on both sides in rows, as in the following figure:
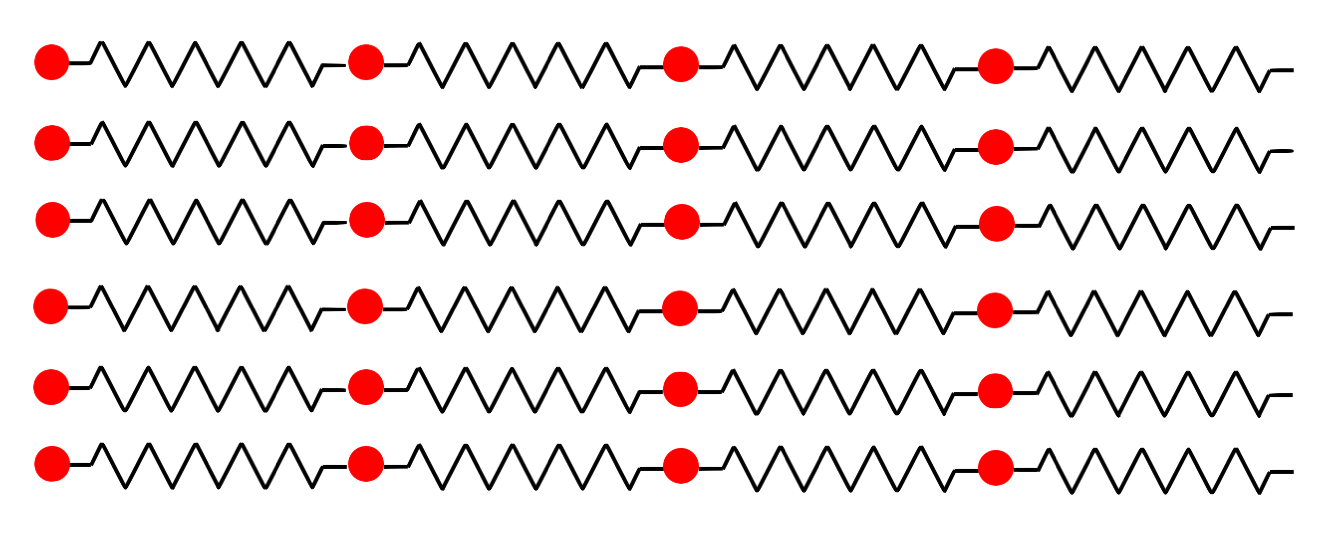
If we push on the molecules on the left side and then release, this compresses the springs, and is equivalent to a temporary increase in pressure starting from the left:
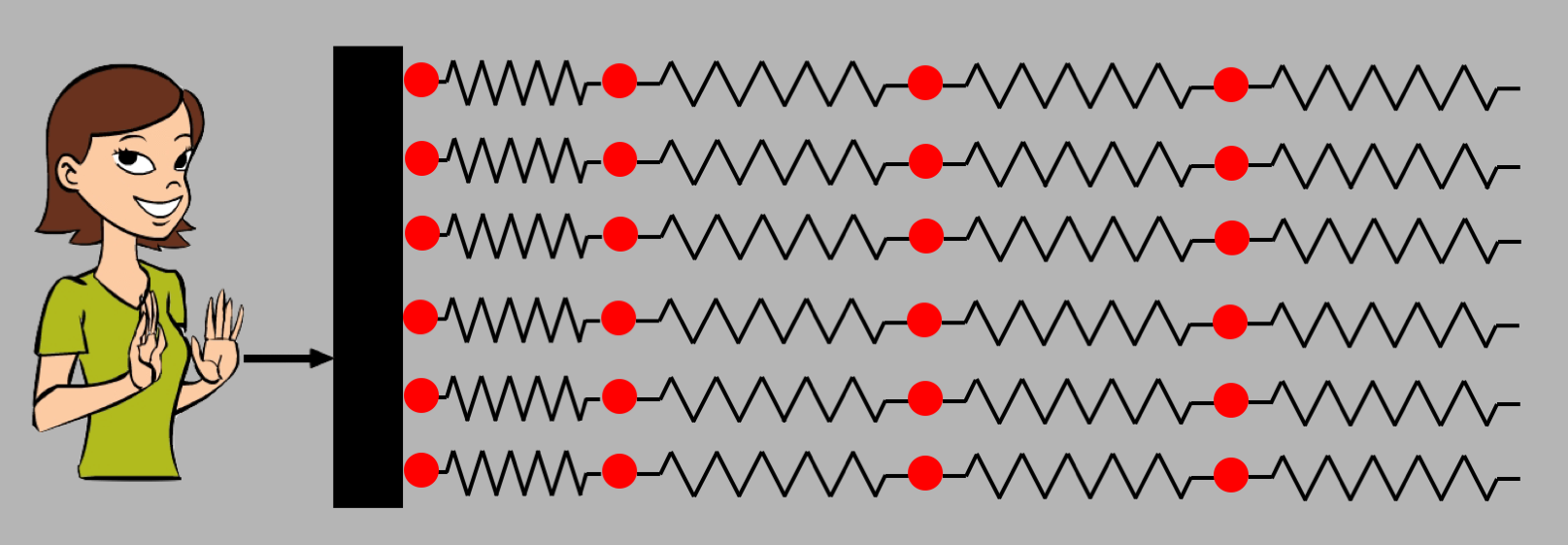
The springs then push on the 2nd column of air molecules, compressing the second column of springs and relaxing the first:
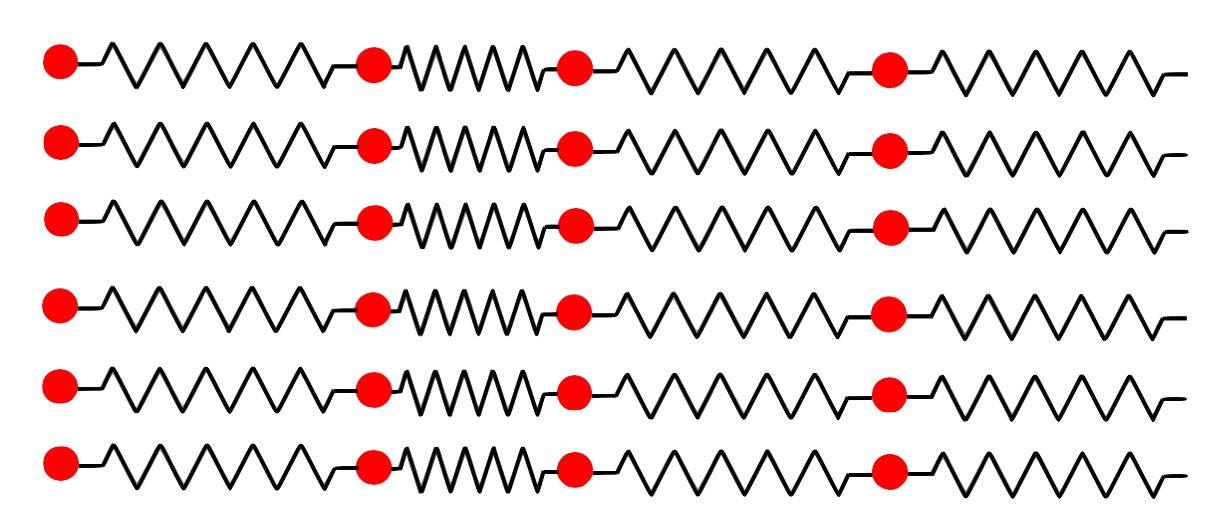
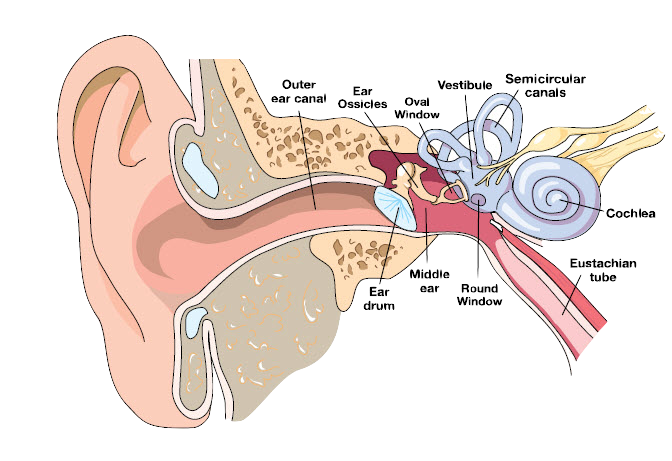
And that compresses the next column to the right, and so on. This compression, or "disturbance", propagates from left to right, and when it gets to your ear it travels down the outer ear canal until it compresses the "ear drum", which is basically a membrane border to the outer ear. On the other side of the ear drum is some complicated machinery that turns the motion of the ear drum into electrical signals that are sent to the brain, and voila, sound.
A sound wave is nothing more than a disturbance in the pressure that propagates. The medium can be anything - the air, water, even solids, but not vacuum (remember the ads for the 1979 movie Alien that said "In space, noone can hear you scream"!).
The speed of this disturbance depends mainly on two general properties of the medium: the elasticity (how "stiff") and the density. In our spring analogy, the elasticity is the "springiness" (spring constant) and the density is the mass of the molecules per volume. In a gas like air, the density is a function of temperature, but the elasticity (called the "bulk modulus", $K$) tells you about the resistance to compression, and is pretty much constant and depends on the medium. For air, the bulk modulus is around 1 atm (1 atmosphere), whereas for water it's around 22,000 times greater, and for steel it's almost 80 times larger than for water. The density ($\rho$) of air is approximately $1.23 kg/m^3$, whereas for water is it $1000 kg/m^3$ ($813$ times greater) and for steel it's $8,000 kg/m^3$. The speed of sound in air at standard temperature and pressure is $343m/s$ or $760mph$. It turns out that the formula for the velocity of sound in a medium goes like $v=\sqrt{K/\rho}$, which means the speed of sound in water is greater than that in air by a factor of $\sqrt{22,000/813}=5.2$, or around $1700m/s$! For steel, it's $\sqrt{80/8}=3.2$ times greater than for water! That the speed of sound is so much greater in these denser mediums is due to the elasticity of the medium: steel is very "stiff", which means it springs back very quickly, so the disturbance travels very fast.
Sound is a pressure wave, and the propagation is in the same direction as the disturbance. This is why sound is called a "longitudinal" pressure disturbance. Note that waves can be either "longitudinal", where the disturbance is along the propagation and "transverse", where the disturbance is perpendicular to the propagation. Ocean waves are transverse, sound is longitudinal.
The following demonstrates the longitudinal propagation of a pressure disturbance. Between each blue gas molecule is a "spring" (it's actually the force between 2 molecules in the air, which we can model as a spring). When you hit the "Press" button, you cause the disturbance on the left molecule to compress the spring next to it, and at some point that compression causes the spring to compress the molecule on its right, which decompresses that spring and compresses the next one on the right of the 2nd molecule. And so on from one molecule to another as the wave propagates left to right.
The sounds we hear can take many different forms. Some are due to things banging together, and some are heard as tones, or notes, etc. The difference is that the sounds (the notes) we hear for music are sounds that are periodic waves, and waves have lots of properties we want to understand before we get into music and music theory.
A wave is something that is repeats, and so is "periodic". The "period" $T$ of the wave is defined as the time for 1 cycle, which repeats, so has units of seconds, and is the number of seconds per cycle. We also define the frequency $f$ of the wave as the number of cycles in 1 second. Since $T$ is seconds per cycle, and $f$ is cycles per second, we have the relationship: $$f=\frac{1}{T}\nonumber$$ Note that the units of frequency, cycles per second, are also refered to as a "Hertz" named after the 19th century physicist Heinrich Hertz who studied electromagnetic waves. The unit of frequency is usually denoted as 1 cycle per second = 1 Hz (1 hertz).
So, if someone plays a note, it will have a particular frequency $f$ and period $T$, which means that if you were to be a 2mm tall person standing at the ear drum, you would "see" a pressure disturbance that repeats over a time $T$, with frequency $f$. But what does that mean that you "see" a repitition? It's the repeating of the pressure "amplitude", which we can call $p$. The pressure will have a maximum and a minimum, which we will call $P_0$. So more definitivley, you will see the pressure rise to a max $P_0$, fall to a min $-P_0$, and rise back to the starting point and then repeat. The reason why the min is $-P_0$ is because the pressure on the ear drum can be either towards the drum pushing it in (positive pressure) or away from the drum pulling it out (negative pressure). So the pressure varies between $\pm P_0$, during the time $t$, and the repeating happens over a time $T$.
Mathematically, we can express the pressure amplitude as a function of time $t$ at that point near the ear by the formula: $$p(t) = P_0 g(at)\nonumber$$ Here we have a general function of time $g(at)$ that varies between $-1$ and $+1$ so that $P_0\cdot g$ is the min and max pressure. We want $g$ to repeat after a time $T$.
It turns out that a pure tones are labeled by its frequency, and repeat sinusoidally, which means we can use the trig functions $\sin$ and $\cos$ for the function $g(at)$: $g(at) = \sin(at)$. Since we want $g$ to repeat after a time T, that means we have $\sin(a[t+T]) = \sin(at)$, or $\sin(at+aT)=\sin(at)$, which means that $aT=2\pi$ since the sine and cosine function repeat after $2\pi=360\deg$. Solving for $a=2\pi/T=2\pi f$ we have the pressure wave as: $$p(t) = P_0 \sin(2\pi ft)\nonumber$$ or as is traditional, we substitute $\omega = 2\pi f$ ($\omega$ is called the "angular frequency") and write $$p(t) = P_0 \sin(\omega t)\nonumber$$ For those who need a refresher course on trigonometry, try here. But the basics are that the pressure disturbance for notes propagates sinusoidally from one location to another. And music consists of hearing notes, one after another, with different frequencies.
One of the more interesting (of many) things about music is that when we hear it, we are
often hearing more than one note at a time. The difference in frequency between the notes
is called the "interval", and how the brain makes sense of intervals is one of the miracles
of music.
To begin this discuss, consider the mathematics of hearing 2 notes at a time. This means
that 2 pressure waves hit your hear simultaneously.
So say the two notes are characterized by the two pressure waves $p_1$ and $p_2$, with
frequencies $\omega_1$ and $\omega_2$. Let's imagine for the time being (to make the math
easier) that the amplitudes of the two waves are the same: $P_0$. Then the two waves are
$$p_1(t) = P_0\sin(\omega_1 t)\label{ep1}$$
$$p_2(t) = P_0\sin(\omega_2 t)\label{ep2}$$
The wonderful thing about waves is that they add linearly. That is, the total pressure
$p$ is equal to the sum of the 2 pressures:
$$p(t) = p_1(t) + p_2(t)\label{epsum}$$
It's not so obvious that this would be so! Why wouldn't it be, for instance, $p = p_1\times p_2$
or something other than $p_1 + p_2$. That's another story! Anyway, what's the math of
$p = p_1 + p_2$? Let's take equations $\ref{ep1}$ and $\ref{ep2}$ and plug them into
$\ref{epsum}$:
$$p(t) = p_1(t) + p_2(t) = P_0\sin(\omega_1 t) + P_0\sin(\omega_1 t) =
P_0\Big[\sin(\omega_1 t) + \sin(\omega_2 t)\Big]\nonumber$$
We can unravel $\sin(\omega_1 t) + \sin(\omega_2 t)$ by making the following definitions:
$$\omega_{av}\equiv \half(\omega_1 + \omega_2)\label{oav}$$
$$\delta\omega \equiv \half(\omega_1 - \omega_2)\label{dom}$$
If we solve for $\omega_1$ and $\omega_2$ in the 2 equations above, we get
$$\omega_1 = \omega_{av} + \delta\omega\nonumber$$
$$\omega_2 = \omega_{av} - \delta\omega\nonumber$$
Substituting into $\ref{epsum}$ gives
$$p(t) = P_0\cos(\delta\omega t)\sin(\omega_{av}t)\label{ebeat}$$
Interference
Beats
Back to top
What's interesting about this equation is when you have 2 frequencies, $f_1$ and $f_2$, that are close together. For instance, say $f_1 = 220$Hz and $f_2 = 222$Hz, then we have $f_{av} = 221$Hz and $\delta f=1$Hz (where we have used $\omega = 2\pi f$). In this case, we can write equation $\ref{ebeat}$ like this: $$p(t) = P(t)\sin(\omega_{av}t)\nonumber$$ It looks like a single waveform with frequency $f_{av} = \half(f_1+f_2)$ but with a slowly varying amplitude $P(t)=P_0\cos(\delta\omega t)$. We call $\delta f=\half(f_1-f_2)$ the "beat frequency": $$f_{beat} = \delta f = \half(f_1-f_2)\label{fbeat}$$ Note that we could easily have defined things so that $f_2$ is greater than $f_1$, giving a negative beat frequency, however remember that the cosine is an "even" function, which means $\cos(-x)=cos(x)$, so it doesn't matter if the frequency is positive or negative, the cosine will not care.
To get a better feel for it, in the simulation below, you will see 3 plots, all as a function of time. The top shows the waveform for a wave with amplitude 1 and frequency preset to $f_1=$200Hz (and period $T_1=1/f_1=f/200$Hz$=5$ms). The left text box above the plots allows you to change the frequency $f_1$, and if you click the little checkbox it will play the tone as a sine wave. The 2nd plot shows another wave with a different frequency, preset to $f_2=202z$ (and period $T_2=1/f_2=f/202$Hz$=4.95$ms), with the same text window to change the frequency and checkbox to play the tone. The 3rd plot is simply the sum of the two waveforms as a function of time, with the beat frequency overlayed in blue to show the $P_0\cos(2\pi f_{beat}t)$ amplitude function explicitly. The average frequency will be the average of 200Hz and 202Hz: $f_{av}=201$Hz. The beat frequency will be given by half the difference between the two: $f_{beat}=1$Hz. You can move the slider value around to "zoom" in and out, so as to better see how the beat frequency modulates the average of the 2 tones. It is preset so that you can see 4 or 5 periods of the two individual waveforms, but since the beat frequency is 1Hz, then that means the modulation will have a period of 1 sec which is 200 times greater than the period of either waveform, so you will have to move the slider up to around 200 or more to see the beat envelop. What you should see, and hear if you click on both checkboxes, is a single tone modulated by the beat frequency. One thing to notice: you will hear the modulation rise and fall twice as fast as the amplitude modulation in the plot, but this is because the modulation amplitude goes through 2 maxima for 1 period of oscillation (which is why the blue curve is drawn above and below the waveform). It's a subtle thing, and sometimes people define the beat frequency as just the simple difference between the 2 frequencies. So you have to be careful with definitions!
One last thing to mention before you play with the simulation: on my MacBook Pro, I find that it cannot play any tone that has a frequency smaller than around 150Hz through the speakers. That is, it can play it, but you won't hear it. But the audio output is pretty good, so if you use headphones instead of the speaker, it will work fine down to almost 10Hz, which is pretty good. It will also go way up past 10kHz, but given my age I couldn't hear anything much over that, however you can try it and give yourself a hearing test although you should probably start with the volume down to around half full just to be careful
Music is an amazing phenomena. It connects the physical - sound waves - to the brain, and what emerges out of that is art, beauty, feelings. And underlying music is some very interesting mathematics.
And the mathematics starts with the famous Greek philosopher and mathematician, Pythagoreas, the same one with the famous theorem relating the length of the sides of the right triangle (see the chapter on trigonometry). He was born around 570 BC on the island of Samos, just off the east coast of Turkey, and died in 495 BC. His life is somewhat of a mystery due to the paucity of materials. He was an early philosopher and mathematician, influencing Aristotle and Plato. When he was around 40 years old he relocated to the Italian town of Croton, which is located all the way at the bottom of the "boot". It was in Croton where he established a school, or perhaps more like a religious order, to study mathematics and nature. It is said that this school was shrouded in mysticism, and played a political or perhaps even a religious role in local events. One story I read once said that the local townspeople were afraid of the mystics at the school, and that after Pythagoreas died, they stormed the school and killed everyone there. This is probably one of those stories embellished over the centuries for some purpose, and probably not true as their are conflicting accounts of how he died and what happened after. But it would probably make a good movie! :)
What Pythagoreas and the Pythagoreans did was to think of mathematics as a secret, perhaps mystical way to understand nature, creation, the whole idea of gods and man's relationship to those gods. They believed that mathematics was perfect, and represented the true nature of reality at its deepest. In this they were the precursors to Plato and his philosophy of nature and god based on perfection. They also believed in the existence and perpetuation of the soul after death, were vegetarians, and accepted women as well as men into the school.
The Pythagoreans studied geometry, and from that study came the Pythagorean theorem and a host of other facts concerning right triangles, for instance the sum of the interior angles, how to construct "regular" solids, some astronomy, and so forth. And they studied numbers, specifically integers although there is some evidence that they also studied (or even "discovered") the "irrational numbers", which are fractions that cannot be represented as the ratio of 2 integers. They believed that the key to understanding nature, and life, and everything about existence was achieved by studying numbers, that numbers were fundamental to everything and contained all the information you needed to know. They studied odd and even, and attributed meaning to each of the integers and even various sums of integers (10 is the "perfect" number because it is the sum of the 1st 4 integers).
It is likely that the study and appreciation of integers played a role in the Pythagorean study of music. They made observations on vibrating strings, and how the pitch was proportional to the length of the string (as you can see by pushing down on a guitar or violin string). They made the connection between the relationship between the length of the vibrating string (the actual note, although they did not know about "frequency"), and investigated intervals and harmony. And they noticed that playing two strings where the ratio of the lengths is given by a ratio of integers (such a number is called a "rational" number) was much more harmonious than if the ratios were not integers (irrational). Actually, you can characterize almost any fraction as the ratio of integers. For instance, 0.5502 can be written reasonably accurately as the ratio of 13579 divided by 24680. But the Pythagoreans did not have calculators, and probably they were saying that when the ratio of the lengths were the ratio of small integers, it was more harmonious.
To see this yourself, you have 2 waveforms in the simulation below. The top is A4 (220Hz), as is the bottom initially. But if you drag the yellow ball to the right, you can decrease the bottom wavelength, equilalent to pressing your finger on the kneck of a stringed instrument like a violin. This increases the frequency, and the ratio of those frequencies is reported as a real number with 3 decimal places. When you hit "Start", it will oscillate the waveforms and play a tone proportional to the frequencies (the top waveform stays at 220Hz). Note that you can't change the bottom tone to be greater than 2x the top (A440). You can hear the two tones played together, and see for yourself if you agree that the interval (the 2 tones) is more harmonious or not if the ratio of lengths, which is the same as the ratio of the frequencies, is the ratio of 2 integers (e.g. 2:1 = 2.000, 3:2 = 1.500, 4:3 = 1.333, 5:4 = 1.250, etc).
Ratio of lengths: 1.000 = 1/1
To see this, the simulation below will play 2 tones with different frequencies through the computer speaker. The code plays the tone at 10% of volume, and that can mean different things for different computers and browsers. So you might have to turn your computer sound volume up or down as needed. The two tones start out at the same frequency, 220Hz, which is A in the 4th octave (depending on how you count, but it's the 4th A on the piano). The x-y plot with the circle will have 2 small balls, colored blue and red, and each ball will go around the circle at a rate proportional to its frequency. The blue ball is fixed at 220Hz, but you can vary the red ball in several ways to see what happens. If you click on "Manual" in the radio buttons, then you can use the slider to change the frequency. You click the "Start" button to start, "Stop" to stop (pause), and "Reset" to put things back at the beginning. If you click any other radio button, it will set the red frequency according to the ratios shown (x2, x3/2, etc), which are ratios of integers. You can see that when the ratio of the frequencies are ratios of whole numbers (integers), the two balls eventually coincide at the same place where they started together (on the cirlce, due "east"). For instance, if the ratio of the two frequencies is a factor of 2 ($f_1=220$Hz and $f_2=440$Hz), then the red ball goes around twice for every once around for the blue. When the ratio is 3/2 ($f_1=220$Hz and $f_2=330$Hz), then for every 3 trips around for red, blue goes around 2 times. But that at some point, they coincide. The top row allows you to set any interval between the 2 frequencies (click on "Manual"), or you can set 2/1, 3/2, 4/3, and 5/4 and it does the adjustment for you. The counter just above the circle counts the laps between resets.
$f_1=220$Hz $f_2=$ 220Hz
Laps: 0 0
Chords in music are when you play more than one note at the same time, so there's an interval between the two frequencies. And the idea of an interval is key concept in music. What Pythagoras and company discovered is that the chords (intervals) that sound the most pleasantly harmonious are chords where the ratios of the lengths of the strings (which is the same as the ratios of the frequencies) are ratios of integers: $$L_2/L_1 = n/m\nonumber$$ where $n$ and $m$ are both integers (1,2,3,...). Such a ratio is called a rational number. And the Pythagoreans noticed another interesting fact: that when the intervals are given by 3:2 (the larger length is 3/2, or 1.5 times the smaller length), the interval is particularly harmonious.
Pythagoras and his followers did not know about the physics of sound, and how the fundamental thing that differentiates one note from another is the frequency of the oscillation, as described above. But for vibrating strings, there's a direct relationship between the length of the string, and frequency, as long as the tension in the string stays constant. If you want to understand this relationship, read on, but if you want to skip this and get right to the idea of harmony and integers, click here.
To illustrate, let's consider the cello (it's the same for all stringed instruments):
The string is fixed at the Peg and by tightening, you can increase the tension in the string. The string is also fixed at the bottom end of the cello, sometimes in the Fine Tuner and sometimes just fixed to some other mechanism. If you have a Fine Tuner, you can also change the tension by tightening. Between the Peg and the Fine Tuner, the string will go over the Bridge and the Nut, and those locations are called "nodes" (more on this later). If you pluck the string between the Bridge and the Nut, it will vibrate, but there will be fixed points (called nodes) at those 2 locations. This is key. The distance between the nodes of a vibrating string is what Pythagoras and friends used for the length as discussed above.
A perfect note will be a sine wave, so for the sake of simplicity, let's assume perfectly sinusoidal vibrations. We have 3 quantities, all related, that characterize the vibrating string:
As discussed above, the principle of interference says that when you have two different waves (propagation of a disturbance) in a medium, the resultant wave will be the sum of the individual waves: they add linearly. Mathematically, let $y_1(x,t)$ be the wave function of the first wave, and $y_2(x,t)$ be the wave function of the second. It doesn't matter whether the wave shapes are described by a sine, cosine, or any other shape. When you add them together you get: $$y_{sum}(x,t) = y_1(x,t) + y_2(x,t)\nonumber$$ The principle of superposition is one of the most basic and important laws of nature, important in all the natural sciences, including engineering. But that's another story.
Next let's consider a "traveling" wave, which is pulse moving from left to right with velocity $v$ in a reference frame we call $O$. Running alongside the pulse with the same velocity $v$, you would then be in the stationary rest frame $O'$, and see a stationary pulse that would have some shape, described by function $f(x')$ where $x'$ is the coordinate along the direction of motion in the moving frame $O'$. $f(x')$ is not a function of time $t$ since the pulse is not moving in this frame. The situation might look something like the following simulation. The checkbox can be used to show explicitly the $O'$ frame, and the relationship between $x$ (the coordinate in the stationary frame $O$), and $x'$, the coordinate in the moving frame $O'$.
Show $O'$
To get the functional form of the pulse in the stationary frame described by the coordinates $x$, all you have to do is use the fact that a point $x$ in the stationary frame ($x$ is the distance from the y-axis in that frame) is related to a point $x'$ (the distance from the moving y-axis in the moving frame) by the relation $x = x' + vt$. Using $x' = x - vt$, we can write down the wave equation for a moving wave as $f(x') \to f(x-vt)$. This describes the wave moving left to right. For a wave moving right to left, we simply replace $v$ with $-v$ and get $f(x+vt)$ as the wave equation.
Now let's see what happens when the wave is sinusoidal. Let's say that in the moving frame, we have $f(x') = A\sin (2\pi x'/\lambda)$ where $A$ is the "amplitude" and $\lambda$ is the wavelength, defined as the distance over which the wave repeats itself. To make things simpler, we define the quantity $k\equiv 2\pi/\lambda$ ($k$ is sometimes called the "wave number"), which gives us $f(x')=A\sin(kx')$. This gives us the wave equation in the stationary frame: $$f(x,t)= A\sin k(x-vt)=A\sin (kx - kvt)\nonumber$$ We can define the period $T$ as the time over which the wave repeats, and the quantity $kv=2\pi v/\lambda$. If the wave is moving with velocity $v$, then it will take $T$ secconds to cover a distance $\lambda$, which means $v =\lambda/T$, which means $kv=2\pi/T\equiv \omega$ where $\omega$ is called the "angular velocity". This gives us the equation $$f_R(x,t)= A\sin (kx - \omega t)\nonumber$$ for a wave moving to the right, and $$f_L(x,t)= A\sin (kx + \omega t)\nonumber$$ for a wave moving to the left.
Now we can analyze what happens when two waves moving in opposite directions interfers to form a new wave. The math is easy, although a little messy. From the principle of superposition, the sum $f_S(x,t)$ will be given by $f_S(x,t) = f_R(x,t) + f_L(x,t)$. If the waves are both sine waves with the same wavelength, we can write: $$f_S(x,t) = A\sin(kx-\omega t) + A\sin(kx+\omega t)\nonumber$$ Using the trig formula $\sin(a\pm b) = \sin a \cos b \pm \sin b \cos a$, we have $$f_S(x,t) = A(\sin kx \cos \omega t - \sin \omega t \cos kx) + A(\sin kx \cos \omega t + \sin \omega t \cos kx) = 2A\cos\omega t\sin kx$$ If you stare at this formula long enough, you can see that this represents a wave that has the spatial sinusoidal shape $\sin kx$ with an amplitude that $2A\cos\omega t$ that is changing over time. This is called a "standing wave": the functional form just "stands there", but the amplitude oscillates over time. This is a general property of opposite going traveling waves: they interfere to form standing waves, and this is shown in the following simulation.
Now we want to understand what happens when a wave pulse traveling to the right hits a boundary,
remembering that a wave is the propagation of a disturbance on a string, and that at the boundary
(aka "node"), the string is constrained to not move ("fixed"),
like a violin or a cello, as described above. In the figure
below, a string is attached at the yellow wall, and a pulse
is sent from the left side to the right.
This pulse could have been initiated by someone pulling on the string, and letting go.
As it gets to the right boundary, it is
reflected, and inverted, and reverses direction, propagating to the left. What we want to
understand is why the inversion.
The reason for the inversion starts with the fact that a pulse (wave) is really the
propagation of a "disturbance". So when you lift up the string, you've stretched it like
stretching a spring from its equilibrium position. The top point of the string (where
you are holding it before releasing) will exert a force on the infinitesimal piece
just to the right and
that force will want to raise that piece. That piece will pull on the next infinitestimal
piece just to its right, and so on all the way down to the boundary.
At the boundary, where the string is fixed, there's no way for the piece connected to the
boundary (node) to rise up, so it stretches and pulls back (reaction). When the center of the
disturbance gets to the boundary, the inertia of the piece connected to boundary will cause
an overshoot, producing a negative pulse.
This is somewhat of a simplistic "hand waving" explanation,
and to see the exact form of what happens at the boundary you need more extensive analysis,
and a simulation to help visualize, as is shown below. A key concept here
is that you start with a wave pulse traveling to the right, and impose a boundary condition
at the yellow wall where the string is attached:
the string is fixed at that point, and therefore cannot move. So as the wave hits the wall,
what happens to it? Where does the energy go?
There's a nice trick, used all the time in physics, to show what happens, and this is
shown in the simulation below. Let's call the region to the left of the yellow wall the "real"
region, and the region to the right the "ghost" region.
Imagine that in the ghost region (inside the wall), we have
a similar pulse, inverted relative to the initial pulse in the "real" region, moving from
left to right in a symmetrical way. Both pulses have the exact same shape (the "ghost" wave
is inverted), and they are equidistant from the boundary traveling towards it initially.
In such a situation, both pulses hit
the boundary at the same time (the "ghost" pulse was constructed that way), and from the
principle of superposition, the resulting pulse (the one in blue) is the sum of the "real" and
the "ghost" pulses. Since they have opposite polarity, they cancel each other out, resulting in
no motion at the boundary, which is exactly what the node boundary condition requires.
So from a physics (and mathematical) point of view, we can add this "ghost" pulse to the
simulation, not changing anything in the "real" region (which is
where we are!), and it will enforce the boundary condition. But then after both pulses
each the boundary, the "real" pulse disappears into the "ghost" region (moving to the right),
and the "ghost" keeps moving to the left in the "real" region. So from the point of view
of someone in the "real" region, the pulse initially moves tothe right towards the boundary,
and bounces off inverted, moving to the left. Note that you can also derive this result
by analyzing the forces on infinitestimal pieces of string as the pulse moves, and with
the help of some mathematics show that because the string is attached to the wall, Newton's
law will cause the reflected pulse to be inverted.
In the simulation below,
the "real" pulse is on the top, the "ghost" pulse is on the bottom, and the pulse that
we see in blue is the sum of the two pulses in the "real" region: initially, the blue pulse
is the top pulse, but after both pulses cross the boundary, the "ghost" pulse is now in the
"real" region, and the real pulse is therefore inverted. Hit the "Start" button
below and see what happens - when the "ghost" gets to the left side, the simulation stops, so
hit "Reset" to "Start" it again. The pulse shown has a gaussian shape, with the width
determined by the value in the slider. The initial width is 20 (arbitrary units).
Pulse Width:
20
It is interesting to use the slider to increase the pulse width, and rerunning the simulation.
As you make the width large, compared to the interval of the string (try 150, or even 300),
you can see that the situation less resembles a pulse reflecting off a boundary, and more
of a wave that is oscillating, attached to the wall. Like one end of the jump rope, except that
whereas for a jump rope the energy is continuously being pumped in,
in the case we are simulating above, it's just a single pulse.
So for single pulses, reflection at a boundary that has a node causes an inverted pulse to travel
backwards.
Now lets extend this to the situation where you are driving pulses onto a string continuously,
they are traveling to the right, and they reflect inverted at a boundary. As we have shown,
we can substitute an inverted left traveling pulse for the reflected pulse, so the two pulses
will interfere, which will cause a standing wave with a node at the boundary. But for string
instruments, there are 2 boundaries, one at each end, so we need the standing wave from the
interference of all the waves bouncing around to have nodes at both ends, and this is easy
to do: just make sure that the wave nodes match the nodes of the string where it is attached
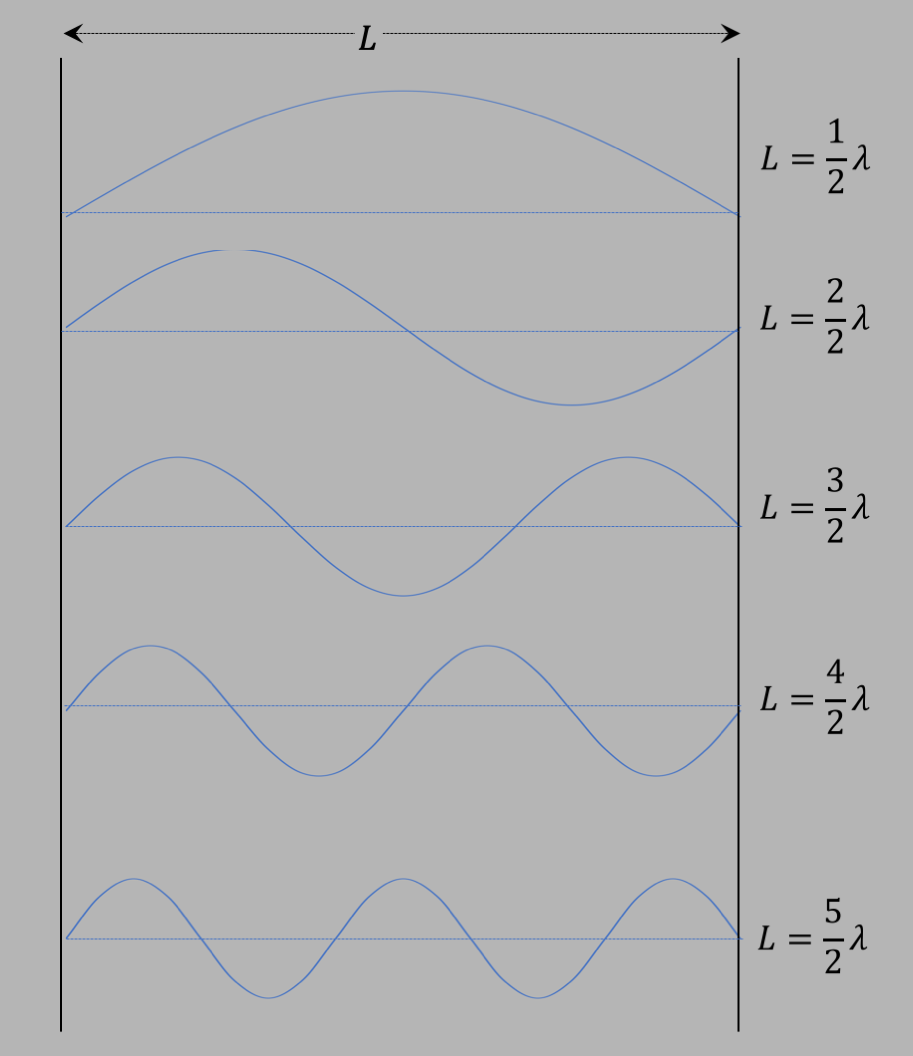
to the walls. Since one full wavelength of a sine wave has nodes at the beginning
($\theta=0$), the middle ($\theta=\pi$), and at the end ($\theta=2\pi$), then if we have a
wave of wavelength $2L$ where $L$ is the distance between the walls, we will get a standing
wave that matches the boundary condition with $L=\half\lambda$.
However, if you have a wave with wavelength $L=\lambda=2\half\lambda$, that will also fit.
And for that matter, $L=\lambda + \half\lambda = 3\half\lambda$ will also fit, as will
$L=2\lambda=4\half\lambda$, and so on. See the pattern?
So in general, you will get standing waves, which means constant vibrations, when the
condition:
$$\lambda_n = \frac{2L}{n}\label{lquant}$$
is met.
The wavelength is written as $\lambda_n$ to reflect the fact that the wavelength $\lambda$
is "quantized", or more accurately, "discrete".
Such phenomena is quite common in nature: when you have waves and boundaries, you get quantization!
If we use the formula $v=\lambda f$ where $f=1/T$ is the frequency (cycles per second)
and $T$ is the period (seconds per cycle), we get the equation
$$f_n = n\frac{v}{2L}\label{fquant}$$
What determines the velocity of waves on a string? As you can imagine, waves won't propagate
very fast on a loose string, whereas they will go faster for strings that are pretty tight.
You can try this with a rope, the effect is clear. The other thing that will affect the
velocity of distrubances will be the mass per length of the string. This is simply a
consequence of Newton's law $\vec a = \vec F/M$: the disturbance is a force, and the bigger
the force the more movement in the string and the greater the propagation of the disturbance.
So it's natural to guess that the less mass of each infinitestimal peice of string, the faster
the disturbance would propagate. If the tension in the string is given by $T_F$, and the
mass per length is given by $\mu = M/L$, then the velocity should be a function of the ratio
$T_F/\mu$. Actually, a real analysis will show that
$$v=\sqrt{T_F/\mu}\nonumber$$
The ratio $T_F/\mu$ is telling you something important: the movement on the string is the
ratio of the "elastic" force ($T_F$) to the inertial force ($\mu$). This happens all the
time in physics!
What happens in a violin, or a cello, or any other string instrument, is that when you
pluck the string, you send a wave that moves down the string and "bounces" off the fixed
point. If you pluck it, what happens is that as it keeps bouncing back and forth, it
loses energy, and this is manifested as a "smoothing" out of the wave (the higher frequencies
die off faster than the lower ones). You will still get interference of the right and left
moving waves as they bounce around. If you bow the string like with a violin, it sets
up continuous waves that travel, bounce, and interfere with each other. For either case,
those waves that have wavelengths (or frequencies, same thing) that
satisfy the boundary condition in equation $\ref{lquant}$ will form standing
waves, and those that have nother wavelengths that won't "fit" will just die away quickly.
Tuning a string is simply a matter of changing the tension $T_F$, so that you get a higher
or lower wave velocity. The constraint is that the string have a fixed length between
the nut and the bridge. So changing the tension will change the velocity, which changes
the frequency, hence the note. The fine tuner at the bottom of the violin is used to
adjust the tension with some fine control, but sometimes it's not necessary and not all
violins, cellos, etc have fine tuners.
One more thing. The bridge is between the top of the violin body and the string, so when
the string vibrates, it pushes down on the body in a sinosoidal fashion using the bridge
to transmit the force. This means that the body will vibrate pretty much in unison with
the string. That vibration sends out pressure waves with pretty large amplitudes (the whole
body is vibrating!) and that's where the sound that you hear comes from. The "f-hole"
on the body allows air to move in and out so that the vibration isn't compressing air, and
losing energy, saving the energy for vibrating the body.
The idea that harmony and the ratios of integers are related to each other says something deep
about the nature of music, and the human brain. There has been a huge amount of work on this
(a good introduction can be found by reading Oliver Sacks' book Musicophilia). There is
some evidence that music and language are intimately related, from neuroscience studies, and
as detailed in Sacks' book, there are documented cases of musical abilities appearing after
hits by lightening, or from the beginning of seizures. It is a fascinating subject, but
it is not my subject!
However it is interesting, from a mathematical point of view, that from these observations
on harmony and the ratios of frequencies, we have a very elaborate and beautiful theory of music.
Had it turned out that harmony was based, instead, on the difference in frequencies (and not
the ratio), the entire phenomenon of music, harmony, and music theory would have turned out
entirely different (perhaps we would have a different theory for different frequency ranges!).
Now that we understand waves, how they interfere, how they form standing waves, etc, it's time
to start learning about the theory behind how waves and sound lead to music: music theory.
The first thing to know in music theory involves what are called "intervals", which are 2
notes with differnet frequencies, played together, described above,
and as Pythagorus and others discovered, some intervals sound better than others, so those
"nice sounding" intervals, that come up all the time, have names.
The first intervals to discuss is called the "octave":
2 notes that are have frequency ratios of 2:1.
So if you have a note, then the next note an octave above will hava a frequency
x2 higher, and the octave above that will be x4 higher than the original. For instance,
if you start with the lowest note on the piano, A0 = $27.5$Hz, then A1 = $55$Hz (x2) and
A2 = $110$Hz which is x4 A0. And so on, so that we can write the formula
$$A_n = A_0\cdot 2^n\nonumber$$
The piano has a 7 octave range, which
means that the highest A on the piano, A7, is $2^7=128$ times A0, or $3520$Hz.
The human ear hears frequencies between $20$ and $20000$Hz ($20$kHz), a range of a
factor of 1000, which is pretty close to $2^{10}=1024$, which is why we say that the
human ear has a 10 octave range.
The interval where the two frequencies are related by the ratio 3:2, or 1.5,
is called a "fifth"
(more on where that comes from later). Let's use the modern terminology (which probably goes
back a few hundred years): the lower freqency of the pair
is called the "tonic" ($f_t$), and the higher frequency is called the "dominant" ($f_d$), and
so by definition $f_d/f_t=3/2$.
To illustrate, we can start with A0 as the tonic (say $f_0=27.5$Hz), and construct the fifth by
adding a dominant with frequency $f_1=1.5\cdot f_0 = 1.5\cdot 27.5=41.25$Hz.
Then we construct another fifth with
$41.25$Hz as the next tonic, with
dominant $f_2=1.5\cdot 41.25=61.88$Hz. And so on all the way up.
It is interesting to compare octaves and fifths. As shown above, if we start with
the note $A0$ ($f_0=27.5$Hz), the 7th octave above A0 will be A7 with frequency that
is $2^7$ times greater, or
$f_7=2^7\cdot f_0$ = 128*27.5=3520$Hz$. Using the same note, we can look at all
the fifths above it, where now the multiple is 1.5 instead of 2, so the n'th fifth
above A0 will have a frequency that is $1.5^n$ times greater. If you consider
the 12th fifth above A0, you get a note with a frequency multiple of $1.5^{12}=129.7$,
which is pretty close to the 7th octave,
in fact the difference between $129.7$ and $128$ is only 1.35%.
This means that after 12 fifths you pretty much get back to the same note.
So if you are building a music theory, and are fixated on fifths as the
defining multiple, and if you are assuming that 12 fifths lines up exactly with 7 octaves, then
that means you need 12 individual notes before things repeat.
This is (probably) the origin of the 12-note scale (called the diatonic scale).
The figure
below shows the frequency of the all the fifths (blue diamonds)
and octaves (red circles) above A0, as a function of frequency.
Since music is so geometrical, it would be better to make the above plot where the horizontal
shows which multiple (1st, 2nd, etc) as opposed to the value of the multiple itself. This can
be easily done by using a horizontal logarithmic scale (the logarithm of the multiple),
as seen in the next figure. This spreads the multipoles
out evenly, and you can see that the diamonds (fifths) are evenly spread out into multiples of
1.5, and the circles (octaves) are evenly spread out in multiples of 2.
The important thing here, as far as music theory goes, is that 7 octaves lines up pretty well
with 12 fifths. In fact, $2^7=128$ and $1.5^{12}=129.75$, equal to 1.35%.
The piano is a very nice instrument for learning music theory, as all the notes and relationship to
other notes are right there in front of you.
If you want to learn the history of the piano, you can read all about it in
Wikipedia. The short version is that it was
developed in the early 1700s when the harpsicord was the most widely used keyboard instrument.
On the harpsicord, when you played (pressed down on) any key, a mechanism plucked a string, giving it
that distinctive high-pitched "twang" sound,
whereas for a piano, playing any key caused a felt-tipped hammer to hit
the string (or as is on a modern piano, 1-3 strings),
allowing it to vibrate freely, resulting in a completely different tone.
By adding dampeners, you
could play it loud or soft (piano means "soft" in Italian, and the original name was
"pianoforte" which means "soft-loud"). The piano was too early for Bach, who hardly played
it, whereas by the end of the 1700s, composers such as Mozart, Haydn, Beethoven, etc played it
exclusively.
Most of the original harpsichords had a range of around 4 octaves, using just 60 keys,
so the earliest pianos also had only 4 octaves worth of keys.
As composers like Hayen and Mozart starting writing more and more music for pianos,
they found the 4 octave range to be limiting, thus increasing the pressure for more keys.
By the 18th century, pianos with 7 octaves were quite common, and composers such as
Liszt and Chopin made full use of all these keys. By the time Steinway asserted itself
as one of if not
the preeminent piano maker by the late 1800s, for various reasons pianos settled on
88 keys, with 7 full octaves of 12 keys per octave, and 2 partial octaves of 3 keys
in the lower range an only 1 key in the upper. Note that there are numerous piano
makers over the years that have extended the piano keyboard range.
For instance, Bosendorfer made
lots of 92 key pianos, adding 4 keys to the lower octave.
They even made a 97 key piano with
a full 12 key octave in the lowest range, and there are some pianos with even more
keys (Stuart & Sons has a piano with 102 keys).
The frequency of these 3 extra low keys in the Bosendorfer are pretty low,
and not much music is written for it, however a piano is a rather complex instrument,
and to some extent all the keys resonate with each other, so having more keys in the
lower range that you don't play will still make the piano sound "fuller", providing it's
tuned corrected! But that's another story.
On the piano, each key plays a note with it's own unique frequency.
As discussed above, there are 12 notes per octave, and an octave is defined as x2 in frequency.
That is, any two notes with frequency $f$ and $f'$ are octaves apart if $f'=2f$.
Now lets figure out the frequencies of the 12 notes between $f$ and $f'$. Let's start
with the first note $f_1$ (same as $f$). Then we will have 12 unique notes, $f_1,f_2,...f_{12}$
before we get to the octave note $f'$. You can see this on the piano: start with any note,
whether a white or black key, and count the number of notes (black and white) before you get
back to the key that restarts the pattern.
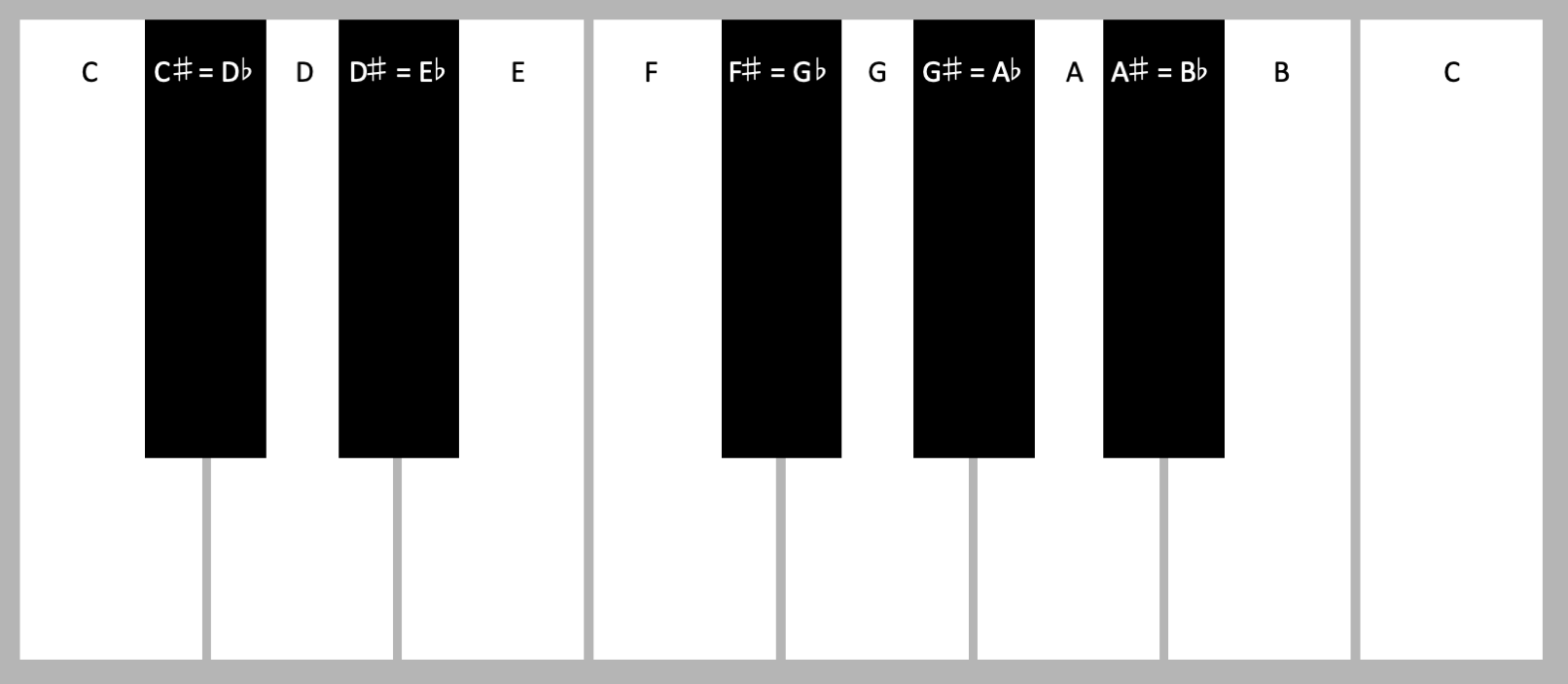
For example, let's pick any C in the middle of the
keyboard, as in the figure below:
There are 2 interesting things to note here that form the basics of music theory:
Now, let's consider the frequencies of the notes within the octave.
Since octaves are multiplicative, it would make sense to have each note a fixed
ratio above the previous note (and below the next note) in frequency. So we would
want $f(C\sharp) = \alpha f(C)$ where $\alpha$ is some number close to but greater
than 1. Moving up the octave, we would want $f(D)=\alpha f(C\sharp) = \alpha^2 f(C)$.
You can probably see where this is going, because when we get to the final note
in the octave, $B$, we would have $f(B)=\alpha^{11}f(C)$. And this means that
the frequency of the note $C'$ that is an octave above our starting $C$ will be
given by $f(C')=\alpha^{12}f(C)$. But we already know that $f(C')=2f(C)$ since
$C'$ is one octave above $C$. This tells us that
$$\alpha^{12}=2\nonumber$$
or
$$\alpha = 2^{1/12}=1.05946309...\label{deltaf}$$
where the notation $2^{1/12}$ means "twelth root of 2", or in other words a number
($1.05946309...$) that when
mulitplied by itself 12 times, gives 2.
This means that each half tone constitutes an increase
in frequency of approximatley 5.9% greater than the note below it.
Now that we know the ratio of all the notes on the piano, we only have to choose the
frequency of any one note and the rest are set using the transcendental number $2^{1/12}$.
What people typically do nowadays (and have for at least 100 years) is to take the note
$A4$, which is the 5th $A$ on the piano, and assign it a frequency of $f(A4)=440$Hz.
This means that the bottom note on the piano, $A0$, would have a frequency of $f(A0)=27.5Hz$
(so that $f(A4)=2^4f(A0)$,
and the top note would have a frequency $f(C8)=2^{87/12}f(A0)=4186$Hz.
This is a remarkable range: $27.5-4186$Hz. The violin and harp come close to matching the
piano in the high registers, but not the low. The and other than the organ and harp,
not many other instruments come close in
frequency range, except the violin and harp as can be seen in the following figure.
However, we've just shown that in hearing notes it's the difference in octave, and not the actual
difference in frequency, that matters. So to get a real measure of the range of the various
instruments, we should show the range of octaves instead of frequency. This is shown in the
figure below where the horizontal range is the number of octaves above the lowest frequency of any
instrument, the $16$Hz of the Pipe Organ. The plot is sorted so that the instruments with the
greatest range in octaves are at the top, and the lowest range at the bottom, regardless of where
that range falls (relative to 16Hz).
As you can see in the figure, the Pipe Organ, Harp, and Piano have by far the
most range in octaves, followed by the Harpsichord, Violin, Guitar, and Cello.
This probably has to do with the fact that one often sees concertos
(orchestra and solo instrument) with a piano, violin, cello, and even guitar: probably the fact that these
instruments have tremendous range plays a role. That we don't see more concertos with the
Pipe Organ
probably has to do with the overwhelming sound of the organ (drowning out the orchestra) and that
such organs are usually fixed in location. There are some concertos with the Harpsichord, but the
Piano is much richer an instrument.
As shown above, the frequency of successive notes on a piano
(and any other instrument for that matter) increases by a fixed ratio as you go up
the keyboard. This means that the frequency difference between any 2 half tones
is not constant, but instead is larger for notes in the higher octaves than it is for
notes in the lower half.
For instance, in the first octave, the frequencies for $C$ and $C\sharp$ are
$f(C1)=32.7$Hz and $f(C1\sharp)=34.65$Hz. The difference is given by
$\delta f=34.65-32.7=1.84$Hz. In the 6th octave, where $f(C6)=1046.5$Hz
and $f(C6\sharp)=1108.7$Hz, $\delta f=62.2$Hz.
Now imagine you have a piano, and you want to tune it, but you have a piano that
is not exactly a standard \$200,000 Steinway concert grand so you want the notes to
have the right frequency, but it's not critical to get it exactly right. So you want
to be have some measure of "how close". Imagine you use the frequency difference
as a measure of "how close", and say that you want the difference to be less than say
1 Hz. Then for the lower notes, that particular 1 Hz will be a much bigger fraction
of the total difference between notes than it will be for the higher frequency notes.
For instance, for $C$ and $C\sharp$ in the first octave, 1 Hz is $1/1.84=.54$, so
it's 54% of the interval, whereas in the 6th octave 1 Hz is $1/62.2=0.016$, or 1.6% of
the interval. This is not a good way to measure "how close" unless you want to change
the frequency difference you are shooting for as a function of which note you are
trying to tune. But then that's not so hard, you just have to have a sliding scale!
This sliding scale is what people use, and it's characterized by the term "cent".
Temperaments:
All rights reserved. No part of this publication may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the publisher, except in the case of brief quotations embodied in critical reviews and certain other noncommercial uses permitted by copyright law.
Reflection at a Boundary
Octaves
Fifths
The Piano
Back to top
Now let's calculate the frequencies of all the notes in a system based on octaves. The octave
is defined as by a x2 frequency range, so if you start with a note with (for example) frequency
$f=100$Hz, then the note $f'$ 1 octave above will have a frequency x2 higher, or
$f'=200$Hz. And the note $f''$ that is an octave above $f'$ will have a frequency
$f''=2f'=400$Hz. This means that each octave spans twice the frequency range of the
previous octave, so notes in octave 1 will span some range and notes in octave 5
will span a frequency range 16x higher than the range in octave 1.
Why is this the case? It has to do with the fundamentals of hearing. We are just
wired to hear this way!
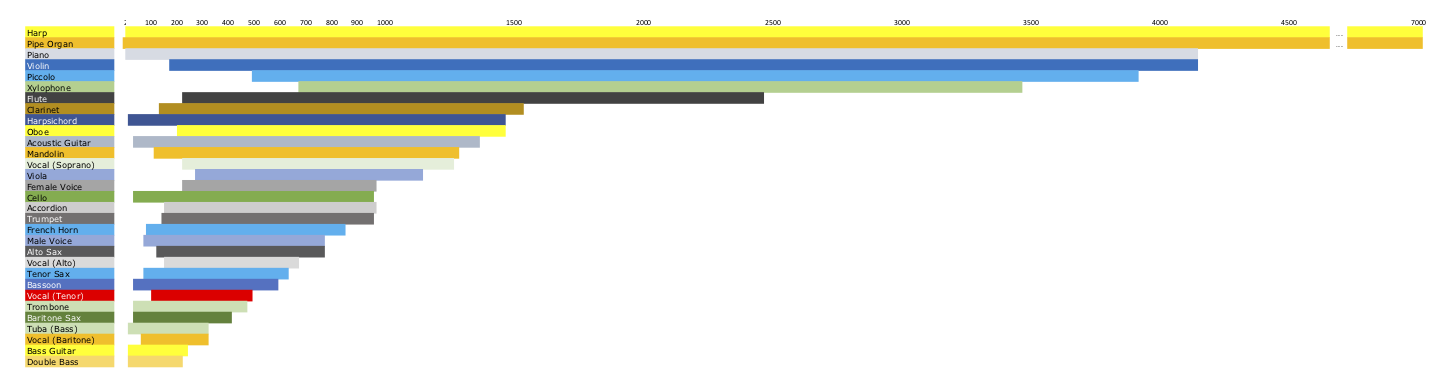Horizontal is in Hz
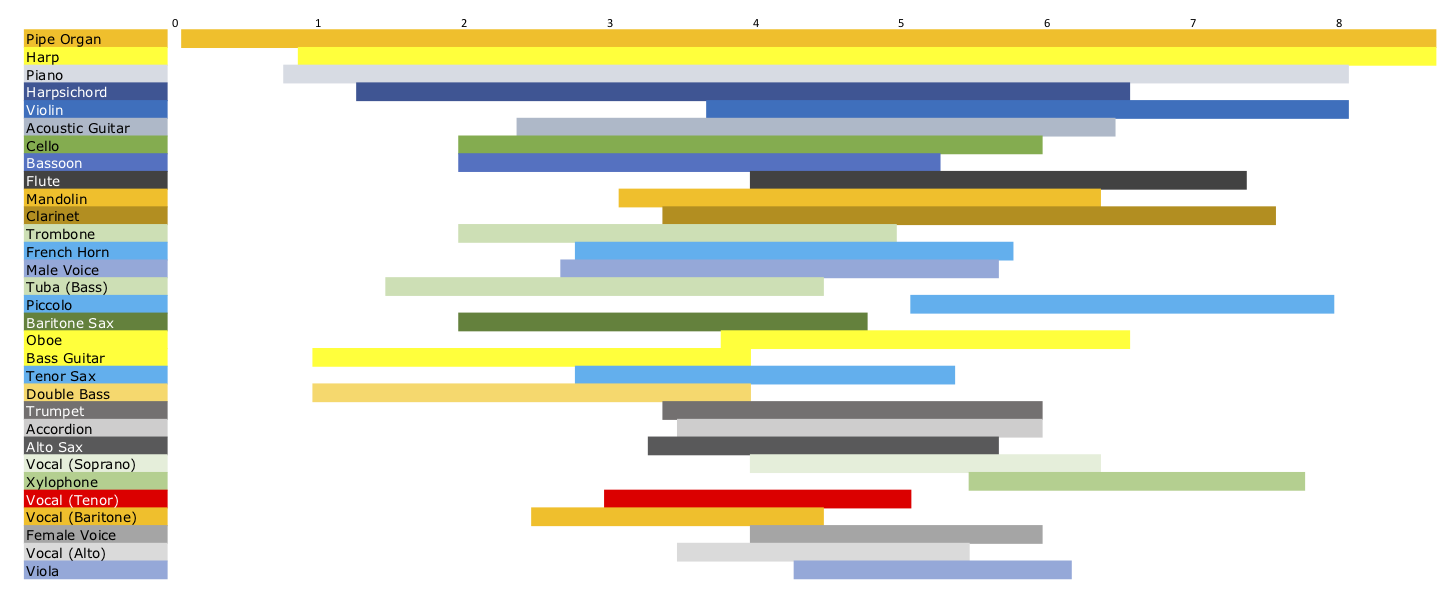Horizontal is octaves above 16Hz
Cents
The ratio of adjacent notes is given by $f_{n+1}=2^{1/12}f_n$. This
ensures that octaves are ratios of $f_{octave n}=2*f_{octave n}$
Copyright © 2019 by Drew Baden