I first saw this problem on the YouTube channel 1blue3brown. As in the figure below, it involves 2 masses of unequal mass. The small one is $m$ and the large one is $M$, they are both on a frictionless surface. $m$ is between $M$ and a wall. The mass $m$ has velocity $u$ and the mass $M$ has velocity $v$, and initial condition are $u_0=0$ and $v_0 \ne 0$, and is moving to the left. Let's the define the velocities as being positive to the left, towards the wall. Each $m$-$M$ collision is completely elastic, as is $m$ with the wall.

The initial condition has $M$ moving with velocity $v_0$ to the left. At the first collision with $m$, $M$ slows down a little and $m$ picks up some velocity going to the left, towards the wall. It hits the wall, reverses velocity, and heads towards $M$. When they collide, $M$ slows down even more, $m$ picks up a bit more velocity, and heads back towards the wall. As time goes on, $M$ slows down, gets closer to the wall, $m$ speeds up, and starts bouncing back and forth faster and faster as the distance between $M$ and the wall decreases. At some point, $m$ takes all the momentum out of $M$, which causes $M$ to stop. But $m$ is still bouncing, so it then begins to push $M$ to the right. $M$ picks up speed, and the distance to the wall increases. $M$ will never quite get back to the initial momentum (but heading to the right) because $m$ will never slow down to exactly $u=0$. The two masses no longer collide once it gets to the point where $v\gt u$ heading to the right and $M$ outdistances $m$. So from the point of view of $M$, it makes an elastic collision with the wall and bounces off heading to the right.

The really interesting thing here is to count the number of times (call this $n$) that $m$ collides with either the wall, or $M$, as a function of the mass ratio $x\equiv m/M$. What we find is that for $x=100$, $n=31$. For $x=10^4$, $n=314$, for $x=10^6$, $n=3141$, and for $x=10^8$, $n=31415$. See the pattern? For $x = 10^{2k}$, the number of collisions $n$ sweeps through the first $k+1$ digits of $\pi$.

What we want to know (or at least, what I want to know), is what the number of collisions could possibly have to do with $\pi$, which involves circles!

First, in the simulation below, you can change the value for the mass ratio $x$ via the text window below, and the system will report the predicted number of collisions and the actual collisions when you run the simulation. The simulation will stop when both masses are moving to the right, with the larger mass moving faster than the slower one. The status of the simulation will be reported below the buttons (either "Running..." or "Done!"). Note that the simulation will stop when the velocity of $M$ is greater than $m$, and the mass $M$ is off the page. Since the velocity of $m$ gets rather large as $x$ gets small, then sometimes $M$ can go past the end of the simulation drawing. The simulation will keep running but you won't see the collisions, and the time between collisions will increase. To help with this problem, there's a button called "Rescale" next to the "Reset". Push that button and it changes the scale by a factor of 1/2 so that things are renormalized out of convenience.

One more thing: if you try setting the mass ratio to an extremely small number (like $10^{-6}$ or smaller), the simulation will still work, but it will be difficult to control.

Mass ratio:

Collisions: Predicted = Actual =

$m$$M$
Velocity

IDLE

To calculate the changes in the velocities after each $m$-$M$ collision, first define $u_b$ and $v_b$ as the velocities before the collision (with positive velocities to the left), and $u_a$ and $v_a$ as the velocities after. Then apply momentum and kinetic energy (KE) conservation: $$\begin{align} mu_b + Mv_b &= mu_a + Mv_a\nonumber\\ mu_b^2 + Mv_b^2 &= mu_a^2 + Mv_a^2\nonumber\\ \end{align}\nonumber$$ To make things easier, define $x\equiv m/M$, and rewrite the above as $$\begin{align} xu_b + v_b &= xu_a + v_a\label{eqp}\\ xu_b^2 + v_b^2 &= xu_a^2 + v_a^2\label{eqKE}\end{align}$$ Rewrite equation $\ref{eqp}$ as $$x(u_b-u_a) = v_a-v_b\label{eqp1}$$ and equation $\ref{eqKE}$ as $$\begin{align} x(u_b^2-u_a^2) &= v_a^2-v_b^2\nonumber\\ x(u_b-u_a)(u_b+u_a) &= (v_a-v_b)(v_a+v_b)\label{eqKE1} \end{align}\nonumber$$

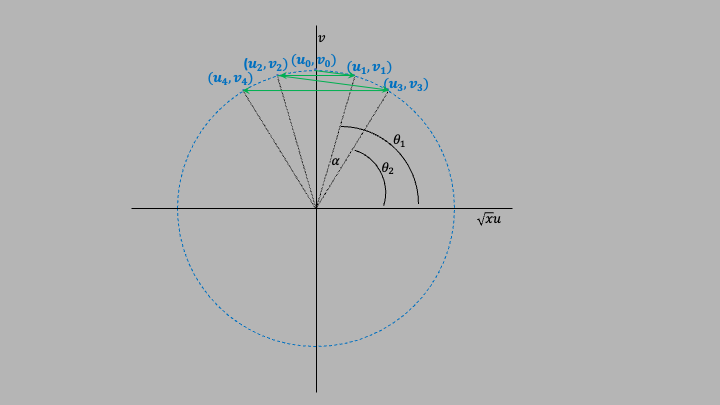
Then divide $\ref{eqKE1}$ by $\ref{eqp1}$ to get $$u_a+u_b = v_a+v_b\nonumber$$ or equivalently: $$v_a-u_a = u_b-v_b\label{eq3}$$ This gives us 2 linear equations to solve: $$\begin{align} xu_a + v_a &= xu_b + v_b\nonumber\\ -u_a +v_a&= u_b-v_b\nonumber\\ \end{align}\nonumber$$ Solving for $u_a$ and $v_a$ gives $$\begin{align} u_a &= \frac{2v_b-(1-x)u_b}{1+x}\nonumber\\ v_a &= \frac{(1-x)v_b + 2xu_b}{1+x}\nonumber\\ \end{align}\nonumber$$ To make things easier, define $$a\equiv 1+x\label{eqa}$$ $$b\equiv 1-x\label{eqb}$$ The equations for the final velocities $u_b$ and $v_b$ after each $m$-$M$ collision are then $$\begin{align} u_a &= \frac{2v_b-bu_b}{a}\nonumber\\ v_a &= \frac{bv_b+2xu_b}{a}\nonumber\\ \end{align}\nonumber$$ For collisions with the wall, the equations are simple: $$\begin{align} u_a &= -u_b\nonumber\\ v_a &= v_b\nonumber\\ \end{align}\nonumber$$ Note that if we use $k$ to represent the kth collision, then $k=1$ will be the first $m$-$M$ collision, $k=2$ will be the 1st $m$-Wall collision, $k=3$ the next $m$-$M$ collision, and so forth. So all of the odd values of $k$, we have $m$-$M$ collisions, and for the even values, we have $m$-Wall collisions. So for the $k$ odd terms, we have: $$\begin{align} u_{k+1} &= \frac{2v_k-bu_k}{a}\label{equa}\\ v_{k+1} &= \frac{bv_k+2xu_k}{a}\label{eqva}\\ \end{align}\nonumber$$ and for $k$ even: $$\begin{align} u_{k+1} &= -u_k\nonumber\\ v_{k+1} &= v_k\nonumber\\ \end{align}\nonumber$$ Next, note that even though the total momentum of $m$ and $M$ is not conserved after the $m$-Wall collisions, the kinetic energy is, and will be given by: $$KE = \half Mv_0^2 = \half mu^2 + \half Mv^2\label{eqKE0}$$ or dividing by $M/2$ gives $$xu^2 + v^2 = v_0^2\label{eqKE2}$$ The sequence of velocities is important. We start with $u_0=0$ and a nonzero value for $v_0$, then go to the first ($k=1$) $m$-$M$ collision. $u_1$ increases from 0 moving in the positive direction (towards the wall), and $v_1$ reduces slightly. If we were to plot the values $u\sqrt{x}$ vs $v$, it will form on the circle defined by equation $\ref{eqKE2}$, however it will not sweep out the circle! This is because in between the odd $m$-$M$ collisions we will have the even $m$-Wall collisions where $u$ will switch sign from positive (towards the wall) to negative (away from the wall). This is shown in the diagram below for the first 4 collisions. The green arrow lines show the sequence, so you see that the even $k$ collisions ($m$-Wall) green lines are horizontal.

Also shown in the diagram above are the first 2 angles $\theta_1$ and $\theta_2$ that label the coordinates $(u\sqrt{x},v)$, and the angle $\alpha$ between the first 2 $m$-$M$ collisions ($\alpha = \theta_1-\theta_2$). Let's calculate the $\alpha$ angles. First, let $n$ be the $m$-$M$ collisions. The index $k$ runs from 1 to the final number of collisions, $N$, so there will be half as many $n$ values as $k$ values. Each $n$ will correspond to the odd values for $k$, and we can construct the formula for $u_{n+1}$ and $v_{n+1}$ using equations $\ref{equa}$ and $\ref{eqva}$ using the fact that inbetween successive $n$ values, $v$ stays the same but $u$ reverses sign: $$\begin{align} u_{n+1} &= \frac{2v_n+bu_n}{a}\label{equn}\\ v_{n+1} &= \frac{bv_n-2xu_n}{a}\label{eqvn}\\ \end{align}\nonumber$$ Now we are ready to calculate the $\alpha$ angles for all successive $n$ data points using $$\tan\theta=\frac{v}{u\sqrt{x}}\nonumber$$ which means $$\alpha_{n+1}=\theta_n-\theta_{n+1}=\tan^{-1}\frac{v_{n}}{u_{n}\sqrt{x}}-\tan^{-1}\frac{v_{n+1}}{u_{n+1}\sqrt{x}}\nonumber$$ We can simplify using the identity $$\tan^{-1}a - \tan^{-1}b=\tan^-1\frac{a-b}{1+ab}\nonumber$$ which gives $$\tan\alpha_{n+1}=\frac {\frac{v_{n}}{u_{n}\sqrt{x}}-\frac{v_{n+1}}{u_{n+1}\sqrt{x}}} {1+\frac{v_{n}}{u_{n}\sqrt{x}}\frac{v_{n+1}}{u_{n+1}\sqrt{x}}}\nonumber$$ which after some algebra simplifes to $$\tan\alpha_{n+1}=\sqrt{x}\frac{v_nu_{n+1}-u_nv_{n+1}}{v_nv_{n+1}+xu_nu_{n+1}}\nonumber$$ Next we subtitute for $u_{n+1}$ and $v_{n+1}$ using equation $\ref{equn}$ and $\ref{eqvn}$ and use equation $\ref{eqKE0}$ to get $$\tan\alpha_{n+1} = \frac{2\sqrt{x}}{1-x}$$ This is pretty amazing, because it says

As $x\to 0$, $\alpha\to 0$ so we can use the approximation $\tan\alpha\to\alpha$ which gives the result $$\alpha \equiv \delta\theta = 2\sqrt{x}\label{eqdelta}$$ As discussed above, the system starts out at the top of the circle: $u_0 = 0$ and $v=v_0>0$ moving to the left. Collisions stop when the system gets to the bottom of the circle: $u_0 ~ 0$ and $v=-v_0$ moving to the right, away from the wall. So the dynamics map onto the circle once. The number of angles that can fit on the circle will be given by $$\begin{align} N &= \frac{2\pi}{\alpha}\nonumber\\ &= 2\pi \cdot \frac{1-x}{2\sqrt{x}}\to \frac{\pi}{\sqrt{x}}\nonumber\end{align}\nonumber$$ as $x\to 0$. Of course, $N$ is an integer so the number of collisions will be given by $$N = int(\pi/\sqrt{x})\label{eqf}$$ where $int()$ is whatever floating point to integer you use (int, floor, etc) that truncates the fraction.
Last updated Dec 1, 2022 Drew Baden

All rights reserved. No part of this publication may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the publisher, except in the case of brief quotations embodied in critical reviews and certain other noncommercial uses permitted by copyright law.