Phys410 - Classical Mechanics
University of Maryland, College Park
Fall 2012, Professor: Ted Jacobson
Homework
Problems from Taylor,
Classical Mechanics
HW0 - due
at beginning of class, Tuesday 9/04/12
HW12
- pdf file - due at beginning of class, Tuesday
12/12/12
HW11 - pdf
file - due at beginning of class, Tuesday
12/04/12
HW10 - due at beginning
of class, Tuesday 11/20/12
13.12 (bead on spinning
rod)
13.13 (particle on cylinder
with restoring force)
S10.1 (Hamiltonian for non-relativistic particle, and cyclotron motion)
(a) Find the Hamiltonian for a non-relativistic free particle of
mass m.
(b) Now include an external electromagnetic field, and show
that for a charge e the Hamiltonian is H = (p - eA)2/2m+
eV,
where V and A are the
scalar and vector potentials. Note that in a magnetic field (with no
scalar potential), the Hamiltonian is
given by H = 1/2 mv^2, the kinetic energy
(but v must be regarded as a function of the momentum, the position,
and the vector potential).
(c) Suppose there is just a uniform magnetic field in the z
direction, which can be derived from the vector potential A = Bx yhat.
Show that the orbits in the xy plane are circles with angular
velocity w_0, where w_0 = eB/m is the nonrelativistic
cyclotron frequency.
In your analysis you may for convenience set the conserved
quantity p_y to zero (after finding Hamilton's equations), since
it just determines
the x coordinate of the center of the circular orbit (see
Problem S4.2). Where does the freedom of the y coordinate of the
center of the orbit arise
in solving the equations?
(d) Express the energy as a function
of the radius of the orbit, w_0, and m.
S10.2 (Hamiltonian for
relativistic particle, and cyclotron motion)
The action for a relativistic free particle is -m∫
dt (1-v2)1/2,
where v = dx/dt, i.e. the Lagrangian is
L = -m (1-v2)1/2.
(a) Find the momentum p
conjugate to x.
(b) Show that p2
+ m2 = γ2m2,
where γ = (1-v2)-1/2.
(c) Show that the Hamiltonian is H = (p2
+ m2)1/2
(in units with c = 1).
(d) Now include an external electromagnetic field, and show
that for a charge e the relativistic Hamiltonian is H =
[(p
- eA)2
+ m2]1/2+
eV,
where V and A are the
scalar and vector potentials. Note that in a magnetic field (with no
scalar potential), the Hamiltonian is given by H = γm.
(e) Suppose there is a uniform magnetic field in the z direction,
which can be derived from the vector potential A = Bx yhat.
Show that the orbits in the xy plane are circles with angular
velocity w = w_0/γ, where w_0 = eB/m is the
nonrelativistic cyclotron frequency.
In your analysis you may for convenience set the conserved
quantity p_y to zero (after finding Hamilton's equations), since
it just determines
the x coordinate of the center of the circular orbit (as in the
nonrelativistic case, Problem S4.2).
(f) Eliminate the velocity using v = Rw, and show that w =
w_0/(1+R^2 w_0^2)^1/2. Note that this ensures that the speed is
never greater than
the speed of light, and that as the radius grows the speed
approaches the speed of light.
(g) Express the energy as a function
of the radius of the orbit, w_0, and m. Show that
in the non-relativistic limit you recover S10.1(d).
S10.3 (Gravitational redshift)
Consider two light pulses sent radially outward from radius r_1
to radius r_2 in the Schwarzschild spacetime,
ds^2 = F (r) dt^2 − 1/F(r) dr^2/c^2 − (r^2/c^2)(dθ^2 + sin^2 θ
dφ^2),
where F(r) = 1 − r_g/r, and r_g =
2GM/c^2 is the Schwarzschild radius. Suppose
the emission events are separated by
a Schwarzschild coordinate time interval ∆t. (a) What is the Schwarzschild
coordinate time interval between the arrival of the two pulses
at r_2?
(b) What is the proper time ∆s_1 between the emission of the two
pulses at r_1? (c) What is the proper
time ∆s_2 between the reception of the
two pulses at r_2? (d) Suppose a photon is emitted radially from
r_1 with frequency w_1 measured by a static observer at r_1.
When the photon arrives
at r_2, what will be its frequency as measured by a static
observer at r_2? (e) As r_1 approaches the Schwarzschild
radius, what happens to the frequency
w_2, if w_1 is fixed? [Suggestions:
(i) It may help to visualize this using a spacetime diagram,
e.g. showing constant r lines as vertical and light pulses as
diagonal. (ii) To answer part (a) you should use the
t-translation symmetry of this spacetime.]
S10.4 (Motion
in a gravitational wave)
The line element describing a plane gravitational wave of frequency
ω propagating in the x direction can be written (in c = 1 units) as
ds^2 = dt^2 − dx^2 − [1 + h sin[ω(t−x)] dy^2 − [1 − h sin[ω(t−x)]
dz^2.
(a) Show that if a test mass governed by the action −m ∫ ds is
initially “at rest” in these coordinates (i.e. if dx/dt = dy/dt =
dz/dt = 0 initially),
then it remains so for all times.
(b) Show that if a ring of independent test masses in the x = 0
plane is at rest with respect to these coordinates at t = 0, then
the physical shape
of the ring, defined by the invariant distance between points on the
ring at a constant value of the t coordinate, oscillates between two
ellipses with
perpendicular major axes.
HW9 - due at beginning of
class, Tuesday 11/13/12
15.46 (approaching and receding Doppler factors)
15.48 (transverse Doppler effect)
15.87 (pion decay to photons:
pion velocity and photon angle)
(Suggestion: The velocity of the CM frame can be obtained
from the total momentum divided by the total energy.)
15.90 (pair creation off
nucleus) Do part (a) by showing that the sum of two
future timelike 4-vectors cannot be lightlike.
15.92 (pion decay to lepton
and neutrino)
(Suggestion: You are only being asked for the speed, so
try to get the gamma factor directly, without evaluating any
energy or momentum
Express the neutrino 4-momentum in terms of the pion and muon
4-momenta, take its scalar product with itself, and impose
the mass shell conditions.)
S9.1 (no vacuum Cerenkov
radiation) Show that the reaction e -> e + gamma
cannot satisfy both energy and momentum conservation.
You could do this at least three different ways: by (i) writing
out energy and momentum conservation and applying the mass
relation
in a general frame, (ii) doing the analysis in the rest frame of
the initial electron, or (iii) using 4-vectors and proving the
result for problem 15.53.
S9.2 (cosmic gamma ray cutoff)
Although gamma rays of energies up to 1020 eV are
created by ultra high energy cosmic rays throughout the
universe, they cannot travel all the way to the earth, because
on the way they collide with other photons and disappear,
creating electron-positron
pairs. The reaction is gamma1 + gamma2
-> e+ + e-. (a) If the two
photons collide head-on, show that for a given energy
E2 of photon 2, the minimum
energy E1
of photon 1 required to create the pair is E1 = me2/E2.
(b) Evaluate this energy (in eV) assuming E2
is the energy of (i) a typical cosmic microwave
background photon, 3K = 0.0003 eV, or (ii) a mid-infrared photon
of energy 25 meV. (The actual energy cutoff of
cosmic ray photons originating from more
than around 100 million light years comes from annihilation on this
infrared background radiation.)
HW8 - due at beginning of class,
Tuesday 11/06/12
15.7 (muon
lifetime in cosmic ray showers)
15.12 (Lorentz
contraction)
Answer only (b) How long is the pipe as "seen" (better word
would be "reckoned") by the pions, and how long does it take to
pass the pions?
Answer the question about the length two ways: i) Using the time
for the pipe to pass, together with the speed of the pipe; ii)
Using the length
contraction formula (15.15). This should explain how length
contraction is the "flip side" of time dilation.
15.56 (rest energy in chemical
reaction)
15.57 (rest energy in nuclear
reaction)
15.58 (rest energy vs. kinetic
energy)
15.71 (collision energy to
create a particle)
See the sections in the textbook on CM frame and Threshold
energies, p. 645. And/or, use Hint: The E^2 - p^2
c^2 is the same in all inertial frames,
where E is the total energy of all particles and p is the
magnitude of the total momentum.
15.75 (parent particle
reconstruction)
S8.1 (relativistic longitudinal Doppler effect)
This problem refers to the situation and notation with
observers O1 and O2 described in the latex notes.
(a) Explain why the ratio t1/t0 is the Doppler factor
for light, i.e. the ratio of received frequency to
transmitted frequency for light sent from O1 to O2.
(b) Show that t1/t0 = √t1/t2. (c)
The the expression of t1 and t2 in terms of ∆x and ∆t to
show that the Doppler factor is √(1-v/c)/(1+v/c). (d)
For v << c
it is useful to use an approximation. Expand the Doppler
factor to linear order in v/c to find this
approximation.
HW7 - due at beginning of class,
Tuesday 10/30/12
11.32 (CO2 vibrations) Do the eigenvalue and eigenvector
calculations by hand.
(Suggestion: Once you
have worked out the equations of motion, adopt units with k = m
= 1.)
Add to part (b): Which mode has the higher frequency? Try to
explain "why", without reference to equations.
Add parts: (d) Show that the ratio of the two frequencies is
√11/3, taking into account
that the ratio of carbon to oxygen mass is 3/4. Show that the
observed frequency ratio is smaller by
about 12%.
(See www.phy.davidson.edu/StuHome/jimn/CO2/Pages/CO2Theory.htm
for information on carbon dioxide vibrations.*)
(e) Try to give a physical reason (or reasons) why the observed
ratio is smaller than that in our simple model.
I don’t think the difference between quantum and classical
mechanics is the most important issue in this case.
(Hint: Think about the
physical nature of the “springs” in the molecule and how they
differ from those in our model.)
*The frequencies are given on this web page in units of cm−1.
This refers to the inverse wavelength of the photons that are
emitted in
transitions between the vibrational levels. For an oscillator of
frequency ω
the quantized energy levels have energies (n+1/2)ℏω.
The energy difference between two adjacent levels is therefore
ℏω, so the emitted photon frequencies are ω.
The inverse wavelength
is thus proportional to ω,
the frequency of the oscillator.
S7.1 (masses suspended by
springs)
Consider a mass m suspended by a spring with spring constant k
from another mass m which is suspended from a fixed support by
another
spring with spring constant k. Let y_1 and y_2 denote the
displacements from their equilibrium positions of the top and
bottom masses
respectively, with the downward direction taken as positive.
Consider only vertical motion. (a) Write the Lagrangian for the
system, and find
the equations of motion. (Note the
equilibrium spring forces balance the gravitational forces,
which therefore drop out of the problem.)
(b) Determine (by hand) the normal mode frequencies and
displacement ratios y_2/y_1. (To check your result: The squared
frequencies are
(3± √5)/2 and the displacement ratios are y_2/y_1 = (1
-/+ √5)/2.) (c) Describe and indicate with arrows the nature of
the two normal mode motions,
showing both direction and approximate relative displacement of
each mass. Label with the frequency of each mode. Which is the
higher one?
Try to explain "why", without reference
to equations.
S7.2 (physical pendulum
hanging from a string)
Consider a
uniform rod of mass M and length R hanging by its end from a
massless string of length l.
(a) Write the Lagrangian using the angles of the string and rod
as generalized coordinates, and expand it to quadratic order in
the angles.
(b) Find the frequencies of the normal mode oscillations for
motion in a plane.
(c) Evaluate the frequencies in three cases: l=R, l >> R,
and l << R.
(Notes: (i) When you
write the kinetic energy, decompose it into the center of mass
motion and the motion relative to the
center of mass, and for the latter make use of the moment of
inertia relative to the center of mass (not relative to the end
of the rod).
(ii) I suggest you adopt units with M=R=g=1 for part (b). (iii)
Answers for part (c): case 1:
3.1√g/R, 0.8√g/R;
case 2: √6g/R, √g/l; case 3: √3g/2R,
2√g/l.)
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
OPTIONAL EXTRA CREDIT PROBLEM: not difficult, but nice. If you
choose to do this problem it will be graded and added to your
worst previous
homework score, normalized as 25/100. E.g., if you previously
got 60/100, that will be adjusted to 85/100 (totals greater than
100/100 are allowed).
S7.3 (charged particle on a cylinder in a transverse magnetic
field)
A particle of charge q and mass m is confined to a cylinder of
radius R, centered on the z axis, in the presence of
a uniform magnetic field in the x direction, B = B xhat.
Use cylindrical coordinates (rho, phi, z) for the position of the
charge.
(a) Show that A = By zhat is a vector potential for
this magnetic field.
(b) Write the Lagrangian for the charged particle.
(c) Now rewrite the Lagrangian in units with $m=R=qB=1$ (check that
this is allowed), and find an expression for the energy of the
particle.
(d) Show that the canonical momentum p_z conjugate to z is
conserved. (What symmetry is responsible for this?)
(e) Using the Lagrangian method, find the force of constraint that
holds the particle on the cylinder as a function of its position and
velocity.
(f) Find the effective potential for a given value of p_z, and
carefully sketch or plot it (from -π to π) for the values p_z = 0,
1/2, 1.
(g) Describe the qualitatively different possible motions of the
charge for each of the three values of, p_z in part (f).
HW6 - due at beginning
of class, Tuesday 10/16/12
9.2 (artifical
gravity in rotating space station)
9.7 (derivative of vector in
rotating frame)
9.8 (direction of centrifugal
and Coriolis forces)
[Be sure to describe the components both tangent and normal to
the Earth's surface.]
9.11 (Lagrangian in rotating
frame and equations of motion) The textbook suggests to
do this problem using vector notation,
without coordinates. However in this case, with constant angular
velocity, it's not hard to use coordinates and it eliminates the
need for fancy footwork with vector identities. So, instead of
using vectors, I suggest you adopt Cartesian coordinates, with
the z axis along the angular velocity of the rotating frame. The
coordinates in the two frames are related by
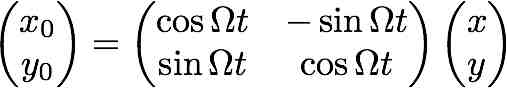 , so
, so 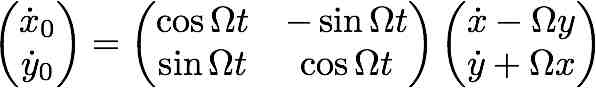 .
.
Once you get the three Lagrange equations, you can then show
they are equivalent to (9.34).
[Tip: The kinetic energy term is invariant under a
rotation of the velocity vector!]
[You could also do it with cylindrical coordinates, in
with phi_0 = phi + Omega t.]
9.22 (Larmor precession via
rotating frame trick)
9.26 (approximate trajectory
of falling particle on spinning earth)
S6.1 (tides for a constant
central force) It is often said that the ocean tides
can be traced to the fact that the moon's
gravitational force gets weaker with distance. But in fact we
would have tides even if the moon's force on the earth were
independent of distance, because of the direction dependence.
To see how this works explicitly, let's assume that the force
the moon
exerts is central and everywhere has the same magnitude as the
true gravitational force of the moon has at the center of the
earth.
That is, F =
-(GMm/d_0^2) dhat, where
M is the mass of the moon, m is the mass of the particle it is
acting on, d_0 is the distance from
he center of the moon to the center of the earth, and dhat is a unit vector
pointing from the moon to the particle. For this problem, you
will go through the same steps as in the textbook, but for the
modified force field. (a) Write down the tidal force field (as
in Eq. 9.12).
(b) Sketch the tidal force field at the surface of the earth (as
in Fig. 9.4). (c) Find the tidal potential (as in Eq. 9.13). (d)
Find the height
difference between high and low tides in the idealized model (as
in Eq. 9.18). How does your result compare with the true result
(9.18)?
HW5 - due at beginning of
class, Tuesday 10/09/12
8.2 (two bodies in an
external field) Add parts: (c) If the external field is
not uniform then the center of mass motion
no longer separates completely from the relative motion. For
instance, this is the case for the earth-moon system in
the presence of the sun. Write the Lagrangian of the earth-moon
system using the earth-moon center of mass and
relative position vector as your coordinates. Explain which
terms spoil the separation of the center of mass and relative
motions.
(d) Look at en.wikipedia.ord/Lunar_theory#Newton to see how
Newton analyzed this using the vector sum of forces.
8.3 (two masses, spring and
gravity) Note:
The solution in the book is only valid if the table is removed
at t=0.
You can assume this is the case, to simplify the problem.
S5.0 (spinning rod with finite inertia) Heretofore we
considered a rod, forced to spin at a fixed angular velocity,
and with a
bead constrained to slide along the rod. In that problem,
neither energy nor angular momentum are conserved. Now let's
change the problem and let the rod have finite moment of inertia
I, and let it spin freely on a frictionless axis, so that energy
and angular momentum are conserved. (a) Write the Lagrangian of
the rod + bead system, using for generalized coordinates
the angular position of the rod and the radial position of the
bead. Let the moment of inertia of the rod be I. (b) Write the
total energy for a fixed angular momentum in terms of the radial
kinetic energy of he bead plus an effective potential, and
sketch the effective potential. (c) Suppose the rod is spinning
and the bead begins with no radial velocity at some nonzero
radius. Describe qualitatively the subsequent motion of the
system, including what happens in the limit of infinitely late
time.
(d) Suppose the rod is spinning and the bead is moving towards
the center. Describe the three possible subsequent motions.
(Which of these occur is determined by the energy for a fixed
angular momentum.)
S5.1 (dark matter)
One of the first pieces of evidence for the existence of dark
matter was the "flat rotation curves" of galaxies, meaning the
fact that
at large radii the orbital velocity of stars (as measured by the
Doppler effect) approaches a constant, rather than falling off
with distance. (a) How does the velocity of a test body in a
circular Newtonian gravitational orbit around a central mass
scale
with the radius of the orbit? (b) Suppose the mass of a galaxy
is dominated by a spherical distribution of some kind of dark
matter
with a radial mass density profile rho(r). What form must the
function rho(r) take in order for the orbital velocities of
stars to be
independent of r? (c) For this rho(r), how does the mass M(r)
inside r, the force F(r) on a test mass, and the potential U(r)
of a
test mass depend upon r?
S5.2 (innermost stable
circular orbit in GR)
In general relativity there is a correction to the Newtonian
orbit around a central gravitating body that can be approximated
for weak fields and low velocities by an additional, attractive
1/r^3 term in the potential energy. The total effective
potential for a
body of mass m then has the form U =
-a/r + b/r^2 - d/r^3. Here a = GMm, where M is the mass of
the central body, assumed much
larger than m, b = l^2/(2m), where l is the angular momentum of
the orbiting mass, and d = b r_g, where r_g = 2GM/c^2 is the
"gravitational radius" or "Schwarzschild radius"
(for M = M_sun the gravitational radius is 3 km), and c is the speed
of light.
We can simplify the algebra by choosing units with GM = c = m = 1,
in which case a = 1, b = l^2/2, and d = l^2.
Assume you can use Newtonian dynamics.
(a) Show that no circular orbits exist for l < √12, and that for
each l > √12 there is one stable and one unstable circular orbit.
Sketch the form of the potential for these two cases, as well as for
the critical case l = √12.
(b) Find the lower limit of r for which a stable circular orbit
exists, and find the corresponding orbital energy and speed.
(The limiting orbit is marginally stable, and is called the ISCO,
"innermost stable circular orbit".) Use the above units in
your algebra, but once you have the result re-express the results in
terms of the dimensionful quantities GM, c, and m.
(The speed will not be small compared to c, so the Newtonian
treatment is not justified. Nevertheless, when properly
understood this result for r_ISCO agrees with the one in general
relativity.)
(c) Show that the unstable circular orbits exist between r = 6 and r
= 3, and find the energy of the orbit at r = 3.
S5.3 (precession of perihelion of
Mercury in GR)
Using your results from S5.2, consider an elliptical
perturbation of any stable circular orbit, and compute the radial
oscillation frequency
w_r in terms of the radius r. (Eliminate the explicit l
dependence by solving for l in terms of r). The precession rate is
w_p = w_phi - w_r,
where w_phi is the angular velocity. Assuming that r >> r_g,
find the leading order precession rate by expanding in the small
number r_g/r
(which is 2/r in our nice units). Restore the dimensionful
quantities using dimensional analysis, and evaluate the precession
rate for the
perihelion of Mercury, expressing the answer in seconds of arc per
century. For the radius use the semimajor axis of Mercury's
elliptical
orbit. [Tip: When
restoring the dimensionful quantities, you need only multiply by
appropriate powers of r_g/2 and c (which are both
equal to 1 in these units) so that you wind up with something that
has the dimensions of inverse time.] (Answer: w_p = 3r^(-5/2), 42"/century.)
HW4 - due at beginning of
class, Tuesday 10/02/12
7.49 (charged particle in
uniform magnetic field - polar gauge)
Add parts: (d) Show that the Hamiltonian is the kinetic energy.
(e) Find the conserved quantity conjugate to the angle
about the z-axis.
This is the z-component of angular
momentum, which is not the same as "mvr" (much as the linear
momentum is not mv.)
(f) For orbits of constant rho in the
xy plane, show that the energy is proportional to the
z-component of angular momentum,
and find
the coefficient of proportionality. (Be careful about the sign of the angular
momentum.)
(g) Show that dimensional analysis gives the same result
for the energy, up to a dimensionless constant
(which happens to be -1, and you could infer the sign from the
sign of the angular momentum). (h) Assuming the angular momentum
is
quantized in integer multiples of hbar, and using your classical
orbit results, find the quantized energies of a charge in a
planar orbit
in a uniform magnetic field. These
are the "Landau levels", except for a missing zero point energy.
(The quantum ground state has
zero angular momentum, but has a zero point energy hbar omega/2,
where omega is the orbital angular frequency.)
7.51 (pendulum with
constrained Cartesian coordinates)
S4.1 (ambiguity of Lagrangian)
We know that adding a total time derivative to the
Lagrangian only adds a constant to the action (for fixed
endpoints), so does not change the EL-equations.
This problem checks this explicitly, and is an exercise in
using partial derivatives and index notation.
(a) Show explicitly that if you add a
total time derivative (d/dt)f(x,t) to the Lagrangian
for a particle in one dimension, all the added terms in
Lagrange's equations cancel.
(b) Now allow for an arbitrary number of generalized coordinates
q^i, and do the same analysis. Make use of the Einstein
summation convention when appropriate.
S4.2 (charged particle in uniform magnetic field - Cartesian gauge)
A uniform magnetic field of strength B in the zhat direction is
described by a vector potential A = Bx yhat.
Unlike the potential in problem
7.49 for the same magnetic field, this one is not obviously
rotation invariant, but it is y-translation invariant. (a) Write
the Lagrangian for a particle of
mass m and charge q using this gauge, and find the equations of
motion. (b) From now on, choose units with m = qB = 1, and show
that the solutions
that have zero velocity in the z-direction are uniform circular
orbits with any center, with the same angular velocity you found
in problem 7.49.
(c) Show that the conserved quantity associated with the
y-translation symmetry is qB times the x-component of the center
of the circular orbit (!).
S4.3 (constraint for bead on
spinning rod) Consider problem 7.21 again. (a)
This time include the angular coordinate as a degree of freedom,
and write the Lagrangian with a constraint with Lagrange
multiplier that imposes the condition that the bead slides on a
rod that spins with
constant angular velocity omega. (b) Write the radial and
angular equations of motion. (c) Show that the Lagrange
multiplier term in the
angular equation of motion yields the torque on the bead.
S4.4 (catenary) A
flexible rope or chain hanging from two points forms a shape
called a "catenary", which is actually a hyperbolic cosine!
You can show this directly using the condition that the net
force on an infinitesimal segment of rope vanishes, but you can
also show it using
variational calculus. The calculation is nearly identical to the
problem of the soap film bounded by two rings that you already
solved on HW1,
but you need to impose the constraint that the rope has a given
fixed length b. Suppose the rope hangs from two points (x1,
y1) and (x2,
y2),
and
express the gravitational potential energy of of rope as an
integral involving the function x(y). Using the method of
Lagrange multipliers,
find the equation on x(y) implied by the fact that the potential
is a minimum for all variations of x(y) that keep the rope
length fixed.
Then re-express this as an equation on y(x), and show that the
solutions are given by y = c + a cosh[(x-x0)/a] (this should be
easy).
Compared to the soap film problem, there is an extra constant
here, c. This is necessary since there is one more condition to
be met:
besides the positions of the endpoints, the length of the rope
must be matched. [For this problem you need not find the
relation between a and b.
However, if you are curious, assume the two ends are at the same
height, choose the origin of coordinates so that x0=0 and
c=0, and use the length
constraint to show that b/2a = sinh(d/2a), where d is the
distance between the ends of the chain. This transcendental
equation determines a uniquely.]
HW3 - due at beginning of
class, Tuesday 9/25/12
7.20 (particle on a helix)
(Note: this could equally well be solved by writing down the
total mechanical energy and setting its time derivative to
zero.)
7.21 (bead on a spinning
horizontal rod) Let's add two interesting parts (b):
Suppose the rod has length L from the pivot to one end, and the
bead is released
with zero radial velocity at some initial radius r_0. In the
limit that r_0 goes to zero, what velocity does the bead have
when it reaches the end of the rod?
Give the components of the velocity along the rod and
perpendicular to the rod. Compare your result to what you would
expect from dimensional analysis.
(c) (i) Explain why neither the total mechanical
energy E nor the angular momentum J about the vertical axis
are conserved. (Hint:
What work and
torque are exerted on the bead?) (ii)
Explain why the Hamiltonian is a conserved quantity, and show
that it is equal to E - ω J, where E
and J are the
kinetic energy and angular momentum of the bead, and ω
is the angular velocity of the rod. (iii) Use this conservation law
to evaluate the kinetic energy
when the bead leaves the rod, and show that it agrees with what you
get using your results from part (b).
7.22 (pendulum in an
accelerating elevator) Change the second part: instead
of finding the equation of motion, show that the Lagrangian
itself is equal,
up to addition of a total time derivative, to the Lagrangian for
a non-accelerating pendulum with g replaced by g+a. (The total
time derivative does not
affect the equations of motion.) (Hint: You'll need to do an integration by
parts on a time derivative.)
7.37 (two masses connected by
a string through a hole in a table) Add part (e) What
does dimensional analysis (and a bit of physics logic) tell you
about the oscillation frequency in part (d)? (The problem
involves m, L (length of the string), g, and r_0.)
S3.1 (double pendulum)
(a) Write the Lagrangian for the double pendulum illustrated in
Fig. 7.3, assuming the masses are equal. (b) Expand the
Lagrangian to quadratic order in the amplitude of the angles,
dropping the higher order terms, and show that it takes the form
of two oscillators
coupled by a term quadratic in the velocities. (This describes
small oscillations about the equilibrium. Later we'll
find the normal modes.)
S3.2 (bead on a spinning
tilted rod) Reconsider Problem 7.21, where now
the rod makes an angle α with the vertical and spins about a
vertical
axis that goes through the bottom end of the rod. (a) Find the
Lagrangian for the bead on the rod in a uniform downward
gravitational field g, using
the distance s from bottom end of the rod as the generalized
coordinate. (b) Identify the effective potential, and sketch it
for no rotation and for a
nonzero angular velocity ω
of the rod. (c) For a generic value of ω, show that
there is one equilibrium point (other than s = 0),
and determine
whether it is stable or unstable.
S3.3 (least action for
free-fall) Consider a particle of mass m in a uniform
gravitational potential U(y) = mgy. Let y represent the height
of the particle,
and consider the action for vertical paths y(t) over the time
interval [-T,T], with y(-T) = 0 = y(T). The action for the path
y(t)=0 is zero, of course.
(a) Show that among the paths with uniform velocity on the way
up and the way down, the action is minimized for the one that
reaches the height
h = 1/2 g T^2, and show that the value of that minimum action is
-1/4 m g^2 T^3. (b) Show that the Newtonian path reaches same
same height as
you found in part (a) (a fluke?), and that the action for that
path is -1/3 m g^2 T^3. (c) Show that the m
g^2 T^3 factor follows from dimensional
analysis, and show that you can choose units with m=g=T=1 (if
you want to, you can make this choice at the beginning of the
problem).
HW2 - due at beginning of
class, Tuesday 9/18/12
6.6 (ds in various
settings)
6.16 (geodesics on a sphere)
6.19 (soap bubble)
Note: Assume y1 and y2
are both positive. [Hint: I found it simplest to
start with x(y) in the area functional,
but then to switch to y(x) after deriving the E-L equation.] [Note:
This problem contains considerable subtleties which you need
not enter into unless you feel like it. Namely, (i) there
is no solution of this form when the two rings are sufficiently
far apart
given their sizes, and (ii) not every solution to the E-L eqn is
a minimum area solution. In fact, for each ring configuration
admitting a minimum area surface connecting the rings, there is
a second surface at which the area functional is stationary
but not at a local minimum.]
7.3 (2d oscillator using
Lagrangian) Modify this problem as follows: (a) Write
the Lagrangian using polar coordinates.
(b) Find the equations of motion for phi and r. (c) define the
angular momentum by J = mr2phidot, and show that the
phi
E-L eqn implies that it is conserved. (d) Express the angular
part of the kinetic energy in terms of J and r (with no phi
dependence), and combine this with the oscillator potential to
obtain an "effective potential". Sketch the effective potential.
(e) Use energy conservation to express the radial acceleration
in terms of the effective potential. Find the circular orbit
(motion with rdot=0) for a given J, and describe the radial
motion for orbits with nonzero rdot and nonzero J.
(f) It is not obvious using these variables that the orbits are
closed. Start over and do the problem using Cartesian
coordinates,
and using that prove that the orbits form closed ellipses.
7.8 (CM
and relative motion of two bodies in 1d) Modify
this problem as follows: Instead of a spring, suppose the
potential
U is an arbitrary function of the separation of the two
particles, U(x), with x = x1 - x2. Replace
part (c) by "describe the resulting
dynamics". Add part (d) Now let the two masses be different.
Find the Lagrangian in terms of the center of mass position
X = (m1x1
+ m2x2)/M,
where
M
is the total mass M = m1 + m2, and x. The
so-called "reduced mass" μ = (m1m2)/M
will arise.
Express your result using this quantity. Show
that the center of mass moves at constant velocity, and that the
relative position
satisfies Newton's 2nd law with a mass μ.)
S2 (motion about equilibria
for bead on spinning hoop)
Example 7.7 discusses motion near equilibria of a bead on a
spinning hoop. It does so by expanding the equation of motion
about the equilibrium. Instead, let's expand the Lagrangian
about the equilibrium. Hence: the Lagrangian (7.68) can be
written
in the form L = 1/2 m R^2 qdot^2 - U(q), where I'm using q to
stand for theta. At an equilibrium point q_0 we have U'(q_0)=0.
(a) Make a Taylor expansion of U(q) about an equilibrium point
q_0. Keep terms out to quadratic order in the displacement from
equilbrium. (b) Stability is determined by the sign of the
quadratic term in U(q): if it's positive the motion is a stable
oscillation, if
it's negative the motion runs away exponentially. (i) Show that
below the critical angular velocity, the equilibrium at theta=0
is
stable and that at theta=π is unstable. (ii) Show that above the
critical angular velocity the equilibria at theta = 0 and π are
both unstable,
while the two new equilibrium points are stable.
HW1 - due at beginning of
class, Tuesday 9/11/12
Read the Chapter summaries of Chapters 1-5, and browse the
chapters. If you see anything you're not comfortable
with read that part of the chapter.
1.32 - (Newton's 3rd law
failure for magnetic forces between point charges)
read, but do not do, this problem
1.33 (Newton's 3rd law for
magnetic forces between closed current loops) This problem
is intriguing.
A couple of hints: (i) Evaluate grad1(1/s),
and
use
that
to
show
that
a part of the integral vanishes
because it's the line integral of a gradient around a closed loop. (ii) To establish the 3rd law,
show that
the force of loop 2 on loop 1 is proportional to ∫∫ (dr1. dr2) s/s3, which
obviously changes sign when
considering the force of loop 1 on loop 2.
4.4 (Particle on table
attached to string through hole)
4.24 (Gravitational potential
of an infinite rod) Do only parts (a) and (d). [Once
you find a potential that
gives the force, you don't need to check that the curl of the
force vanishes, since curl grad U = 0 for any U.]
4.36 (ball-pulley-mass gizmo)
4.38 (pendulum period with
large amplitude) For part (b), do not use the "complete
elliptic integral" function.
Instead, just use whatever software you like to evaluate
numerically, by brute force, to sufficient accuracy, the
integral, and make the plot in question.
4.39 (pendulum period,
amplitude expansion) Add part (d): Plot the analytic
result you get for the approximate
period on the same graph as the numerical result from 4.38.
4.41 (virial theorem)
4.43 (central, spherically
symmetric forces) Add part (c) Better yet, show
directly by construction that one can
find a U such that F = -
grad U.