Physics 798S

Superconductivity

Spring 2004

Homework 1

Due February 10, 2004

 

Homework Policy

            Your grade will be based on homework and a paper.  In exchange for not giving exams, I ask that you do the homework.  You may work on homework together, but not doing the homework will imperil your grade--I am willing to give bad grades if homework is not done.

            Please hand in your homework on time. I will not accept late homework, unless a valid excuse (such as illness) is given, preferably before the homework is due.

            Please do not do integrals by Mathematica when they can be done analytically.  It is fine to use Mathematica for plotting functions, or checking the results of your calculations.

 

1.  Screening in a superconducting slab.  Solve the London equations for an infinite superconducting plate of finite thickness 2t, assuming the magnetic field B0 is applied parallel to both surfaces.  Find both the magnetic field and the supercurrent inside the slab.  As examples, plot the current and magnetic field for a thickness 2t = l, and 2t = 10l.

 

2.  Drude insulator.  Following the discussion of the Drude conductor in class, consider a system of independent charges q, each subjected to a force

 


a)  Using the engineer’s time convention eiwt, find the frequency-dependent complex conductivity s(w).  Sketch this conductivity (real and imaginary parts) as a function of frequency.


b) What simple lumped-element circuit has an admittance A=1/Z with the same frequency dependence?

c)   Evaluate the integral (s = s1 – i s2)

in the case where k = 0 (Drude metal).  The residue theorem is useful.  BEWARE:  the algebra is messy; you will receive nearly complete credit for properly setting up the integral and explaining clearly how to proceed.

 


3.         Two-fluid model.  A more realistic model for a superconductor assumes that there is a density nn of normal electrons which obey a Drude-like equation

 


as well as a density ns of superelectrons which obey a London equation

a)  Using the engineer’s time convention eiwt, find the frequency-dependent complex conductivity s(w).  Assume that each “fluid” responds independently to the electric field.

b) What simple lumped-element circuit has an admittance A=1/Z with the same frequency dependence?


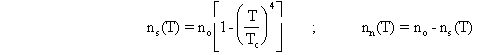
c)  Show that, in the low-frequency limit, the normal-fluid response is purely ohmic, while the superfluid response is purely inductive.  In this limit, plot s1(T) and s2(T) vs T using the empirical relationships

where no is the density of electrons in the material.  The expression for ns(T) is a fairly good approximation for the superfluid density in a clean metal, but the second expression is flawed:   ns(T) + nn(T) is not equal to the total electron density.