Solutions set 8
12-5 Use conservation of e (l = 0). The observer's initial 4-velocity is u = [(1-2M/R)-½, 0, 0, 0 ] = [hÖ5, 0, 0, 0] (from u·u = -1), therefore e = (1-2M/R)ut = 2/Ö5. At other radii, using u·u = -1,
|
|
æ
è
|
dr
dt
|
ö
ø
|
2
|
= e2 - |
æ
è
|
1 - |
2M
r
|
ö
ø
|
= |
2M
r
|
- |
1
5
|
|
|
hence
|
t = |
ó
õ
|
10M
0
|
|
æ
è
|
2M
r
|
- |
1
5
|
ö
ø
|
-1/2
|
. |
|
which works out to be (5Ö5)pM.
12-15 At ejection, energy-momentum is conserved, but not necessarily rest mass. Let p be the original 4-momentum, pL that of the eject, and pe the escaping 4-momentum, then p = pL + pe. The escaping mass receives the greatest energy if the ejected-into-black-hole matter is lightlike, so
pL2 = 0 = (p - pe)2 = p2 - 2p·pe + pe2.
But p2 = -m2, pe2 = -me2; also p ·pe = mut gtt meuet. Now note gttuet = uet = (¶/¶t)·ue = (Killing vector)·ue = -e is conserved. If the escaping spaceship arrives at infinity with zero velocity, this conserved quantity has the value -1. Also, since the original spaceship was stationary, ut = (1-2M/R)-½. Putting this all together we get a quadratic equation for f = me/m:
1 - 2 f (1-2M/R)-½ + f2 = 0
with the solution
|
f = | 1 ±(2M/R)½
(1 - 2M/R)½
|
|
|
Only the - sign makes sense, since we know f < 1. (The + sign gives 1/f.) So f vanishes when R = 2M.
12-22
a)
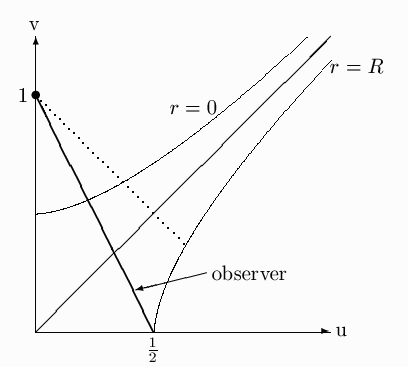
b) The straight line has a slope of 2 which means the observer is within the 45° lines that are the light cones.
c)The latest time is the value of t at which the 45° dotted line from u = 0, v = 1 intersects the curve r=R. The equation for the line is v = 1 - u. Substitute from (12.13a) with r = R, use the given expression for R, and solve for t to find t = 4M log(2).
24-6. Incompressible matter would imply an infinite speed of sound, inconsistent with SR.
Integrate (23.7) with constant r:
M(r) = 4/3 pr3 r
and insert in (23.7):
|
- |
dp
(r+ p)(r/3 + p)
|
= |
4pr3 dr
r2(1- 8pr2/3)
|
. |
|
Integrate this with the boundary condition p(R) = 0 to find
|
p(r) = r |
é
ë
|
(1-8pr2/3)½ - (1 - 8prR2/3)½
3(1-8pr2/3)½ - (1 - 8prR2/3)½
|
ù
û
|
. |
|
There is a maximum mass M(r=R) because the pressure at the center becomes infinite when M/R = 4/9 (Mmax = 4/9(3pr)-½).
24-7. a) We need l(r) and n(r). From (24.12) with m(r) = 4/3 pr3 r, as in the previous problem, we get l(r). From (34.13c) we get
|
|
1
2
|
|
dn
dr
|
= |
8prr-½
3
|
|
é
ë
|
3 |
æ
è
|
1 - |
8prR2
3
|
ö
ø
|
1/2
|
- |
æ
è
|
1 - |
8prr2
3
|
ö
ø
|
1/2
|
ù
û
|
-1
|
|
|
and this can be integrated, with the constant adjusted so as to match Schwarzschild at r = R, where
|
n(R) = log |
æ
è
|
1 - |
2M
R
|
ö
ø
|
= log |
æ
è
|
1 - |
8prR2
3
|
ö
ø
|
. |
|
The result is
|
ds2 = - |
é
ë
|
3
2
|
|
æ
è
|
1 - |
8prR2
3
|
ö
ø
|
1/2
|
- |
1
2
|
|
æ
è
|
1 - |
8prr2
3
|
ö
ø
|
1/2
|
ù
û
|
2
|
dt2 + |
æ
è
|
1 - |
8prr2
3
|
ö
ø
|
-1
|
dr2 + r2(dq2 + sin2qdf2) . |
|
b) The space part of the metric is (1 - const×r2)-1 dr2 + r2 dW2.
c) The volume inside the star is
|
V = 4p |
ó
õ
|
R
0
|
|
r2 dr
(1 - 8prr2/3)½
|
³ 4/3 pR3 |
|
