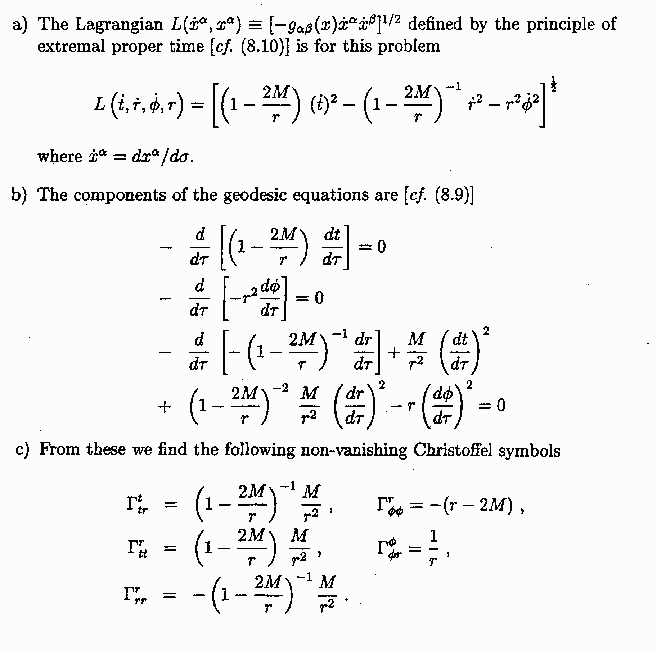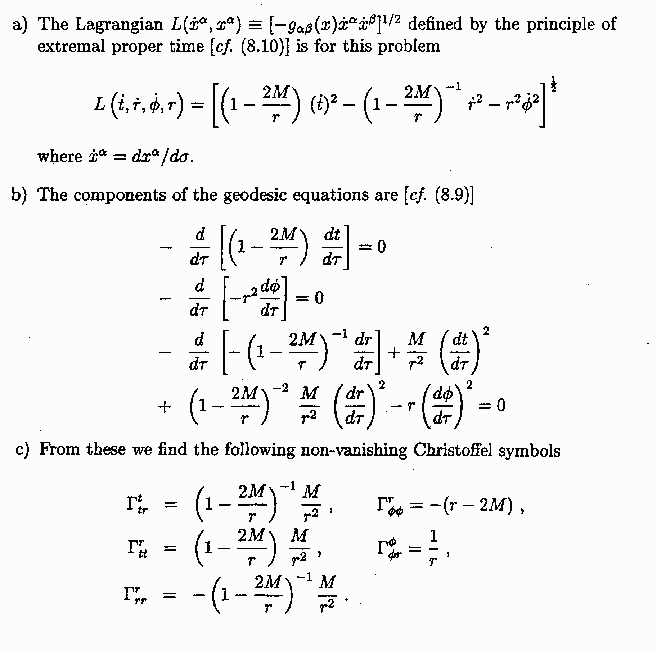7-9
a) First derivatives: the number of components of a symmetric 4×4 matrix is 10. There are therefore 10×4 = 40 first derivatives of the metric and 4×10 = 40 second derivtives ¶2xa/¶x¢b¶x¢g since these are symmetric in b and g.
b) Second derivatives: ¶2g¢ab/¶x¢g¶x"d is symmetric in both a and b and in g and d. There are therefore 10×10 = 100 conditions. The number of third derivatives ¶3xa/¶x¢b¶x¢g¶x¢d is 4×(the number of symmetric combinations of 3 indices) = 80. This leaves 20 second derivatives that cannot be made to vanish.
7-10
a) Substitute the expressions for X, Y, Z, W into X2 + y2 + Z2 + W2 and find, identically, R2. This shows that every value of c,q,f corresponds to a point on the 3-sphere. (It does not show that the coordinates cover all of the three-sphere without singularity - which is, in fact, not so.)
b) To find the metric, work out
dX = R [( sinc sinq cosf) df + . . . ]
and substitute into dS2 = dX2 + dY2 + dZ2 + dW2,
with the result
dS2 = R2 [ dc2 + sin2c (dq2 + sin2q df2 )].
8-3
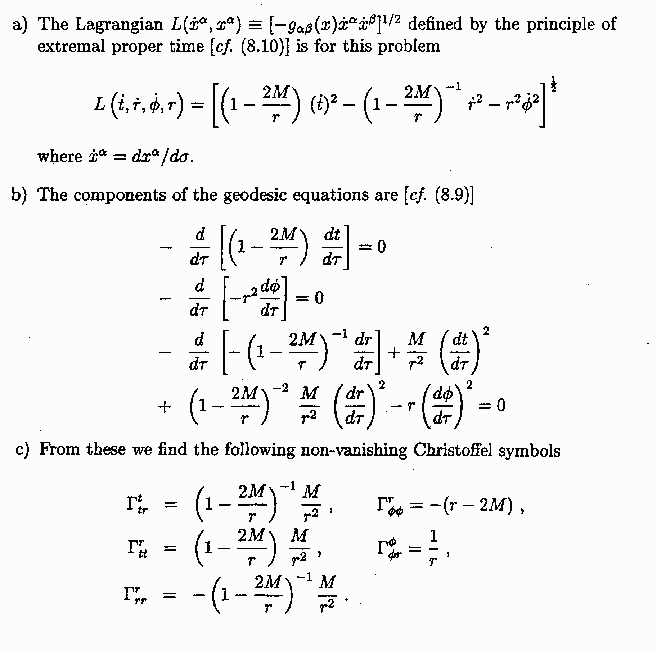
8-8 Note that the problem gives you a Killing vector (does not ask you to show that it is a Killing vector), so you can start knowing that ¶/¶f in spherical coordinates is a Killing vector. There are then many ways to find its rectangular components, for example by relating the Killing vector to angular momentum operators. One of the more straightforward approaches uses the coordinate transformation equations, x = r sinq sinf etc. and the "chain rule", ¶/¶f = (¶xi/¶f) ¶/¶xi = -y ¶/¶x + x ¶/¶y. Cyclic permutation then gives the other two Killing vectors.
8-12
a) The distance along an x-constant line to a point on the x-axis is ò0dy/y which diverges. Similarly the distance aloing any other curve to a point on the x-axis will diverge.
b) The geodesics can be obtained from the variational principle
|
d |
ó
õ
|
y-1 |
æ
Ö
|
|
dt = 0 or d |
ó
õ
|
y-2 |
æ
è
|
.
x
|
2
|
+ |
.
y
|
2
|
ö
ø
|
dS = 0 |
|
where · means d/dt resp d/dS. The first version gives the "geodesic equations" only if supplemented by the normalization, dS/dt = 1. One finds
|
|
d
dS
|
|
æ
ç
è
|
dx
y2 dS
|
ö
÷
ø
|
= 0 (1) |
|
|
|
d2y
dS2
|
= - |
1
y
|
|
æ
ç
è
|
dx
dS
|
ö
÷
ø
|
2
|
+ |
1
y
|
|
æ
ç
è
|
dy
dS
|
ö
÷
ø
|
2
|
(2) |
|
c) One has two integrals of the motion, Eq (1) above implying
dx/dS = y2/r, r = const, (1a) and the normalization,
|
|
1
y2
|
|
é
ê
ë
|
æ
ç
è
|
dx
dS
|
ö
÷
ø
|
2
|
+ |
æ
ç
è
|
dy
dS
|
ö
÷
ø
|
2
|
ù
ú
û
|
= 1 (3) |
|
We compute
|
|
dx
dy
|
= |
dx/dS
dy/dS
|
= |
y
(r2 - y2)½
|
|
|
which integrates to give (x - x0)2 + y2 = r2.
d) Use 1(a) in (3) to eliminate dx/dS, integrate:
|
y(S) = |
r
cosh(S)
|
, then from (1) x(S) = r tanh(S). |
|