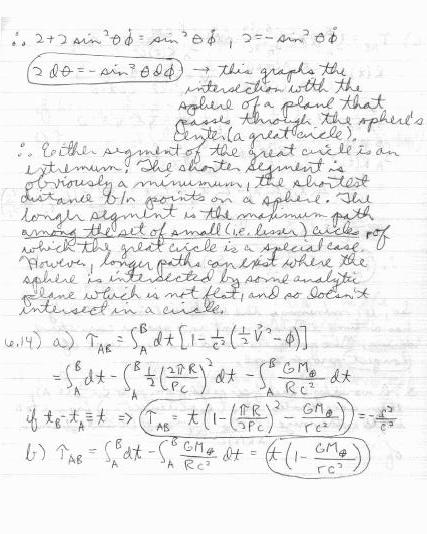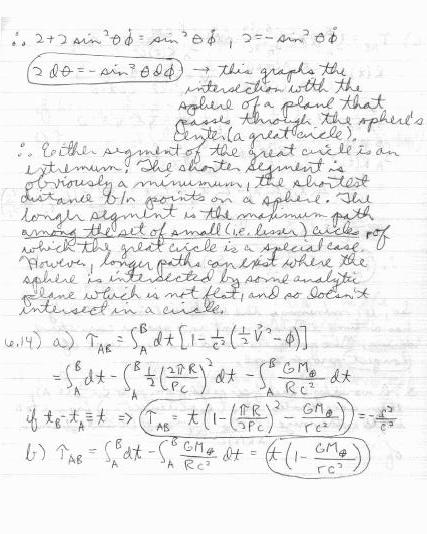
Remark on 6.12, first part: The problem does not ask you to show dI = 0 to first order (where I is the space "interval", i.e., the length of the curve) -- it tells you great circles are geodesics. You are to show that the specified curve is the shortest, not some other kind of extremum. The usual calculus procedure is to look at second derivatives. In the present case we can show it more generally. Without loss of generality we may assume a unit sphere and that the two given points are on the great circle
f = const., with 0 < q < p. The length of any (other) curve between the points, written in q, f coordinates, is given by
|
I = | ó
õ
| q2,
0
q1,
0
|
|
Ö
|
dq2 +
sin2qdf2
| = | ó
õ |
q2, 0
q1, 0
|
|
Ö
|
1 + sin2q(df/dq)2
| dq ³ | ó
õ |
q2, 0
q1, 0
| dq = q2-q1 = length of geodesic |
|
because (1 + sin2q(df/dq)2)h ³ 1 pointwise.
(This does not work for the "long" path between the points because the q,f coordinates are not good in the entire neighborhood of this path.)
The second part, as remarked, is not true. Hartle writes: "The longer segment ... provides a longer distance than any neaby path." That is not so. A path that "wiggles" around the great circle may stay arbitrarily nearby but is longer. No geodesic in Riemannian space (positive definite metric) is ever locally longest.
In spacetime, correspondingly, a short enough timelike geodesic segment is the longest distance between the two endpoint events. A world line that "wiggles" around the geodesic is shorter (twin paradox) - in fact, if it wiggles fast enough, at the speed of light, its spacetime length vanishes. Thus in spacetime no timelike geodesic is ever the shortest curve between the endpoints.
6.14 c) The proper time along any photon orbit is zero.
d) If the particle is thrown radially outward with the right velocity so that it returns in time P, that is another curve of extremal proper time.