| (21) |
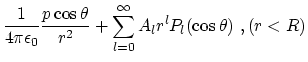 |
(22) | ||
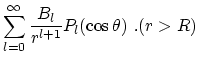 |
(23) |
The boundary conditions determine the coefficients ![]() :
:
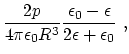 |
(24) | ||
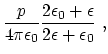 |
(25) |
and all the other coefficients are zero.
| (26) | |||
| (27) | |||
| (28) | |||
| (29) |
Here
(b) Since
![]() , the wave equation becomes
, the wave equation becomes
![]() .
.
(c) From (b), the dispersion is obtained as
![]() . If
you expand this to the first order in
. If
you expand this to the first order in ![]() , you obtain
, you obtain
| (30) |
Since ![]() is the factor that exhibits the anomalous
dispersion, the correction term to the absorption coefficient will
still show the anomalous dispersion in such a conductor.
is the factor that exhibits the anomalous
dispersion, the correction term to the absorption coefficient will
still show the anomalous dispersion in such a conductor.
| (31) |
(b) The electric field at the solenoid surface satisfies
![]() , and the magnetic fiels at the axis of the ring is
, and the magnetic fiels at the axis of the ring is
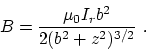
Therefore, the Poynting vector is
| (32) |
| (33) |
(b)
![]() where
where
![]() . Time-averaged,
. Time-averaged,
![]() .
.
(c) The radiation damping force is
![]() . If you take the time integral of
. If you take the time integral of ![]() , then you
obtain
, then you
obtain ![]() . In other words, the energy loss of the particle due
to the damping is the radiated power.
. In other words, the energy loss of the particle due
to the damping is the radiated power.
Next: About this document ... Up: Final Examination Previous: Questions Hyok-Jon Kwon
2001-12-19