(a) Suppose that
![]() . Then very close to the centre
of the sphere, what is the approximate form of the electric potential
as a function of the distance
. Then very close to the centre
of the sphere, what is the approximate form of the electric potential
as a function of the distance ![]() from the centre? (10 points)
from the centre? (10 points)
(b) With a finite ![]() , write down (i) the equation for the electric potential inside and
outside of the void, and (ii)
the boundary conditions on the potential at the surface of the void.
(10 points)
, write down (i) the equation for the electric potential inside and
outside of the void, and (ii)
the boundary conditions on the potential at the surface of the void.
(10 points)
(c) Solve the equation and the boundary conditions to find the electric potential both inside and outside the void. (20 points)
(a) Assuming a medium with no free charge or free current with a
frequency-dependent dielectric constant
![]() , rewrite
the four Maxwell's equations in the frequency and wave-vector
domain. Hint: Fourier transform the Maxwell equations.
(10 points)
, rewrite
the four Maxwell's equations in the frequency and wave-vector
domain. Hint: Fourier transform the Maxwell equations.
(10 points)
(b) Now we consider a conductor where the charge-currents are induced
by the electric field (
![]() where
where ![]() is
the constant conductivity). Modify the Maxwell's equations obtained in
(a) and derive the electromagnetic wave equations in the
is
the constant conductivity). Modify the Maxwell's equations obtained in
(a) and derive the electromagnetic wave equations in the
![]() domain. (10 points)
domain. (10 points)
(c) Conductors also contain bound electrons which give a dielectric
constant
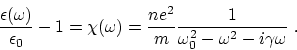 |
(19) |
| (20) |
(a) What are the electric and magnetic fields at position
![]() for
for ![]() ? (10 points)
? (10 points)
(b) What is the total power radiated from this charge? (10 points)
(c) What is the radiation damping force felt by the charge? (10 points)
(d) Explain the relation between the damping force in (c) and the answer to (b). (10 points)
Next: Solutions Up: Final Examination Previous: Final Examination Hyok-Jon Kwon
2001-12-19