Assignment 9 Solutions
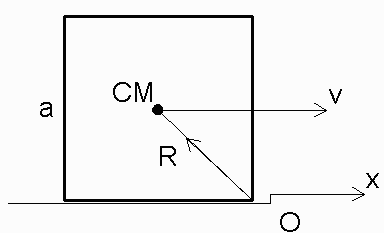1. (Problem 10.16 **)
(a) The moment of inertia of the cube about any edge is
worked out in Example 10.2 and is given by (10.47) as 2/3Ma2. During the collision, kinetic energy will be lost (the
collision is inevitably inelastic), but the angular momentum Lyabout the edge of the step is conserved. (I take the x direction
as that of the incident velocity, as shown, and y into the page.) Just before the collision the angular momentum is åma ra ×v = MR ×v, so that Ly = Mav/2. Just after the collision, the cube is rotating about the edge of the step and
Ly = Iyy wo
= 2/3Ma2 wo. Equating these two
expressions for Ly, we find that wo = 3 v/(4 a).
(b) If the initial speed is small, the cube's rotational motion about O will stop before the CM has passed the step, and
the cube will fall backward. If v is big enough, the CM will pass the step and the cube will roll forward. At the critical
speed that divides these possibilities, the CM will just come to rest vertically above O. Since mechanical energy is conserved
in the rotational phase of motion, this critical speed is determined by the condition
|
1/2Iyy wo2 + M g a/2 = M g a/ Ö2. |
|
(The height of the CM above O is a/2 initially, and a/Ö2 when the CM is vertically above O.) Substituting
for wo from part (a), we can solve for v and find vcrit = [8 (Ö2 - 1) g a/3]1/2.
2. (Problem 10.32 **)
(a) Let us choose the principal axes as our coordinate directions. Then
|
l1 = |
ó
õ |
r(y2 + z2)dV and l2 = | ó
õ |
r(x2 + z2)dV. |
|
Adding these two equations, we get
|
l1 + l2 = |
ó
õ |
r(x2 + y2) dV + 2 |
ó
õ |
rz2 dV ³ |
ó
õ |
r(x2 + y2) dV = l3. |
|
(b) The " ³ " in the above relations is an "=" if and only
if all parts of the body have z=0, that is, the body is a lamina lying in the plane z = 0.
3. The point of course is to find the moments of inertia. Let the length of the cylinder be h and the mass, M. The moment about the
symmetry axis is the same as that for a disk, l3 = 1/2Ma2.
For the transverse directions we can use the equation of problem 2,
|
l1 = 1/2(l1 + l2) = 1/2 l3 + | ó
õ |
rz2 dV = 1/4 Ma2 + 1/12 Mh2 |
|
Putting this equal to l1 tells us h = a Ö3.
4. (a) Because D and the disk's point of contact P are momentarily
fixed, the angular velocity w must be horizontal,
parallel to the line PD. The point C is at a distance
ab/(a2+b2)1/2 from the plane, and a distance
b2/(a2+b2)1/2 from the vertical (dotted) axis. Its speed
v_CM must be the same whether computed from w or
wz:
|
vCM = w |
ab
(a2+b2)1/2
|
= wz |
b2
(a2+b2)1/2
|
|
|
hence w = (b/a)wz. (A simpler way
to see this is to decompose w into a vertical part
(of size wz) and a part along CD). The components of
w in principal axis (the 3-axis being the disk's axis
of symmetry CD) are
|
w3 = - w |
b
(a2+b2)1/2
|
= - wz |
b2
a(a2+b2)1/2
|
w1 = w |
a
(a2+b2)1/2
|
= wz |
b
(a2+b2)1/2
|
|
|
Therefore the angular momentum is
|
L3 = 1/2 Ma2w3 = - 1/2M wz |
ab2
(a2+b2)1/2
|
L1 = 1/4Ma2 w1 = 1/4M wz |
a2b
(a2+b2)1/2
|
. |
|
The kinetic energy is
|
T = 1/2 w(I)w = 1/2 MvCM2 +1/4Ma2w32 + 1/8Ma2w12 = |
Mwz2b2
8
|
|
æ
è
|
6b2 + a2
a2 + b2
|
ö
ø
|
|
|
(b) Consider taking torques about the momentarily fixed bottom
point of the disk, so that the unknown reaction forces do not
enter. L precesses with angular velocity wz about
the vertical axis (not with angular velocity w about its
axis). So in L· = wz z only the horizontal component
of L counts. Since w is horizontal, that is also the
component in T = 1/2w·L, so we have*
|
|
×
L
|
= wz (2T/w) = |
Mwz2 ab
4
|
|
æ
è
|
6b2 + a2
a2 + b2
|
ö
ø
|
= Mg |
a2
(a2+b2)1/2
|
|
|
where the last term is the torque due to
gravity. Since no torque from the shaft was added, this will give
the critical
|
wz2 = |
4a
b
|
|
æ
è
|
(a2+b2)1/2
6b2 +a2
|
ö
ø
|
g . |
|
*note wz/w = b/a. The notation is a bit confusing,
since w is the total angular velocity, but wz is
not its component in a rectangular system. (It should never have
been called wz)
5. If we write out v = ω×r in components then the first condition
tells us ωy = –5, ωz = 2. Subsitute in the same equations to find for the second particle vx = –5 (as wll as
vz = 0, but vy is undetermined because ωx is unknown).