Next exam: Friday April 21, 1 hour, on chapters 8-10.
To complete your reading of chapter 10, look at problem 10.21, 10.33 that contain results derived in lecture but not in the main text.
You may also want to look at this applet* showing the torque-free motion of a rigid body (rotating not about a principal axis)
And here is a movie of the general case (3 different principal moments). Finally, here is something more -- much more -- about angular dynamics (including a Feynman story on p. 69).
*one of you may prefer this version
- Text, problem 10.16. Just use the result of problem 10.15
- Text, problem 10.32. Hint: problem 10.23
- Find the length of a homogeneous solid circular cylinder of radius a, given that all its principal moments of inertia are equal
-
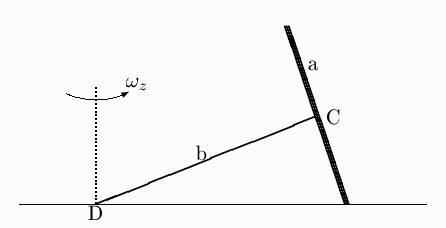 A uniform circular disk of radius a and mass m is rigidly mounted on one end of a thin massless shaft CD of length b.
The shaft is normal to the disk at its center C. The disk rolls without slipping on a horizontal plane with the end D resting at a fixed point on this plane.
The center of the disk rotates about the vertical through D with constant angular velocity ωz.
A uniform circular disk of radius a and mass m is rigidly mounted on one end of a thin massless shaft CD of length b.
The shaft is normal to the disk at its center C. The disk rolls without slipping on a horizontal plane with the end D resting at a fixed point on this plane.
The center of the disk rotates about the vertical through D with constant angular velocity ωz.
- Find the disk's angular velocity, angular momentum of about C, and kinetic energy.
- If ωz exceeds a certain maximum value, the end D of the shaft will lift off the table.* Find the maximum ωz
*Roughly: the centrifugal force on the disk gets too large for gravity to keep the disk tilted.
But you are advised against doing the problem that way, because the Coriolis force also contributes. Insted do it in an inertial frame, using the idea that at the critical ωz the shaft exerts no torque.
- A rigid body is turning about a fixed point O, and OXYZ are rectangular axes. If at some moment the velocity components of the particle with coordinates (1, 0 , 0) are (0, 2, 5), find vx, the component of velocity in the direction of the X-axis,
of the particle with coordinates (0, 0, 1)