Fifth Assignment, due Feb 24 -- solutions
First hour exam is coming up March 3, 10-11 am. It will feature Lagrangian problems like those on assignments 4 and 5.
All the interesting problems in chapter 7 are odd-numbered (answers in back), so I had no alternative but to modify them. The given answers will still be useful as special cases to check your answers.
Problem 1 is the famous Atwood-monkey problem that can be (and has been) discussed for hours in order to find a "trivial" solution without writing any equations. You can do it in a shorter time by Lagrangians.
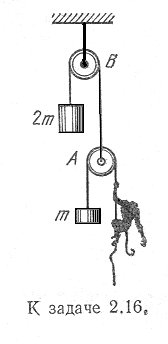
- A monkey of mass m is balanced by a counterweight across the pulley A. The pulley A is balanced by a weight across pulley B. Initially the system is at rest. How will the weight 2m move if the monkey begins uniformly to haul in the rope with speed u relative to himself? Neglect the masses of the pulleys and ropes.*
Also assume the pulleys turn without friction. The assumption of uniform speed is not necessary. If the monkey hauls in a length of rope ΔL, how far (and in what direction) does 2m move?
- Text, problem 7.29 BUT P is not forced to rotate, instead the circle is the boundary of a massive uniform disk (moment of inertia ½MR²). Find Lagrange's equations for this system of two degrees of freedom.
- Text, problem 7.37 BUT let the two masses be general, m (on the table) and M (hanging down). This is closely related to problem 7.38.
- Text, problem 7.41 BUT let the wire shape be z = kρ³. What is the conserved Hamiltonian?
- Text, problem 7.46
*Обезьяна
массы m
уравновешена
противовесом
на блоке A.
Блок A
уравновешен
грузом на блоке
B. Система
неподвижна.
Как будет
двигаться
груз 2m, если
обезьяна
начнет
равномерно выбирать
веревку со
скоростью u
относительно
себя? Массами
блоков и
трением пренебречь.

