Physics 410First Hour Exam March 10, 2005



Instructions: Answer both questions in an exam booklet. Don't forget to sign the pledge.


Problem 1
a. A force F acts on particle of mass m in 3D space. The force is derivable from a potential, F = - grad U. Show that Newton's second law follows from Lagrange's equations for the particle.
The Lagrangian is L = 1/2m(x·2 + y·2 + z·2) - U. Lagrange's equations become
px = L
x·
 = m
×
x
 
   etc.     L
x
 = - U
x
 = Fx     so   
×
px
 
 = m
××
x
 
 = Fx
and similarly for y and z.
b. A hill is in the shape of half a cylinder of radius R. The speed of a bug crawling on this hill is proportional to its height above the base. The bug wants to know along what path it should crawl in order to get between two fixed points on the hill in the least time. Choose suitable coordinates and set up an integral whose variation will determine the path. (Do not work out the variational equations, but make sure that your integral is a line integral containing no undetermined functions other than those specifying the path)

The speed of the bug is v = ds/dt hence the time it takes to go a distance ds is dt = ds/v. Here ds is the distance along the cylindrical hill. We choose coordinates z and , then ds2 = dr2 = dz2 + R2 dq2. Unfortunately that's not in the form (vector)·dr, so to write a line integral over ds we have to choose a parameter along the curve. That could be a new parameter, say t, or one of the two, z, q. The time to be minimized is then, in all three varieties (with ' = d/dtau)
t = ó
õ		ds
v
 µ ó
õ 		ds
R sinq
 = ó
õ 		(z¢2 + R2q¢2)½
R sinq
dt = ó
õ		[(dz/dq)2 + 1]½
R sinq
 dq = ó
õ 		[1 + R2(dq/dz)2]½
R sinq
dz
Any of the last three forms would be acceptable; the curve is described by (z(t), q(t)) or z(q) or q(z), respectively. The last form may be the simplest if you had to solve for the curve because the integrand L does not depend on z, hence
L
(dq/dz)
 = 2R2 (dq/dz)
[1 + R2(dq/dz)2]3/2 R sinq
 = const
is a first integral.


Problem 2

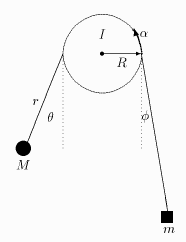
The figure on the right shows an Atwood's machine made somewhat more realistic because the point masses m,   M at the ends of the string of length l+pR are allowed to "swing", but they remain in the plane of the paper. For simplicity, assume that the string is always in contact with the upper half of the wheel, bends at the height of the axle, and is straight below that, as drawn. The wheel has radius R and moment of inertia I, and everything is frictionless (except static friction between wheel and string that keeps the string from slipping along the wheel). We assume the two masses do not collide and the strings attached to them do not get entangled. Gravity g is acting. We consider two cases:
(1) the wheel is rotating freely in response to whatever torque the strings exert
(2) the wheel is driven to rotate clockwise with constant angular speed w.


a. How many degrees of freedom does the system have, and which generalized coordinates do you choose to describe it in the two cases? Clearly specify your coordinates by a drawing, either of your own or on this page which you will then hand in with you exam book.

Case (1)
The system has 3 degrees of freedom, the coordinates can be q, f and r, or q, f, and a (or other functions of these)
Case (2)
Here a = wt is specified (hence r = Rwt + const), so only two degrees of freedom remain.
b. Mention at least two and no more than three special cases (special values of the given parameters, of your coordinates, ...) for which your general knowledge of physics tells you what the equations of motion will be, without having to compute anything, and give those equations. Be careful to specify your special cases completely, telling whether the wheel is free or constrained, and give as many equations of motion as generalized coordinates.
If your general knowledge includes the simple Atwood machine (Case (1), q = f = 0 = I) that could be one case (The same for case (2) has no degrees of freedom left). But the simplest special case is maybe g = 0, q = 0 = f Then in case 1 dr/dt = const. Another simple case is case (1) m = 0 = I, then M will be in free fall. Or case (2) w = 0, then we have two independent (uncoupled) pendula.
c. Now pick one of the cases (1) or (2) and write the Lagrangian for the system.
For case (1) and with r as the third coordinate, the two masses are specified by their polar coordinates (the radial distance of m is l- r), so we can use the polar coordinate expression for v2. The potential energy of each mass is proportional to its distance (e.g. r cosq) below the axle, hence
L = T - V = 1/2M(
×
r
 
 2
 
 + r2
×
q
 
 2
 
 ) + 1/2m(
×
r
 
 2
 
 + (l-r)2
×
f
 
 2
 
 ) + 1/2I(
×
r
 
 /R)2 + Mgrcosq+ mg(l-r)cosf
For case (2) we replace r·/R) by w.
d. Write the equations of motion that follow from the Lagrangian in c. Check that they agree with one of the special cases you mentioned in b.
For case (1) we get three equations:
(M+m+I/R2)
××
r
 
 - Mr
×
q
 
 2
 
 + m(l-r)
×
f
 
 2
 
 - Mg sinq + mg cosf = 0

Mr2
××
q
 
 + 2Mr
×
r
 
×
q
 
 + Mgrsinq = 0

M(l-r)2
××
f
 
 - 2M(l-r)
×
r
 
×
f
 
 + Mg(l-r)sinf = 0
 (These equations are coupled and can't be solved in closed form. In case (2), replace r by wt and forget about the first equation.)
e. Is there a conserved quantity for your case? If so, tell what it is (by name or better by formula).
In case (1) the Hamiltonian is conserved,
H = T + V = 1/2M(
×
r
 
 2
 
 + r2
×
q
 
 2
 
 ) + 1/2m(
×
r
 
 2
 
 + (l-r)2
×
f
 
 2
 
 ) + 1/2I(
×
r
 
 /R)2 - Mgrcosq- mg(l-r)cosf
In case (2) the Lagrangian has irremovable time-dependence, and no other symmetry, so there is no conserved quantity.

File translated from TEX by TTH, version 3.60.
On 14 Mar 2005, 18:11.