Solution to First Assignment: due Friday, January 28, 10 am.

  1. Text, problem 2.4 a, b: (Wording of problem given only on this first assignment, for those who do not yet have the text)
    The origin of the quadratic drag force on any projectile in a fluid is the inertia of the fluid that the projectile sweeps up.
    (a) Assuming the projectile has area A (normal to its velocity) and speed v, and that the density of the fluid is r, show that the rate at shich the projectile encounters fluid (mass/time) is rAv.
    (b) Making the simplifying assumption that all of this fluid is accelerated to the speed v of the projectile, show that the net drage force on the projectile is rAv².
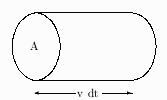(a) In a time dt the area A sweeps out a volume A×(v dt), of mass   dm = rAv dt,   hence   dm/dt = rAv.

(b) This mass starts at rest and gains speed v, hence acquires a momentum  

dp = dm · v = (rAv dt)· v  
in time dt. (It is best not to commit oneself whether this is due to the change in mass or the change in velocity -- the momentum is what really counts in Newton's law)

Therefore the force is F = dp/dt = rAv².
  1. Text, problem 2.21:
    A gun can fire shells in any direction with the same speed v0. Ignoring air resistance and using cylindrical polar coordinates with the gun at the origin and z measured vertically up, show that the gun can hit any object inside the surface
    z =   v0²
    2g    		  -    g
    2v0²    		  r²
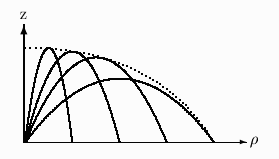To visualize what is goig on it helps to draw a diagram of several trajectories. (The dotted curve is the desired limit) Then there are several ways of doing this, for example one can verify that no point on a trajectory is outside the given surface: for a trajectory we know r = (v0 cos q) t and Z = (v0 sin q) t - ½ gt² (where Z refers to a trajectory, to distinguish it from the z of the limiting surface). Eliminating t gives
Z = (tan q) r -       g r²
2v0² cos²q		                   (*)
Calculate
Z - z = a - u + u²/a

where a = v0²/2g and u = r tan q. Now the problem amounts to showing Z - z > 0. This is done by minimizing with respect to u, and showing that Z - z = 0 at the minimum.

Another way to find the limiting curve is to note that for any fixed r, the limiting surface occurs at the highest z that is reached for any angle q. Therefore, differentiate (*) with respect to q, treating r as constant, and set result to 0:
0 =       r
cos²q		   -   g r²
2 v²		    2 sinq
cos³q
Thus   r = (v²/g) cot q -- this is where the trajectory starting at q touches the limiting surface. Of course Eq (*) is also valid there. Eliminating q between these equations gives the cited equation for the surface.