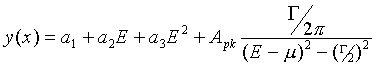
Homework assignment # 5

These are exercises 9.1 and 9.3 from Bevington. The purpose is to develop some experience with using either Mathematica or the DOS program ANALYSIS to fit a peak that lies on top of some background.

Figure 9.1 in Bevington shows some data from a counting experiment of 2000 events as a function of energy. The data are in bins of 0.05 GeV, between 0 and 3 GeV.  The data are
in this file.

a) Using either the Mathematic notebook provided (you'll have to modify it), or the DOS program analysis, read in the data and fit it to a quadratic background and a single Lorentzian peak. The fitted function should be

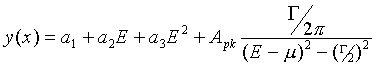
b) From the data, find the area of the peak by summing up all counts in the region surrounding the peak and subtracting the estimated background. Estimate a correction for how many events are in the tails of the peak. Estimate the uncertainty in your determination of the area. Assume the data have statistical errors only.

c) Find the number of counts in the peak from your fit and compare to your estimate. Be sure to quote an error on your determination of the number of counts, and show how you arrived at the error. Compare the parameters of your fit to the following parameters obtained by Bevington.  Determine chi-squared for the fit.

a1 = -0.87 +- 0.89
a2 = 46.1 +- 2.6
a3 = -13.4 +- 2.2
Apk = 13.8 +- 2.2
m = 0.987 +- 0.011
G = 0.172 +- 0.035

d) Repeat the fit with adjacent bins summed merged and observe the effect on the value of chi-squared and the determination of the area of the peak.