Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

In our last class on using Fourier Series, we showed that for the harmonic oscillator equation

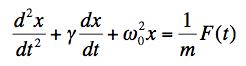
with a driving function, F(t), that the particular solution of the damped harmonic oscillator took the form

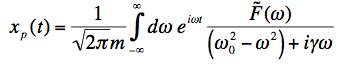
where

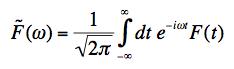
is the Fourier transform of the driving term.

Use contour integration techniques to evaluate this integral assuming that the F.T. of F is an analytic function of ω in the upper half of the complex ω plane and that it vanishes on the circle at infinity.

Solution

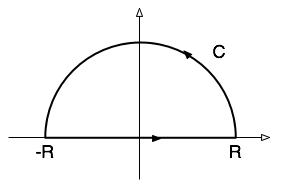
Since F(ω) vanishes on the circle at infinity, we may write the integral for the particular solution as a contour integral: where C is the contour as shown in the figure at the right (after R is taken to infinity).

To solve this, we can use the residue theorem. For that, we have to find the poles. By the fundamental theorem of algebra, we can factor the denominator by finding the places where it vanishes.

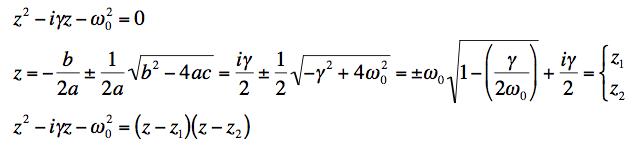
This allows us to write our integral as:

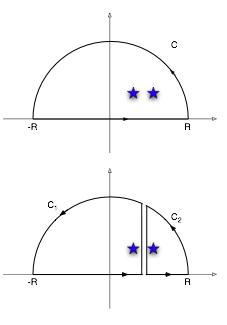
The countour can now be divided into two as in the picture at the right so: Since we have expressions for z1 and z2 and for the FT of F, we can plug in and get our result.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 13. December, 2005.