Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

(a) Explain what is meant by a function of two variables x and y being analytic and discuss why we might want to work with such functions.

(b) Consider the following three functions of the two variables x and y and determine which of them are analytic when considered as functions of z = x + iy.

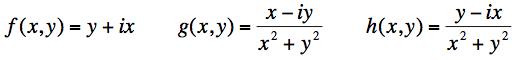
Demonstrate your conclusions in two ways: by using the Cauchy-Riemann equations and by rewriting them as a function of z and z*.

(c) Are these three functions all analytic everywhere in the x-y plane? If not, specify where they are and where they are not.

Solution

(a) A function of two variables is analytic at a point z=a in the complex plane if the derivative defined at a point by the normal derivative rule (but now using the "extended number", z = x+iy, as the variable):

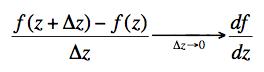
This is trickier than for 1 variable, since we can choose Δz in a variety of ways -- taking either Δz = Δx or Δz = Δy or some combination of the two. We could in principle get different results depending on how we did it. There are lots of examples of this. If you consider Sqrt(z) and take the derivative at 0 along the real axis approaching from the positive direction you get a real number (-- actually an infinite real number). If you take the derivative approaching from the negative direction you get an imaginary number (-- again an infinite one).

The reason this is valuable goes well beyond the satisfaction of not having to specify which direction you are coming from when you are taking a derivative. Functions that have this property are dramatically constrained. For example, if a function is analytic at every point in a region and we know it on every point on a closed curve in that region then we can find it at every point inside the closed curve using the residue theorem. Many integrals that are otherwise extremely difficult to evaluate can be easily done analytically.

The particular reason we are interested is that there are physical implications. A function that satisfies the C-R equations also satisfies the Laplace equation and many physical properties (electric potential, for example) satisfy the Laplace equation. The integrals that frequently appear from solving ordinary differential equations by the Fourier (or Laplace) transform method are often do-able using complex contour integration methods that follow from analyticity.

(b) First consider f. Does its real and imaginary parts satisfy the C-R equations?

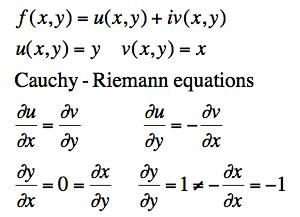
Nope. Now let's express f as a function of z and z*.

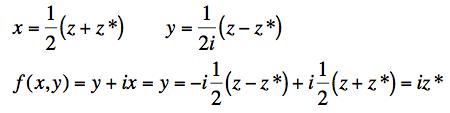
So f is not analytic.

Now consider g:

It satisfies the C-R equations. Can we see why by expressing it in terms of z and z*?

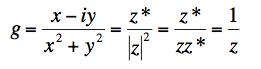
Since it's only a function of z it is analytic.

What about h?

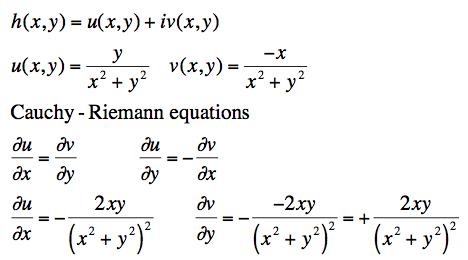
So it doesn't satisfy the first C-R equation. Can we see why by writing it in terms of z and z*?

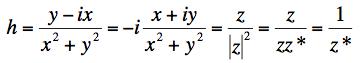
It's only a function of z* so it is not analytic.

(c) The only function that is analytic is g. It does have a pole at 0 so it is not analytic there -- only everywhere else.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 13. December, 2005.