
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for Edward F. Redish |
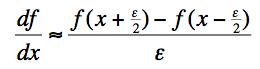
The derivative is defined as the limit of the right hand side above as ε approaches 0. Demonstrate that this is correct to O(ε2) using the Taylor series and show what it means graphically in terms of the slope of the tangent to the curve.
(b) The integral of the function f is defined as the limit of the Riemann sum:
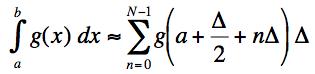
where Δ = (b-a)/N. The integral is defined as the limit of the right hand side above as N approaches infinity. Give a graphical interpretation of this result explaining why the argument of the g on the right is what it is.
(c) Combine these two results by considering the integral of the function
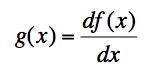
and using the approximation for the derivative with ε = Δ. Demonstrate the result (the fundamental theorem of calculus)
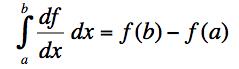 .
.
Solution
(a) The correctness of the result to order ε2 can be demonstrated using the Taylor series for the shifted functions:
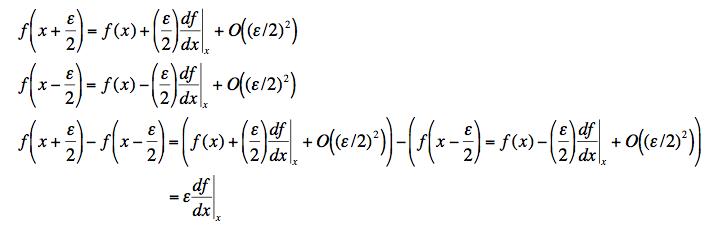
|
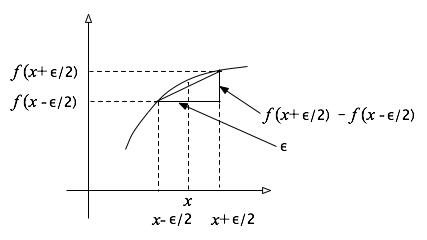
The graphical
description is shown at the right. The values ε/2 and -ε/2
are symmetrically displaced around the point where we want to find
the derivative. The ratio we have shown for the derivative is the
rise/run (the tangent of the slope) of the chord to the curve as
shown.
|
 |
|
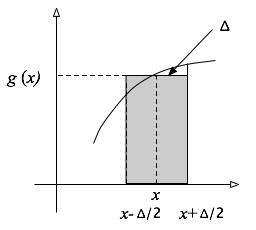
(b) If we divide the x range into N equal bins, the bins will have the size Δ = (b - a)/N. We want the area of the curve by adding up the area in each of the Delta bins. A decent approximation is to take the area of the bin as the width of the bin (Δ) times the average height of the bin, taken as the value of g evaluated at the mid-point of the bin. This is shown in the figure at the right with the center of the bin being represented as x. For our bins, the center of the bin will be at x = a+nΔ + Δ/2. This gives the desired result. |
 |
(c) If we take g = df/dx and use the form in (a), taking ε = Δ, and put it into (b) the result is:
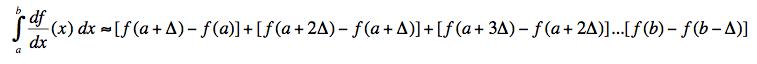
All the terms cancel except the end terms (the vertical bar cancellations in the expression below indicates a cancellation with the next or previous (unshown) term) giving the fundamental theorem of calculus.
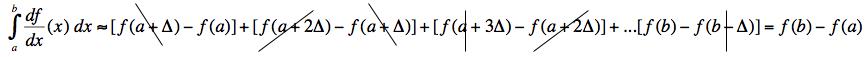
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 11. December, 2005.