Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

In a 2-D Cartesian vector space the basis is expressed in Dirac notation as An arbitrary vector is expressed in this basis as Suppose we consider a new basis rotated from the first by an angle θ as shown in the figure at the right:.

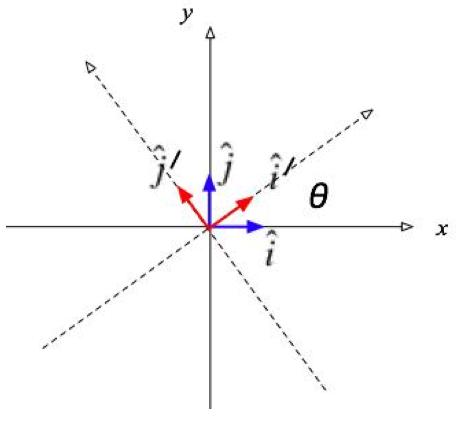(a) Construct the 8 dot products

.

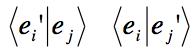(b) Use the dot products you have constructed to express the coordinates of the vector |A> in the new basis, a₁', a₂', in terms of the old coordinates, a₁, a₂.

Solution

(a) The dot products are easily read off the graph. They are either a sine or a cosine and either positive or negative. The result for the first four is:

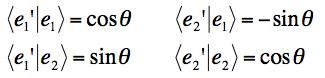
The result for the transposes of these is the same since <e'_i|e_j> = <e_j|e'_i>*. Since they are all real the transposes of the dot products are the same.

(b) Writing |A> in two ways and taking the dot product of both equations with the primed basis states we get the results

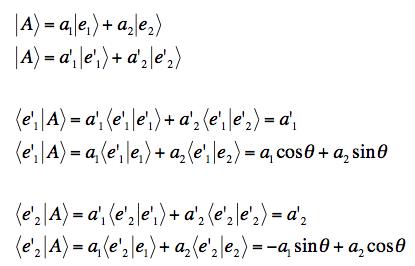
Therefore we can conclude

RETURNS

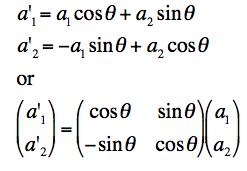
University of Maryland	Physics Department	Physics 374 Home

Last revision 15. November, 2005.