Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

In lecture we demonstrated that the shape of a string plucked in the center:

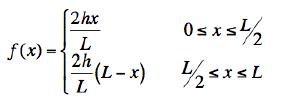
could be expanded in a Fourier series

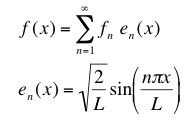
with Fourier coefficients:

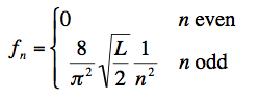
(a) If at time t = 0 the string is plucked in the center so that when it is released:

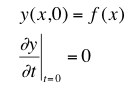
then find an expression that will give the shape of the string for all times, y(x, t).

(b) Assuming that it is OK to ignore any damping or internal friction, will the string ever resume its original shape after it has been released? If so, will it do it regularly? If so, with what period? Explain carefully how you came to your conclusion.

(c) Suppose that instead of plucking the string in the center, you plucked it 1/4 of the way from one end to the other. Answer the same question as in (b).

Solution

(a) We know that the time dependence of each normal mode, e_n(x), is that it oscillates with the frequency ω_n. By this, we mean that the time dependent solution for the normal mode is:

(where we use the cos with a phase rather than separate sin and cos terms for ease of handling -- though both ways work). This means our general solution as a function of time will be:

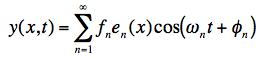
We determine the phase Φ_n by fitting the initial conditions:

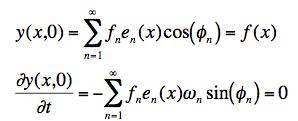
To match the initial conditions, we have to take all the Φ_n = 0 . This gives the result for the time dependence

.

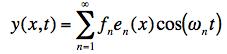(b) The string will return to its original shape if all of the cos terms ever get back to 1. The first term becomes 1 when ω₁t becomes 2π times any integer. At any time that ω₁t = a positive integer times 2π then ω_nt = nω₁t also equals a positive integer times 2π. So the shape will repeat with the period of the first mode, 2π/ω₁.

(c) Trick question. As long as the series contains a first term, when it repeats doesn't depend on the coefficients. It will repeat with the same period. If the string is started in a shape that prevents the odd terms from contributing (i.e., all the f_n = 0 for odd n), then the period would be the period of the first even term -- half the period found in (b).

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 29. November, 2005.