Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

Two identical wheeled carts of mass m are connected to a wall and each other as shown in the figure below. The two springs have spring constants k and a rest length l0.

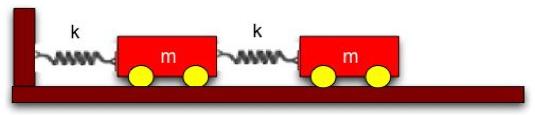(a) Choose a convenient coordinate system for describing the positions of the carts and write the equations of motion for the carts. Be sure to specify your coordinate system.

(b) Do you have some way to check that these equations are right? Describe one check you made.

(c) Find the frequencies of oscillation of the possible normal modes of the system.

(d) Our "standard normal modes" 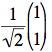and 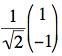that we have found for many systems are not normal modes of this system. Explain why not. (You don't have to find the actual modes.)

Solution

(a) Let's choose the coordinates for each mass as starting from the situation where both springs are at their rest length and there is no force on anybody. (We are assuming that these spring satisfy Hooke's law even when they are compressed.) Then take the displacement of cart 1 to the right from that position as positive and the same for cart 2. These are shown in the figure below. The picture is shown with the carts at equilibrium (no net force). As the carts displace, the coordinate for each cart is read off its own coordinate axis.

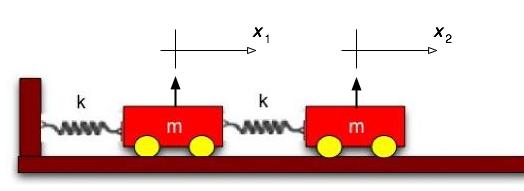
As the carts displace, the springs are stretched or squeezed and exert forces according to the amount of stretch or squeeze. The equations are respectively:

.

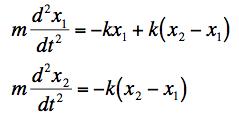(b) We can check the signs in this by holding cart 2 at its origin and displacing cart 1 in the positive dirction. The left spring pulls it back to the left and the right spring pushes it back to the left. If cart 1 is held at its origin and cart 2 is pulled to the right (positive), then the middle spring pulls cart 1 on the right and cart 2 to the left. These agree with what we have written.

(c) Rewriting the equations by defining the natural frequency, ω² = k/m, the equations become

Putting in the normal mode ansatz, x_n = A_n e^iωt we get

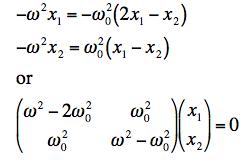
We know we can only get a non-trivial solution to this if the determinant of the matrix vanishes. This picks out particular allowed values of omega. To solve this more easily, we factor out an ω₀² and define λ = ω²/ω₀². The determinant equation then becomes:

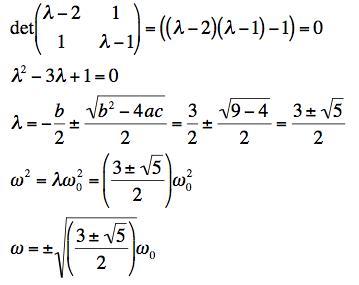
(d) Our "standard" normal modes occur when both masses feel identical restoring forces for identical displacements. This doesn't happen here because the situation is not symmetric for the two masses. Mass 1 is attached to 2 springs while mass 1 is only attached to a single spring.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 29. November, 2005.