Problems for
Intermediate Methods in Theoretical Physics

Edward F. Redish

An Orthonormal
Basis for a Function Space

Consider the space of functions of the form

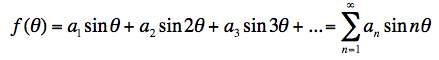
Let's create an orthonormal basis for this space.

(a) First, demonstrate that the functions sin nθ form an orthonormal set; that is, prove that

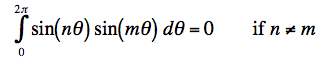
(b) Next, find constants An such that if we define basis functions en = An sin(nθ) then

.

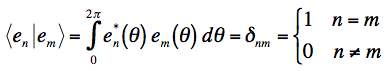Solution

(a) This is most easily done by making the complex expansion of the sin terms and observing that the integral of exp(inθ) vanishes if n is not zero.

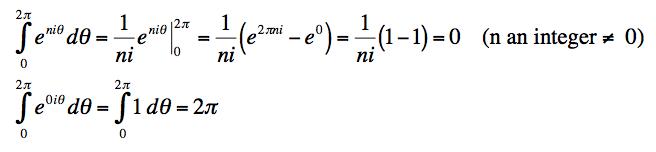
So we get

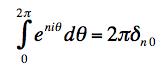
Now if we do the integreal of the product of the sines we get

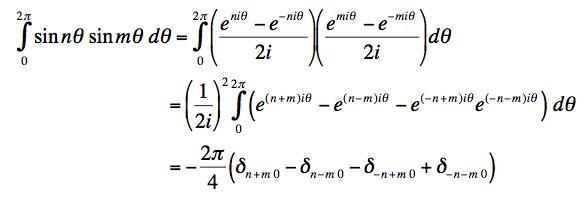
If we assume that n and m are positive then only two of the terms can be non-zero and we get

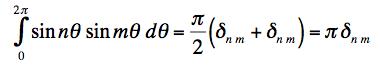
This means that the functions are orthogonal.

(b) To make them orthonormal, we define the basis vectors:

RETURNS

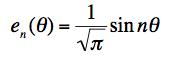
University of MarylandPhysics DepartmentPhysics 374 Home

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 15. November, 2005.