Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

When I came into the seminar room across the hall for my office for a meeting last night, I found the set of equations at the right on the white board. After a short consideration, I decided I knew what problem they were solving. Write a physics problem for which the equations at the right could form a reasonable solution. Be sure that you write the full problem, identifying all the symbols that appear in the answer (the last line). They should be natural labels, not contorted. (For example: It would NOT be natural to say: "An object falls a distance 2L." Why should that distance be labeled "2L" rather than "L"?)

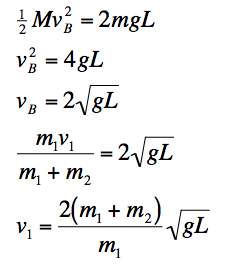Solution

First, it would be a good idea to check the dimensions of all the equations to make sure they are reasonable. As is typical in physics (not so often in math), the specific symbols chosen indicate the kind of quantity we are talking about. So let's assum that M, m and m are masses, v and v are velocities, g is the gravitational field, and L is a length. By cancelling the units of the various masses, we can see all the units work if [v²] = [gL]. Since (L/T)² = (L/T²)L they all work.

The first equation suggests some kind of energy conservation. An object with a mass M falls a distance 2L. Why are there two different m's and why is the distance the object has fallen equal to 2L instead of just L? Can't tell at this point. If the two masses in the first equation, M and m, are in fact meant to be the same, then the second and third equations are just the solution of the first equation for v_B. I assume this is the case. That doesn't solve the "2L" question though.

The fourth equation looks like a momentum conservation: m1v1= (m1+m2) vB. If we assume that M = m = m₁ + m₂ then it suggests that two objects collided and stuck together. It looks like mass m₁ moving with a velocity v₁ hit a stationary mass m₂ and had a velocity v_B as a result. Then perhaps it rose a distance 2L. I therefore suggest the following problem is the one being solved:

A block of mass m₂ is hung from a rigid rod of length L that can pivot around one end. A bullet of mass m₁ is shot into the block. With what velocity must the bullet be going in order for the combined bullet and block have just enough energy to pivot around to the position vertically directly over the pivot.

This will naturally raise the combined objects a distance 2L solving the second labeling problem.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 8. November, 2005.