Problem

Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish

Linear Spaces of Functions

Last week we considered the set of functions consisting of the sum of the two functions sin θ and cos θ:

f(θ) = a sin θ + b cos θ.
.
where a and b are arbitrary complex numbers. We can associate this function with a vector

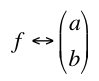
and we proved that this set of functions forms a linear space.
(a) From the usual definition of inner product in our vector space describing the motion of a single particle in one dimension, we might come up with one or more definitions of an inner product in this space. Construct one and show that it doesn't work -- that it doesn't give an inner product according to the definition given in class on Monday. Discuss why this is the case.
(b) Show that the definition

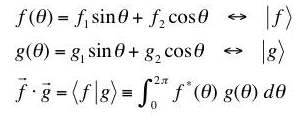
satisfies the conditions for an inner product.
(c) What is the dimension, n, of the inner product space constructed in parts (a) and (c)? Construct a set of n orthonormal vectors in this space that can serve as a basis.

Solution

(a) We might be tempted to just multiply the functions as our inner product since a function is just a number so it superficially looks like a 1-D space. For two vectors in 1-D we could just multiply them. But here, if we multiply

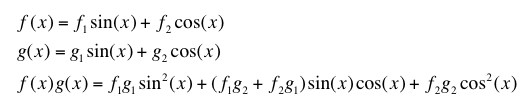
We don't in general get a number but a function. And it isn't even a function in our space, not having the right form! So just multiplying functions here isn't allowed. (We'll figure out what that means later.)

(b) The inner product defined here comes from thinking of our function not just as a number, but as an infinite set of numbers -- one for each given value of x. This is more like a many-dimensioned vector space. What we did in that case to take the inner product was to multiply together the two values that had the same index and add them together -- like this

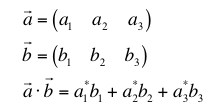
So with our f and g we multiply together the corresponding values for a given index label (here x) -- getting f^*(x) g(x) -- and add them all up. Here, since x is continuous, that means integrate. Let's see if this satisfies the conditions for an inner product.

It's linear in the vector variables (f and g).
If you scalar multiply either function, it comes out of the integral (with a * if it's on f).
It's complex symmetric.
The lengths are always positive.

and the only way it can equal 0 is if f = 0.

(c) The dimension of this space is 2 since there are only two linearly independent elements, sin θ and cos θ. Every element of this space can be written as a sum over these two.

To normalize them, we have to construct the integrals

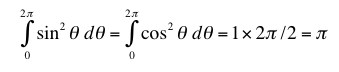
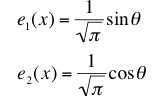
where to get these values we have used the "area trick", that is, the observation that over a full oscillation, the sin² and cos² functions are complementary, each covering 1/2 of the area (since sin² + cos² = 1 and they have the same shape, just shifted a quarter of an oscillation). This means our normalized functions are:

To see that they are orthogonal we just have to work out the overlap integral.

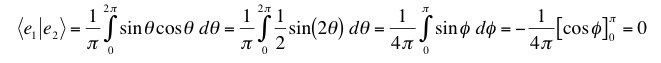
So they are orthogonal as well as normalized.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 8. November, 2005.