Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

Two identical wheeled carts of mass m are connected between two walls as shown in the figure below. The two outer springs have spring constants k and the inner spring has spring constant 2k. All three springs have a rest length l0 and the distance between the walls is L.

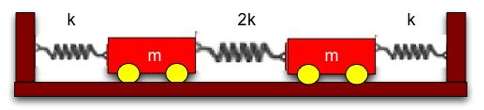(a) Guess the normal modes of this system without doing any calculations. Explain your reasoning making a physical, not a mathematical argument.

(b) Assuming that the modes you guessed for part (a) are correct, figure out what you think the frequency of each mode must be.

(c) Now carry out the explicit mathematical calculation of the modes and frequencies to determine whether your physical analysis is correct. Choose a convenient coordinate system for describing the positions of the carts and write the equations of motion for the carts. Find the normal modes and frequencies explicitly by solving these coupled differential equations.

(d) In writing your equations of motion, you probably ignored some factors or effects that are present in real systems, but that you expected to be small and therefore negligible. Identify 3 such factors. (Choose ones that you might want to include if you were trying to create a really accurate description of this physical system.)

Solution

(a)/(b) From the symmetry of the system (the system is symmetric about the midpoint: both carts have the same mass and the outside springs have the same spring constant), we might guess that there would be two normal modes:

• The masses move in the same direction with the same amplitude
• The masses move in the opposite direction with the same amplitude.

A "normal mode" means that both masses oscillate with the same frequency. Let's see why this works in each of the proposed modes.

The reason that we expect the first set of displacements to be a normal mode is that if the masses move in the same direction with the same amplitude, the central spring doesn't change the amount that it stretches. Therefore, it has no effect on either mass when it moves. The two masses both see the same restoring force from the outside spring they are connected to. Since they each feel the same force (same k) and have the same mass (same m) they should both have the same frequency [ω² = k/m = ω₀²].

The reason that we expect the second set of displacements to be a normal mode is that if the masses move in the opposite direction with the same amplitude, the central spring squeezes twice the amount that a single mass displaces. Therefore, it has the same effect on both masses when they move. The two masses both also see the same restoring force from the outside spring they are connected to. Since they each feel the same forces (same k) and have the same mass (same m) they should both have the same frequency [ω² = (k+2(2k))/m = 5ω₀²]

(c) We learned that it is useful to measure our coordinates from the equilibrium positions. If we take the displacements from equilibrium of the two masses to be y₁ and y₂, the equations of motion (Newton's second law for each mass) become:

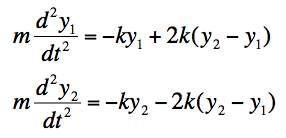
We can check the signs by considering what happens if y₁ is positive and y₂ is 0. Then the force from the first spring (spring constant k) on mass 1 should be in the negative direction as should the force on mass 1 from the second spring (spring constant 2k). These are both correct. The force on mass 2 should from the second spring should be in the positive direction and the force from the third spring (spring constant k) should be 0. This is correct. If y₁ is 0 and y₂ is positive, the force on the first mass from the first spring should be 0 and from the second spring should be positive. (Correct) The force on the second mass should be negative from the second spring (correct) and negative from the third spring (correct).

Now we can try the Ansatz that each oscillates like e^iωt. If we put

y_n = A_ne^iωt n = 1,2

our coupled ODEs turn into the matrix equations

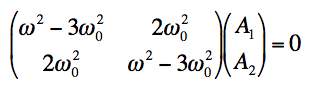
This is simplified if we factor out ω₀² and define λ = ω/ω₀. The resulting equations simplify to:

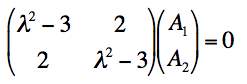
We know we can only get a non-0 solution if the determinant of the matrix vanishes. So we must require:

Since when the determinant is 0, both of our equations are the same, we can use the first to find the ratio A₁/A₂.

(λ²-3)A₁ + 2 A₂ = 0
(λ²-3)A₁ = -2A₂
A₁/A₂ = -2/(λ²-3)

For λ² = 1, the ratio is (-2)/(-2) = +1 so both amplitudes are the same.
For λ² = 5, the ratio is (-2)/(+2) = -1 so both amplitudes are the same magnitude but opposite direction.
These are the results we predicted.

(d) I would include the friction between the cart and the tracks, check to make sure that the springs were in their Hooke's law regimes for the entire range of stretching and compression they would encounter, and I would try to include some correction for the fact that the springs were not massless.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 28. October, 2005.