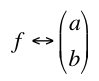Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

In our work in class so far we have used vector spaces to describe the position of objects in space, other physical quantities built from position such as velocity or momentum, and physical quantities that transformed in some way like position such as force or magnetic field. We have built up larger spaces by describing the motion of one particle in many dimensions or many particles (so far) in one dimension. As a result of these two different examples, we have created a mathematical abstractions -- a linear (vector) space -- that obeys certain properties. Once we have these properties, we can apply these ideas to other examples, effectively finding cases in which the analogy to motion of a particle in many dimensions (or of many particles in one dimension) is so good that we can use the same math. One example that will turn out to be of great importance, both in wave theory in elastic media and in quantum physics, is the case of functions. We'll begin by working out a simple example.

Consider the set of functions consisting of the sum of the two functions sin θ and cos θ:

f(θ) = a sin θ + b cos θ.

.

where a and b are arbitrary complex numbers. We can associate this function with a vector

Prove that this set of functions forms a linear space according to the definition of a linear space given in class.

Solution

In order for a set of objects to be a linear space, you have to be able to define the sum of the objects and the scalar multiplication with a number (either real or complex). The usual rule for adding functions -- that is, you add the values point by point -- and for multiplying a function by a constant work here.

The left hand sides of these equations may seem a bit strange. What we mean by "(f + g)(x)" is "the function we associate with the linear space sum of two function f and g" and what we mean by "(af)(x)" is "the function we associate with the scalar multiple of the function g by a constant (scalar) a".

Once we know what we mean by the sum and scalar multiple of a function in our space, it is very straightforward to prove all the required properties.

• The sum of two elements of the space is an element. (f(x) + g(x) is the sum of a sine + a cosine if both f and g have that form.)
• The 0 function works as the identity vector.
• For any function in the space, f(x), the function -f(x) works as an additive inverse.
• For any complex number z and element of our space f(x) = a sin θ + b cos θ, the function (zf)(x) = (za) sin θ + (zb) cos θ is in our space.
• Multiplication by 1 serves as an identity for scalar multiplication.
• For every complex z ≠ 0, multiplication by 1/z serves as a multiplicative inverse.
• Distribution is inherited (follows directly) from the distribution of addition and multiplication of numbers and functions.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 28. October, 2005.