
Teaching Physics with the Physics Suite
Edward F. Redish
 |
Teaching Physics with the Physics Suite Edward F. Redish |
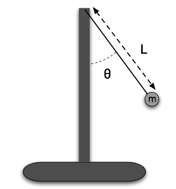
Some of the graphs shown below represent the motion of a pendulum -- a massive ball attached to a rigid, nearly massless rod, which in turn is attached to a rigid, nearly frictionless pivot.
On the right below are shown four graphs of the pendulum's angle as a function of time. On the left are a set of four initial conditions and a denial. Match each graph with its most likely initial conditions (or with the denial). Note that the scales on the y axes are not necessarily the same. (There is not necessarily a one-to-one match.)
| (1) θ0 = 120o ω0 = 0
(2) θ0 = 173o ω0 = 30o/s (3) θ0 = 6o ω0 = 0 (4) θ0 = 173o ω0 = 0 (5) Not a possible pendulum graph. |
(A) 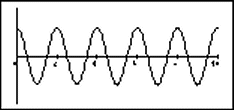 (B) (B) 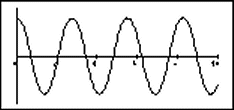
(C) |
Solution
| The answers are as follows: (1)-B, (2)-D, (3)-A, (4)-C.
We can derive the equations of motion for the pendulum for all angles from the relation between angular acceleration and torque (I dω/dt = τ). The result is:
For small angles, we can approximate sin θ ~ θ so the equations reduce to that of a simple harmonic oscillator with angular frequency ω02 = g/L. As the angle gets larger, the torque gets smaller than the linear approximation would suggest since sin θ < θ and dramatically so after 90o when the sine curve begins to turn down but the linear approximation keeps going up. |
 |
The result is that we would expect it to continue to oscillate but more slowly once the sin θ gets significantly less than θ (at above about 60o). As it approaches close to the top, we would expect it to really slow down, almost hanging up near the top since the force of gravity is now mostly pushing the bob down onto the rod. Very little of it is effective in accelerating it to go downward. This explains what is happening in figures (A), (B), and (C).
If we are near to the top and have a positive velocity, it will go "over the top." It will then have enough energy (ignoring friction or other damping) to keep going around and around. This is what is happening in figure (D).
Page last modified October 21, 2005: O10