
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for |
When we think about a line integral, we can imagine doing it by our fundamental definition of the integral: breaking it up into small bits and summing the result. For a line integral to construct a potential energy, is we broke up our path into N segments dri centered on positions ri our approximation to a line integral might look something like this.
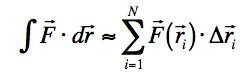
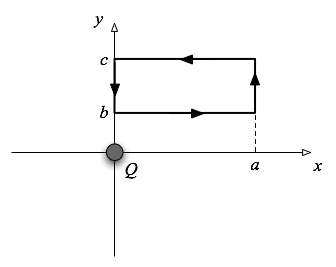
Consider the situation in which a charge Q is at the orgin of our coordinate system in 2D. We wish to calculate the electrostatic potential around the loop shown in the figure at the right.
Write the loop integral
as the sum of four simple integrals in either x or y, putting in explicit expressions for the electric field and the vector displacements so that each of your integrals are simple (no vectors) integrals of a function of x and y over dx or dy. (Hint: It may be convenient at first to express some of your expressions using polar variables, r and θ. But in the end, make sure everything is expressed in terms of x and y with explicit values substituted in for variables wherever possible.) If you can, do the integrals analytically. What result did you expect to get for the sum of the four integrals? Did it work the way you expected? If not, explain what went wrong, either with your expectations or with your calculations. |
 |
Solution
The Electric field from a point source can be expressed as:
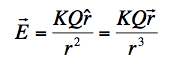
I choose to write with the vector distance rather than with the unit vector since we will be taking dot products and it is a bit easire to keep track.
Starting at the lower left corner of the loop, the point (x,y)=(0,b), we will consider the four legs of the loop:
We will have to be careful in doing these, since the "flow" around the loop tends to make us look at each step in the direction indicated. We will have to figure out how to do the integration so as not to "double count" any minus signs.
Our first leg of the integral is evaluated as follows:
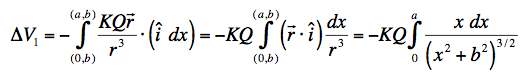
This reduces to a standard integral:
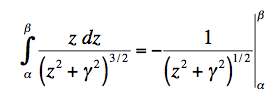 .
.
(We can easily see that this is correct by differentiating the right hand side with respect to z.) Putting in the appropriate values gives:
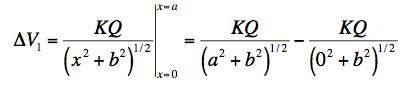
Doing the other three legs similarly, we get:
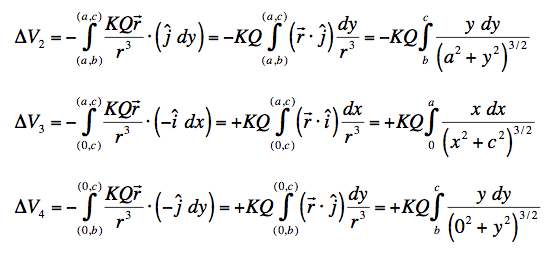 .
.
The last two are a bit tricky because of the signs. Why do these have negative signs while the first two have a positive sign? Notice that in the first of the integrals in each of the expressions I have integrated from the lower value of the integrand to the upper -- always -- even when the arrow is pointing in the other direction (as it is on legs 3 and 4). Also in those legs I have chosen to exress the dr vector with a negative sign. One could drop the negative sign and run the integral in the other direction, but this way seems clearer to me as one can get it from "digging down to the roots of meaning" of the integral. That is, if you express the integral of the dot product of E and dr as a sum over steps, it is clear that any negative signs come from whether the dot product is positive or negative: that is, whether E and dr are in the same or opposite direction. By taking the correct sign for the vectors E and dr, we are able to guarantee that we can then just add them up -- that is, integrate them directly without introducing a negative sign -- and we will get the right sign.
The results for the four integrations are then:
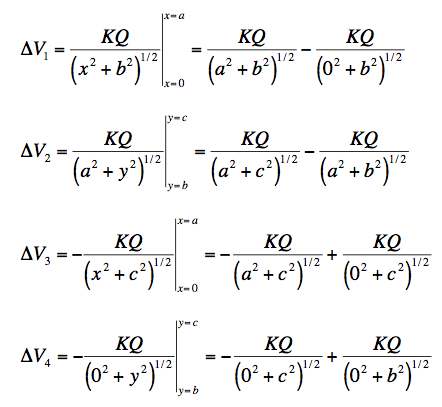
It is clear that the "leading" endpoint of one integral cancels against the "trailing" endpoint of the next, just as in the derivation of the fundamental theorem of calculus done in class. Since we have a loop, everything cancels and we get a result of 0.
This is exactly what I expected. Since I know that the static electric force can be derived as the gradient of a potential, the fundamental theorem of calculus should tell us that the integral along a line should be the potential evaluated on the boundary of the line -- potential at the final point minus potential at the initial point. Since the initial and final points are the same, the result should be 0 -- and it is.
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 5. October, 2005.