Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

When we were considering the kind of resistance a fluid can exert on an object moving in it, we considered the force linear in velocity, the viscous force. In fluid flow, the viscosity is a kind of internal friction. If we consider two neighboring sheets of fluid (don’t worry too much about how to define this precisely) moving with different velocities as in the figure at the right, then each sheet will exert a force on the other of magnitude

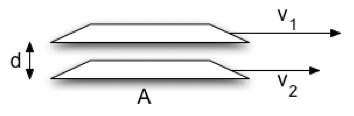where A is the area of the sheets Δv the difference between their velocities, and d the distance between them. The constant η is known as the viscosity. If you have a fluid of density ρ flowing through a pipe of diameter D, you can create a natural velocity for the system from ρ, D, and η. Find it using dimensional analysis.

Solution

The dimensions of the density and the diameter are easy to find.

[ρ] = M/L³

[D] = L

but we have to figure out the dimensions of η from the force equation:

.

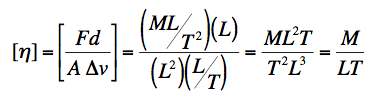To get rid of the M, we have to divide η by ρ giving

.

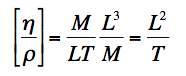Now we need to get rid of the extra length, so if we divide by D we have a natural velocity (I call it v_η since it is associated with η):

.

RETURNS

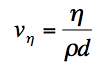University of Maryland	Physics Department	Physics 374 Home

Last revision 4. October, 2005.