Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

1. Write the exact solutions for y(t) and v(t) at the time t_n = n Δt.

2. Write the Euler approximation for N2 as a stepping rule for getting y_n+1 = y(t_n+1) and v_n+1 = v(t_n+1) if you know y_n and v_n.

3. Starting from (y₀, v₀) = (0, 0), use the Euler rule to find the first three steps, (y₁, v₁), (y₂, v₂), and (y₃, v₃). Can you generalize your result and make a conjecture for the answer for the n-th step? Can you prove that this is correct? (Hint: Try substituting your conjecture into the equation for (b).)

4. How bad is the answer? Does it get better at time gets longer? or worse? Discuss why you think it does what it does.

Solution

a. The equation of motion, a = F^net/m, immediately reduces to a = dv/dt = -g in this case. Therefore, the exact solution for v(t) is

v(t) = C - gt.

where C is a constant of integration. The initial condition is v(0) = 0 so the constant is 0.

v(t) = -gt.

This gives the next equation, dy/dt = v = -gt. Integrating this quickly gives the exact solution for y(t):

y(t) = B - ½ gt²

where B is a constant of integration. Since we also start with y(0) = 0, the exact solution for y is:

y(t) = - ½ gt²

So putting in the values requested, we get the exact solutions:

v_n = v(t_n) = -ngΔt.

y_n = y(t_n) = - ½ n²gΔt² .

b. The Euler method can be written as a stepping rule:

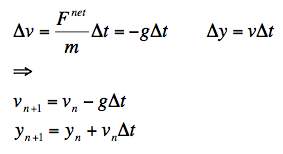
If we know v_n and y_n we can calculate v_n+1 and y_n+1.

c. Using the stepping rules and starting with (0,0) for (y₀, v₀), we get the following results:

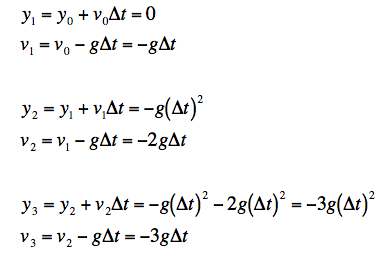
It's easy to generalize the result for v. We are just getting v_n = -ng Δt. If we put this into the right side of the stepping rule for v_n, we get the same conjectured results for v_n+1. This proves that the conjecture is correct. And furthermore, this is the exact answer so for the velocity in this example, the Euler method is perfect.

It's a bit harder to see what's going on for y. It is always proportional to -g(Δt² (as it has to be by dimensional analysis). The coefficients for n=1,2,3 are 0,1,3. It's hard to see what this sequence is. We could generate a few more steps, but since we know the exact v generated by Euler, let's put that into the stepping rule for y to see what we get.

y_n+1 = y_n - ng (Δt)²

so y_n+1 is -g (Δ t)² times the sum of the integers from 1 to n. This sum is well known and you probably saw it in high school. If you don't remember it, the result is:

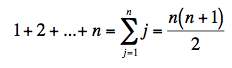
This result is pretty easy to prove. Write A_n = 1 + 2 + ... + n. Then it's easy to see that A_n is defined byt the stepping rule A_n+1=A_n+(n+1). Just substitude the conjecture, A_n = (n+1)n/2, in for A_n and A_n+1 and see that it works. (It's a bit harder to come up with the form. I was able to do it by generating the results for a set of numbers up to 6 and observing that it appeared to be true that A_n+1=n²-A_n. Adding the two together gave me the result.)

d. As we have seen, the answer for the velocity is exact. The answer for the position isn't bad. The leading term -- the one proportional to n² -- is exact. But there is an error that goes like n/2. This is an interesting kind of error. As a fraction of the exact answer it falls (n/n²=1/n) but the absolute error increases with every step. It does this because the stepping rule keeps adding in the initial value. Since the position couldn't get started in the first step since the initial velocity was zero, the growing of the position with time is off a a step. So we sort of see the n-1 step where we should see the n-th.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 16. September, 2004.