Problem

Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish

Falling in a viscous medium

When a small object moves in a viscous medium it experiences a resistive force that is opposite in direction to its velocity and directly proportional to its speed. For this problem, assume that the object only moves up and down and take the upward direction to be positive. We write the viscous drag force as F_v = -bv. In this problem, you will solve the differential equation for the motion in one (vertical) dimension of a body subject to gravity and viscous drag.

What are the dimensions of the viscous drag coefficient, b?
Write Newton's Second law of motion for a body falling under the influence of gravity and viscous drag.
From the parameters of the equation (m, b, and g) create a natural mass scale, M_N, a natural length scale, L_N, and a natural time scale, T_N.
From your natural length and time scales, create a natural velocity scale, V_N = L_N/T_N. Interpret what this velocity means physically.
Write Newton's second law as a differential equation for the velocity, v, and re-express it as an equation for a dimensionless velocity, V = v/V_N as a function of a dimensionless time, T = t/T_N. If you simplify the resulting equation, all the parameters of the problem should drop out and each of the terms should be dimensionless.
Solve this equation using standard techniques for first order equations.
If the particular solution to your first-order differential equation satisfies the initial condition, V(T=0) = v₀/V_N (that is, the initial velocity is v₀) eliminate your integration constant in favor of v₀. Rewrite your solution in terms of dimensioned variables and group your terms in a way that you can clearly explain what your solution is telling you about how the motion of the objects evolves. Give a clear and quantitative (in symbols, not in numbers!) description of what the object does as a function of time.

Solution

(a) The viscous drag coefficient, b, when multiplied by a speed, v, gives a quantity with dimensions of force. Therefore, b must have the same dimensions as force/velocity.

[b] = [F/v] = (ML/T²) / (L/T) = M/T.

(b)

a = F^net/m

dv/dt = (1/m) (-mg - bv)

dv/dt = -g - (b/m) v.

(c) We have three parameters with the following dimensions: [m] = M, [g] = L/T², [b] = M/T. When we multiply these together with arbitrary powers, we get a quantity with the following dimensions.

If we want a quantity with a dimension of mass, we need to choose the equations

x+z = 1
y = 0
-2y-z = 0

This has the obvious solution y=0 ⇒ z=0 ⇒ x=1 so our quantity for mass is just m. (This one was obvious.)

M_N = m

If we want a quantity with a dimension of length, we need to choose the equations

x+z = 0
y = 1
-2y-z = 0

These have the (less obvious) solution y=1 ⇒ z=-2 ⇒ x=2 so we get:

L_N = gm²/b².

If we want a quantity with a dimension of time, we need to choose the equations

x+z = 0
y = 0
-2y-z = 1

These have the solution y=0 ⇒ z=-1 ⇒ x=1 so we get:

T_N = m/b.

(d) The natural velocity is just the ratio:

V_N=L_NT_N = (gm²/b²)/(m/b) = mg/b

To see what this means physically, we note that

mg = bV_N

When this happens, we note that the net force vanishes. At this velocity, the force of air resistance is exactly equal to that of gravity. If the velocity were in the same direction as gravity, the forces would cancel and the object would continue at that velocity without change. This velocity is therefore the terminal speed. (What happens if the object is going upward with this speed?)

(e) We begin by replacing the dimensioned variables, v and t by their dimensionless counterparts. We then express the natural velocity and time in terms of the problems parameters and simplify. In the end, all the parameters cancel out and we are left with a dimensionless equation.

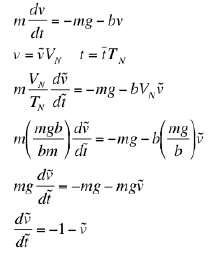
(f) To solve this, we separate variables and integrate.

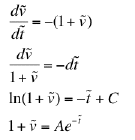
Here, we have express the exponential of the integration constant, C, as A. Since C is arbitrary (i.e., unknown at this point) it doesn't matter.

(g) Solving for the particular value of the constant A when the initial velocity is known, we can then find the particular solution, go back to the dimensioned form, and regroup for purposes of interpretation.

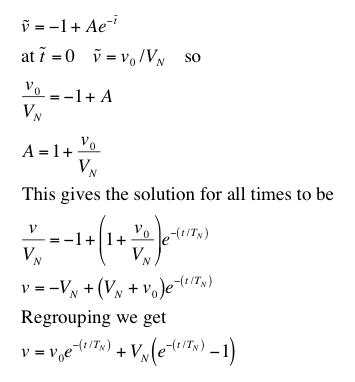
We can see that this solution makes sense. Initially, at t = 0, the exponentials become 1, so the first term is just v₀ and the second term vanishes. As time gets large, the exponentials become 0, so the first term vanishes and the second term becomes -V_N, the natural (=terminal) velocity in the downward direction. Notice this happens whether you throw the object up initially (v₀ > 0), down initially (v₀ < 0), or just drop it (v₀ = 0).

RETURNS

University of Maryland	Physics Department	Physics 374 Home

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 16. September, 2004.