Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

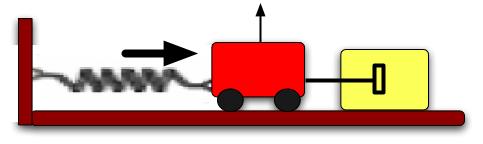
A small cart of mass m with (nearly) frictionless wheels is connected to a spring of spring constant k. It is connected to a plunger imbedded in light oil as shown in the figure at the right. The oil provides a damping force of -bv. The cart is struck at time t = 0 by a quick tap with a hammer. We'll model this system by the equation of motion

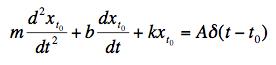
(a) What are the dimensions of the constant A?

(b) Assuming that the cart is initially at x = 0 and is at rest, use the Fourier transform to solve for x_t0(t),the position of the cart as a function of time when it is struck at a time t₀.

(c) Show that for a general function, f(t), we can write

.

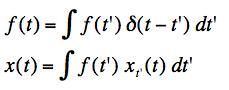Show why this works, starting from the equation given above part (a). (You don't have to show that the solutions agree.)

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 12. December, 2005.