Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

An electromagnetic plane wave moving in the z direction can be written as (the real part of)

From Maxwell's equations in free space, we can show that the amplitude vector, E₀, has to be perpendicular to the direction of propagation and therefore lie in the the x-y plane. We could therefore treat the amplitude vector as a two-dimensional vector in a complex linear space:

.

(a) If both E_0x and E_0y are real numbers (with dimensions of force/charge), find the electric field vector at the origin (i.e., (x,y,z)=(0,0,0)) as a function of time. What is it's magnitude and direction as a function of time? (Hint: Remember that the physical electric field is the real part of the complex expression.)

(b) Suppose both E_0x and E_0y are complex numbers with the same phase, that is,

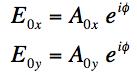
where A_0x and A_0y are both real (but not necessarily equal) and the φ in both terms is real (and they are both the same number). How does your result from part (a) change?

(c) Now suppose that instead of having the same phase, they are 90^o out of phase. That is, suppose that:

.

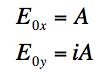Find the electric field vector at the origin as a function of time. Describe how it is changing.

(d) We can consider two distinct bases for the linear space of these 2-D E fields, {|e₁>, |e₂>} and {|+>, |->}, where:

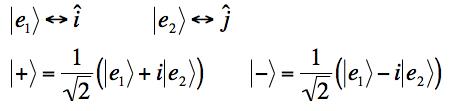
We can express any E-field vector in one of the two ways:

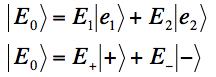
Explain what each of the coordinates E₁, E₂, E₊, E_- mean and express {E₊,E_-} in term of {E₁,E₂}.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 28. November, 2005.