Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

(a) When calculating the derivative of a function as an approximation numercially, it is convenient to express the derivative in a symmetric way:

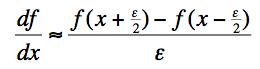
The derivative is defined as the limit of the right hand side above as ε approaches 0. Demonstrate that this is correct to O(ε²) using the Taylor series and show what it means graphically in terms of the slope of the tangent to the curve.

(b) The integral of the function f is defined as the limit of the Riemann sum:

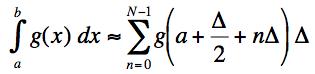
where Δ = (b-a)/N. The integral is defined as the limit of the right hand side above as N approaches infinity. Give a graphical interpretation of this result explaining why the argument of the g on the right is what it is.

(c) Combine these two results by considering the integral of the function

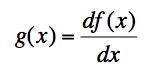
and using the approximation for the derivative with ε = Δ. Demonstrate the result (the fundamental theorem of calculus)

.

RETURNS

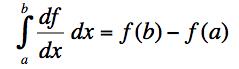University of Maryland	Physics Department	Physics 374 Home

Last revision 28. November, 2005.