Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

Consider two masses connected to each other and to two rigid walls by three identical springs. We make the following approximations:   the springs are massless and have a rest length l0 <L/3 we can ignore gravity the masses only move in the up-down ("y") directions when the masses are in their equilibrium (horizontal) position, the springs are under a tension T.

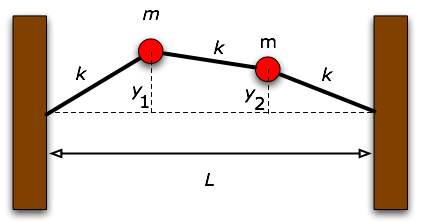(a) For an arbitrary pair of displacements y₁ and y₂ find the net forces acting on each of the masses and write Newton's second law for each mass.

(b) Assume both displacements remain very small compared to L so that terms of the the order of (y/L)² can be ignored compared to first order terms. Show that the equations of motion reduce to equations very similar to the ones we derived for longitudinally moving masses but with an effective k. Express k_effective in terms of the parameters of the problem: T, m, l₀, and L.

(c) Without solving the problem mathematically, describe what you think the normal modes will look like and what their frequencies might be.

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 7. November, 2005.