Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

Two identical wheeled carts of mass m are connected between two walls as shown in the figure below. The two outer springs have spring constants k and the inner spring has spring constant 2k. All three springs have a rest length l0 and the distance between the walls is L.

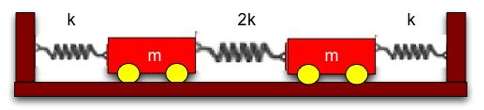(a) Guess the normal modes of this system without doing any calculations. Explain your reasoning making a physical, not a mathematical argument.

(b) Assuming that the modes you guessed for part (a) are correct, figure out what you think the frequency of each mode must be.

(c) Now carry out the explicit mathematical calculation of the modes and frequencies to determine whether your physical analysis is correct. Choose a convenient coordinate system for describing the positions of the carts and write the equations of motion for the carts. Find the normal modes and frequencies explicitly by solving these coupled differential equations.

(d) In writing your equations of motion, you probably ignored some factors or effects that are present in real systems, but that you expected to be small and therefore negligible. Identify 3 such factors. (Choose ones that you might want to include if you were trying to create a really accurate description of this physical system.)

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 21. October, 2005.