
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for |
When we think about a line integral, we can imagine doing it by our fundamental definition of the integral: breaking it up into small bits and summing the result. For a line integral to construct a potential energy, is we broke up our path into N segments dri centered on positions ri our approximation to a line integral might look something like this.
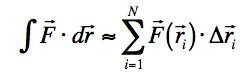
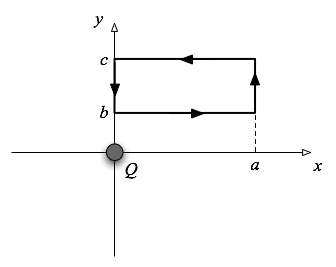
Consider the situation in which a charge Q is at the orgin of our coordinate system in 2D. We wish to calculate the electrostatic potential around the loop shown in the figure at the right. Write the loop integral
as the sum of four simple integrals in either x or y, putting in explicit expressions for the electric field and the vector displacements so that each of your integrals are simple (no vectors) integrals of a function of x and y over dx or dy. (Hint: It may be convenient at first to express some of your expressions using polar variables, r and θ. But in the end, make sure everything is expressed in terms of x and y with explicit values substituted in for variables wherever possible.) If you can, do the integrals analytically. What result did you expect to get for the sum of the four integrals? Did it work the way you expected? If not, explain what went wrong, either with your expectations or with your calculations. |
 |
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 30. September, 2005.