Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

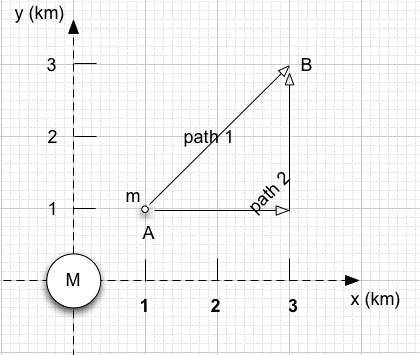
Gravity is one example of a conservative force. That is, the work done by the force of gravity on an object that moves from point A to point B should be independent of the path chosen between A and B. This problem will investigate that claim and give you practice in evaluating line integrals. A rocket is taken from a point A near an asteroid to another point B. We will consider two (unrealistic) paths labelled path 1 and path 2 as shown in the figure. Calculate the work done by the asteroid on the rocket on each path. Use the full form of Newton's Universal law of gravitation (not the flat-earth approximation "mg"). Calculate the work done by using the fundamental definition of the work

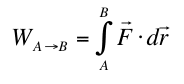not by using potential energy. (We are trying to demonstrate that it's OK to use PE for gravity. Using it here would defeat the point of the problem.)

Depending on how you set up your integrals, Mathematica may or may not be helpful. Feel free to use it if you choose (though it is not necessary for the calculations required).

(Problem by T. Bing)

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 1. October, 2004.