Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

The diffusion equation: can be used to describe many things, from the spreading out of perfume molecules from an open bottle, to the flow of heat, to the propagation of electrons (the last if D is taken to be complex). Consider the temperature of a large but thin plate of material imbedded in a heat bath. Treat this as a uniform 1-D system (ignoring the spatial variation of T in the y and z directions of the plate) with ψ = T(x,t), the temperature in the interior of the slab as a function of distance and time. We can rescale our thermometer for convenience to choose the temeperature of the heat bath as 0. A moment after its imbedding into the heat bath, the slab has a teperature T0 in its interior, falling precipitously to 0 at its edges as shown in the graph at the right.

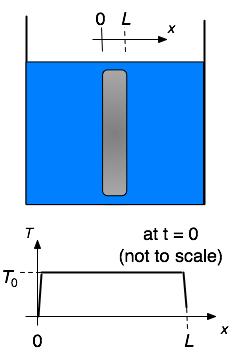(a) Assume that the time and space dependence of T(x,t) can be separated, T(x,t) = f(x)g(t) and use a separation constant to obtain ordinary differential equations for f and g.

(b) Use a physical argument to choose the sign of your separation constant as it appears in the time equation and solve the equation.

(c) Find the general solution to the space equation given the boundary conditions, T(0,t) = 0 and T(L,t) = 0 for all t.

(d) Explain how you would go about finding T(x,t) for t > 0 and write equations that would allow you to calculate that function if you had a computer available.

Solution

(a) Putting the separated solution in and dividing both sides of the equation by T gives

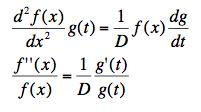
Since this says that a function of x is equal to a function of t they both have to equal a constant. (Fix t and vary x. This shows that f''/f is a constant independent of x. Fix x and vary t. This shows that g'/g is a constant independent of t.) Write it as

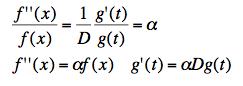
These are orginary differential equations for f and for g.

[Grading: 3 pts for the space equation, 2 for the time.]

(b) If we put a slab of hot metal into a water bath we expect it to cool down. In particular, as t goes to infinity, we expect our temperature to become uniform and constant. The equation for g(t) is a standard equation for an exponential. The solution will look like exp(αDt). Since D is positive, if we want the result not to blow up (go to infinity and keep changing as t gets larger) we will have to take alpha as negative. Write it as α = -k² to make sure we don't forget. This makes our equations into:

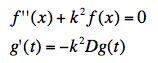
[Grading: 2 for sign, 3 for reason]

(c) The equation for f is very familiar. It it the same as for the string and we even have the same boundary conditions. A solution is

The boundary condition at 0 requires that B=0 and the boundary condition at L requires that kL = nπ so the general solution is

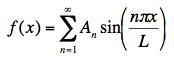
[Grading: 2 for the sin and cos solutions, 2 for eliminating the cos terms, 3 for finding the appropriate values of k, and 3 for generating the general solution. If k is not related to the separation constant, -1]

(d) Each term with a k_n has a specified α_n = -k_n² and it produces a time dependence exp(-k_n²Dt). If we have expanded our starting shape (which here is basically = a constant) in terms of the solutions of the diffusion equation like in (c), then our time dependence will be

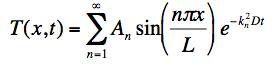
We just have to find the coefficients A_n as f_n -- the coefficients that appear if we use instead of just the sin terms, the sin terms with a constant included to make them orthogonormal as in the string case:

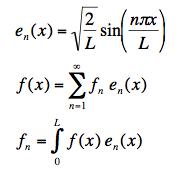
[Grading: 4 for the expansion of the function giving the initial shape, 3 for putting in the time correctly, 3 for showing how to get the coefficients.]

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 12. December, 2005.