Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

In this class we have discussed a number of different linear inner product spaces. One of the properties of a linear inner product space is that you can create a basis that provides a complete set. Explain what a basis is, state the completeness relation for the basis and give two examples of linear inner product spaces. Note: This is an essay question. Your answer will be judged not solely on its correctness, but for its depth, coherence, and clarity.

Solution

A basis is usually a subset of vectors from the space (though sometimes, the elements of our basis or pseudobasis do not become members of the space until multiplied by something)*. The defining characteristic is that the set is linearly independent -- no vector in the set can be written as a sum of the products of the others with scalars -- and that it is complete. Completeness means that any vector in the space can be written as a sum of the products of the elements of the basis with scalars --like this:

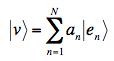
where the |e_n> are the set of basis vectors and the an are the coordinates of the vector |v> in the e-basis. The number N is the maximum number of linearly independent vectors we can have in the space and is the number of elements that must be in a basis. (For some spaces, N can be infinite and the sum might be replaced by an integral.)

The fact that a basis is complete can be expressed as the completeness relation

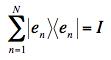
where I is the identity operator. Multiplying this times any vector |v> expresses it as a sum over the elements of the basis and identifies an as equal to <en|v>.

A linear inner product space must both have the linear addition and scalar multiplication properties associated with any linear space and an inner product defined that allows us to talk about lengths and angles. We have defined many such spaces. Two are: the ordinary Cartesian 3-D space that defines positions, and the set of all functions on a line segment that vanish on the endpoints.

* Even our usual i, j, k basis vectors are not members of the position vector space. They have the wrong units and have to be multiplied by a dimensioned coordinate in order to yield a vector in the space. We also use pseudobasis elements such as |x> or |k> in discussing the space of square integrable functions. Neither of them corresponds to such a function and therefore is not in the space.

[Grading: +3 for an explanation of a basis, +3 for a discussion of completeness, preferably with the completeness relation (though that was not required). +2 for each of two examples.]

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 12. December, 2005.