
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for Edward F. Redish |
| When visiting my daughter's family last Thanksgiving, I took the photo shown on the right of my six-year old grandson playing a harp. The string he is plucking is middle C ( f = 256 Hz, ω = 2πf). Their packet of extra strings said that string (made of nylon) has a diameter of 0.055 in. We dropped the extra string in a jar of water and it slowly sank to the bottom. Estimate the tension to which the string had to be tuned in order for it to correctly produce middle C when plucked. Be sure to clearly state your assumptions and how you came to the numbers you estimated, since grading will be mostly based on your reasoning, not on your answer. |  |
Solution
The frequencies of a taut string are the normal modes, with the dominant frequency excited being the n=1 state. The frequencies are determined by the speed of signals on the string, v0, and that speed is determined by the tension and the linear density. The equations determining the frequency f are:
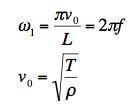
Solving for T gives
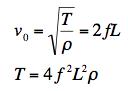
We are given the frequency, so we only have to estimate the length of the string and its mass density per unit length.
The length can be estimated by looking at the seated child. At age 6, we may estimate his height at being a bit less than 1 meter. The harp is almost as tall as he is, but the string he is plucking is in the middle of the harp, about half its height. So a reasonable estimate is about 0.5 m. (We could do better, but this is good enough for an estimate.)
Estimating the mass per unit length is a bit trickier. We are told it sinks slowly, so it is a bit denser than water -- about 103 kg/m3. But we want the mass per unit length. We know the diameter of the string, so we can calculate the volume and therefore the mass of a meter of string. The diameter is 0.055 in = (0.055 in)x(2.54 cm/in) ~ 0.15 cm = 1.5 x 10-3 m so the radius is about 0.75 x 10-3 m. Therefore we can calculate the volume of a one meter length of string, the mass of a meter of string, and ρ:
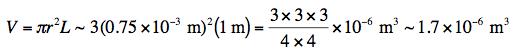
The mass is therefore about 1.7 x 10-6 kg for a 1 m length, and the density is about
ρ ~ 1.7 x 10-6 kg/m.
Putting this into the equation for the tension gives the result
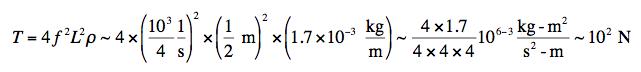 .
.
About 100 N -- equivalent to about 20 pounds. That seems reasonable.
[Grading: +6 for generating the equations to find T given quantities that can be estimated. One can also us λf = v0 and the equation for v0 in terms of T and ρ. Partial credit is given for some of the needed equations. +4 for estimating the density of the string. +2 for a decent estimate of the length. +3 for the calculation. As usual, a point is deducted if there is no discussion of how the estimation is chosen and a point is deducted for too many sig figs.]
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 12. December, 2005.