Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

A two mass system where each mass can be displaced in one dimension is described as a linear space spanned by the basis vectors

.

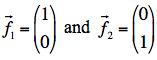Suppose the normal modes of the system are found to be described by the orthonormal set of vectors

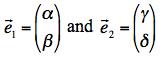
where α, β, γ, and δ could be complex.

(a) If we choose to describe these 4 vectors as Dirac states, |f_i>, i = 1,2 and |e_i>, i = 1,2, find the 8 inner products <e_i|f_i> and <f_i|e_i>.

(b) What is the matrix (in the f-basis) that represents the sum ?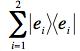

(c) A vector is represented in the f-basis by the sum 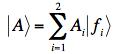. This same vector is represented in the e-bases by 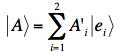. Find the A'_i in terms of the A_j.

Solution

(a) The dot products are easily obtained if one recalls that

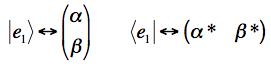
that is, when one takes the transpose of a complex vector from a ket to a bra, it corresponds to taking the complex conjugate.

The results are

.

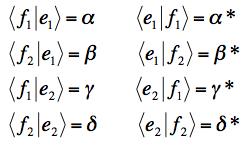[Grading: +2 for each of the answers. -2 if you forgot the *]

(b) The result is the identity matrix in any orthonormal basis. One was not required to prove this, but if you construct the outer product the result is:

.

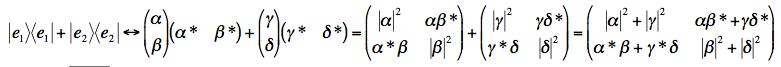To see that this is in fact the identity matrix, you have to use orthonormality of the basis vectors:

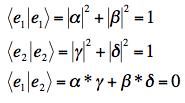
A little manipulation shown that the matrix is the identity.

[Grading: 5 pts for the identity matrix; 4 is the correct outer product is given but not recognized as I.]

(c) We equate the two sums since they represent the same vector. Dotting it with <e₁| picks out A₁' and gives an equation for it. Similarly, dotting with <e₂| picks out A₂' and gives an equation for it. The results are:

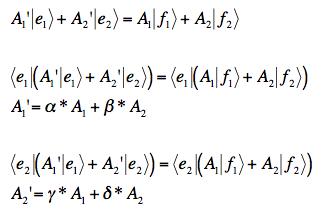
[Grading: +3 for knowing how to pick out the A' terms, +4 for getting the results. If you forgot the * in (a) no points were deducted for not putting it here.]

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 12. December, 2005.