
Problems for
Intermediate Methods in Theoretical Physics
Edward F. Redish
 |
Problems for Edward F. Redish |
Two identical wheeled carts of mass m are connected between two walls as shown in the figure below. The inner spring has spring constant k and the two outer springs have spring constants K = 10k. All three springs have a rest length l0 and the distance between the walls is L.
|
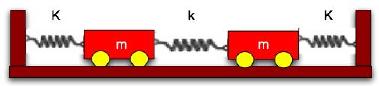 |
(a) Choose a convenient coordinate system for describing the positions of the carts and write the equations of motion for the carts. Be sure to specify your coordinate system.
(b) Describe what the normal modes will be like.
(c) Find the normal modes and normal frequencies (expressed as a function
of ![]() ) using any approach you
want.
) using any approach you
want.
Solution
(a) The most convenient coordinates are the ones that measure the positions of the carts taking the 0 to be at their equilibrium position. When this is done, the tensions in the springs all balance and there is no net force on either cart when they are at their equilibrium positions. Any deviations from these positions produce additional forces from the springs proportional to the displacements (assuming the springs remain in their Hooke's law regime).
The equations of motion are simply ma = Fnet for each mass.
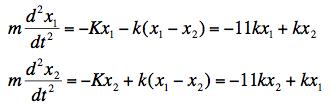 .
.
[Grading: specification of coordinates +2, two F=ma equations +2, correct treatment of K springs +2, correct form for k spring +2, correct signs for k spring +2]
(b) The system is symmetric about the center, and there are two masses, so we expect there to be two normal modes. In the first (and lower frequency), the masses will both move with the same amplitude in the same direction. In the second (and higher frequency), the masses will both move with the same amplitude, but in the opposite direction. These will be normal modes since in each case, both masses feel the same magnitude of restoring forces at the same time, so they will change their velocities in the same way.
[For one correct mode +3, for second correct mode +2]
(c) The easiest way to find the normal modes and frequencies are using physical arguments. In the two normal modes, which we described in (b), the system will have the initial displacements:
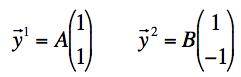
In each of these modes we can find the frequencies by considering one of the masses. In the first mode for the left mass, the motion produces extra pulls from the left-most spring only. The middle spring has no extra squeeze or stretch compared to its equilibrium position. As a result, it looks like a standard single-spring angular frequency, ω12 = K/m. In the second mode for the left mass, the motion produces extra pull from the left-most spring but also a double squeeze of the center spring. The result is an angular frequency ω22 = (K+2k)/m or
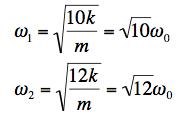 .
.
There are other ways to do this. A nice way developed during the exam by one student is to use the first equation of motion and replace x1=x2=x for the first mode and x1=-x2=x for the second mode. These yield the results immediately. One can, of course, also take the ansatz xn = An eiωt, obtain matrix equations, take the determinant, and find the eigenvalues and eigenvectors. This is a bit more difficult and time consuming.
[Grading: Correct specification of modes -- algebraic description and association with correct frequencies +5, frequencies for modes +5 (= +2+2+1 for each mode and a reason)]
| University of Maryland | Physics Department | Physics 374 Home |
|---|---|---|
 |
 |
 |
Last revision 12. December, 2005.