Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

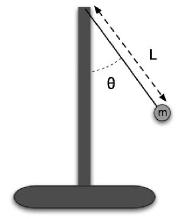
Consider a mass, m , connected to a heavy rigid stand through a light (mass << m) but rigid rod as shown in the figure at the right. The motion of this mass is governed by the angular, motion form of Newton's second law, I dω/dt = τ, where I is the moment of inertia, τ is the torque, and ω is the angular velocity. This yields to the equations: (a) If the pendulum is started at t = 0 with θ(0) = θ0 and ω(0) = 0, use the Euler method to approximately find the angle of the bob at times tn = n Δt for n = 1, and 2, assuming Δt is small.

(b) In asking part (a), we said, "assuming Δt is small."   Compared to what?   Explain your choice.

(c) Commonly we make the approximation sin(θ) ≈ θ so that the equations become the same as that for the simple harmonic oscillator.   Use the Taylor series to estimate how big θ must be before this approximation is off by 10%.

Solution

(a) The Euler method says to step into the future, make a Taylor series expansion around the present and keep up to first order (onlt the first derivative term). Use the equations of motion to evaluate the first derivative in terms of the data at the present. Since we are working with Newton's second law, our equations of motion are a pair of coupled first order equations:

where we have written g/L = ω₀². All the functions in both of these equations are evaluated at the time t ("the present").

If we want to step into the future, we need to use a Taylor series.

Dropping the second order term and putting in Newton's law for the derivative of θ, we get

As we step forward, we will need to evaluate at future times, so we need to write the Euler stepping rule for that as well.

So taking the pair of Euler method equations, we can make two steps into the future.

(The last line was not asked for in the problem but it would be needed if we wanted to step further into the future.)

(b) The time step Δt always has to occur in the Taylor series together with a constant that makes it unitless. We can easily see that the only parameter in the problem that has dimensions 1/T is ω₀ so we expect every Δt to come with an extra factor of ω₀. This is the case; so Δt must be small compared to 1/ω₀.

(c) The Taylor series expansion for sin θ is

So a good estimate for when the first term alone is off by 10% is

(Notice that we don't set the cubic term = 0.1. We are interested in a percentage change compared to the first term alone, therefore we have to consider the ratio of sin θ / θ which has the expansion in parentheses.)

RETURNS

University of Maryland	Physics Department	Physics 374 Home

Last revision 9. November, 2005.